INTRODUCTION

Since the 18^th century, when the projection theory and the descriptive geometry were introduced and used to solve engineering problems, 2D drawings were established in engineering design processes (Jeon et al., 2016; Lee and Han, 2005). Multi-view 2D drawings are not just a powerful presentation of the 3D object but a standard environment between design and manufacturing (Wen et al., 2015) as well and are sometimes used as the principal element showing the production and assembling process (Lee and Han, 2005; Wen et al., 2017a, 2017b). In today's societies, due to the limited resources of energy and so the need to quick production processes, the use of automatic systems is necessary (Banapurmath et al., 2018). It also leads to sustainable development that is essential for the modern economy (Elnashaie et al., 2018). In general, an accurate estimation of the geometric condition of the system can lead to a better understanding of the system's behavior and to prevent its possible and potentially harmful effects (Haghshenas et al., 2018; Jianu and Rosen, 2017; Shahriari et al., 2018). Most contemporary products are described using 2D drawings (Wang and Grinstein, 1993), however, since revising older product designs is a necessity, there are some unavoidable limitations to this type of drawing, some of which are as follows:

• Visualization in the form of 3D objects and the direct use of a 2D drawing without having its physical model is extremely difficult (Gorgani, 2016a);

• 2D drawings cannot be used as input for today’s manufacturing systems, and applications such as the analysis and prototyping are extremely difficult for them (Wang and Latif, 2007);

• Revision of 2D drawings is extremely time and cost consuming (Bai et al., 2010).

Given the above limitations, obtaining 3D models from 2D drawings becomes very important (Biasotti et al., 2016; Lahner et al., 2016). Obtaining 2D orthographic views form 3D models is a movement from high-level information to low-level information, and it is an easy procedure; however, since reconstructing 3D models from orthographic views is a movement from low-level information to high-level information, it is an extremely difficult task (Mura et al., 2016; Mura et al., 2014; Ochmann et al., 2016; Stephan and Cordy, 2013) . Such problems become more apparent when we start to realize that a lot of information is lost in the process of obtaining orthographic views from 3D models. Methods presented to reconstruct 3D models from 2D orthographic views can be categorized as follows:

• The B-Rep method (Boundary representation) (Bezdek, 1994; Shin and Shin, 1998; Soni and Gurumoorthy, 2003);

• The CSG method (Constructive Solid Geometry) (Aldefeld, 1983).

The B-Rep method was started by Ideas and continued to develop by others (Sakurai and Gossard, 1983). This method, which is a bottom-up method, can be described by the following steps (Sakurai and Gossard, 1983):

1. Transforming 2D vertices into 3D vertices;

2. Creating 3D line segments from 3D vertices;

3. Creating faces from 3D line segments;

4. Making 3D objects from faces.

The CSG method, a top-down method started by Aldefeld (1983), can also be explained as follows:

1. Obtaining 3D primary volumes from 2D drawings;

2. Performing Boolean operations on 3D primitives and identifying their participation;

3. Creating 3D solid as the final object.

While both of the above methods have good efficiency, they have serious problems as well. Compared with CSG, the B-Rep method encompasses a wider range of shapes but cannot analyze complicated ones and encounters some uncertainties (Geng et al., 2002). Since it uses Boolean operations, CSG is more efficient in presenting unique solutions (López-Sastre et al., 2013). However, since it uses basic primary shapes to reconstruct 3D objects, it has serious limitations when dealing with complicated shapes.

In both methods, the most serious problem occurs when we want to correlate elements in two different orthographic views (Jiang and Fu, 2011; Su et al., 2013). In fact, this problem appears when there is uncertainty and we need expert opinion and knowledge (Haghshenas et al., 2018; Wang et al., 2013). One of the most important applications of the fuzzy logic theory as a mathematical method is to correlate vague data sets by making use of expert knowledge (Ross, 2009). This theory was first introduced in 1965 by Professor L. A. Zadeh (1965) and has since become a link between humans and computers, which helps to minimize conflicts in this relation (Dubois and Prade, 1993). Based on this theory, factors and ranges can be categorized without having any precise boundary. The fuzzy logic theory is very useful for solving real-world problems. Vague variables and their impact on the system are called ‘psycho-linguistic variables’. This theory can thus be used in various fields such as calculus, topology, the humanities, experimental sciences, engineering, and, in general, wherever expert knowledge is needed (Dubois and Prade, 1993; Gorgani et al., 2017).

In this paper, first, two orthographic views are collated. Using the surface analysis method, two different orthographic views of the two-dimensional object are interconnected. This method is, in fact, a mathematical method based on expert knowledge and is thus precise and flexible. Furthermore, in case 2D engineering drawings are scratched, this method can offer an approximate model for the 3D object. Another advantage is that only two orthographic views are used to reconstruct the 3D model while in methods presented so far, 3 orthographic views have been used. So, we can claim that “the degree of ideality” of our system has improved (Gorgani, 2016b).

One of the limitations of this method, however, is that it can be applied only to models with planar faces and does not include curved faces.

EXPERT KNOWLEDGE: INTRODUCTION TO SURFACE ANALYSIS

The first and most difficult stage in the reconstruction of a three-dimensional object from two-dimensional orthographic views is to find the equivalent components in different views. To do this, we use the surface analysis method (Mottaghipour et al., 2018; Mottaghipour et al., 2017), described with an example as follows:

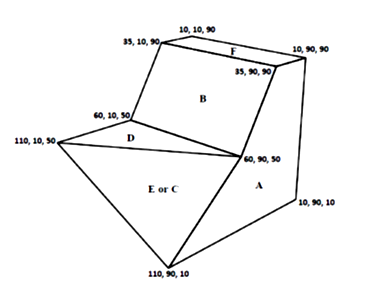
Consider polygon B in the 3D object as shown in Figure 1. Now, look at Figure 2, which includes front and top views of this object. In the top view, polygon B is seen as a polygon, while it appears as a line in the front view. Now, let us examine the features that this line has. As we can see from Figure 2, if we consider every corner of the polygon B in the top view, we can find an intersection with other components on the equivalent line in the front view and along with it. Of course, as shown in Figure 2, this correspondence is not one-to-one and 2 or more corners of the polygon may be related with a single intersection point on the line. The same is true for polygons C and E and their equivalent lines in Figure 2.

 

Figure 1. Sample 3-D object

 

Figure 2. A polygon that is equivalent to a line

 

Figure 3. A polygon that is equivalent to a polygon

 

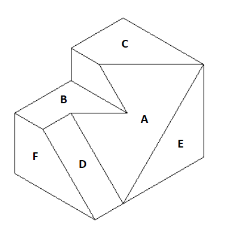
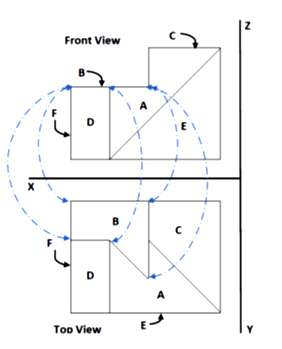
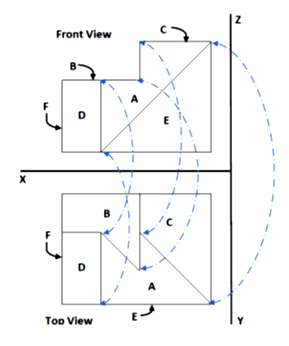
Now, consider polygon A in the 3D object shown in Figure 1. As Figure 3 shows, polygon A is seen as a polygon in the front view. It also appears as a polygon in the top view. Examining the properties of these polygons shows that there is a one-to-one correspondence between aligned corners of these two polygons. The same relationship can be seen between the front and top views of polygon D. The result can thus be expressed as follows:

If we consider a polygon in an orthographic view of a three-dimensional object, it can be equivalent to a single line or a polygon in another orthographic view. What is meant by "being equivalent" is that both of them are different orthographic views of a single polygon. If the equivalent image is a polygon, it is necessary to have a one-to-one correspondence between the corners of this polygon and the first polygon corners. If, on the other hand, the equivalent image is a line, there must be an intersection point on the line in the direction of each of the first polygon corners. (This correspondence is not necessarily one-to-one, of course). Now, using this principle, we will create the necessary formulas and fuzzy rules in the proposed method.

DEFINITION OF VARIABLES AND ALGEBRAIC PHRASES

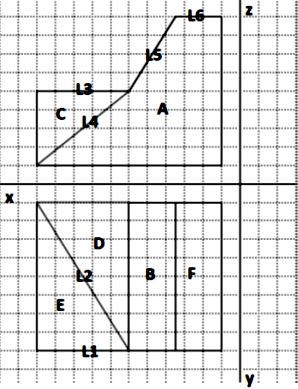
To explain this issue, we can start with an example. We are looking for an equivalent element for polygon “A” in Figure 4. All divisions are 10 mm × 10 mm squares. As mentioned earlier, first, we look for an equivalent polygon, polygon “B” for instance. The coordinates of all corners of polygon “A” stand in matrix \(A\) and the coordinates of all corners of polygon “B” stand in matrix \(B\). To do this, the coordinate that is related to the common axis, stand in the first column and the other stand in the second column:

\[A = \begin{bmatrix} 35 & 90 \\ 10 & 90 \\ 10 & 10 \\ 110 & 10 \\ 60 & 50 \\ \end{bmatrix},B = \begin{bmatrix} 60 & 10 \\ 35 & 10 \\ 35 & 90 \\ 60 & 90 \\ \end{bmatrix}\]

 

Figure 4. Sample 2D orthographic view

 

If matrix \(A\) is \(m \times n\) and matrix \(B\) is \(k \times l\), we can define matrix \(\text{Differ}\) as follows (See Eq.1):

\[Differ = \begin{bmatrix} \left| a_{11} - b_{11} \right| & \cdots & \left| a_{n1} - b_{11} \right| \\ \vdots & \ddots & \vdots \\ \left| a_{11} - b_{k1} \right| & \cdots & \left| a_{n1} - b_{k1} \right| \\ \end{bmatrix}\]

(1)

So, for matrices \(A\) and \(B\) in our example, we have:

\[Differ = \begin{bmatrix} 25 & 50 & 50 & 50 & 0 \\ 0 & 25 & 25 & 75 & 25 \\ 0 & 25 & 25 & 75 & 25 \\ 25 & 50 & 50 & 50 & 0 \\ \end{bmatrix}\]

Here, the first column of \(\text{Differ}\) shows the difference of common axis coordinate between the first point of \(A\) and each point of \(B\). Our purpose is to find out which point of \(B\) has the minimum difference with the first point of \(A\). Therefore, we generate matrix \(\text{MinDifferAB}\) which contains minimums of each column of \(\text{Differ}\). However, if, for example, in column 1, the minimum occurs in row 1, in other columns we are not allowed to get row 1 as the minimum; and if the number of columns is greater than the number of rows for columns that do not have any row to obtain as the minimum, we can get 2×(maximum of matrix \(\text{Differ}\)) as the minimum. The reason is that it shows the first polygon has more corners from the second polygon, which is a negative score for their conformity. We call this “the penalty method”. Therefore, in our example, we have:

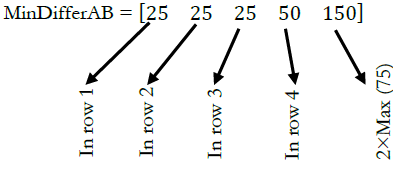
Now, if \(\text{MinDifferAB}\) is \(1 \times n\), \(\text{SumAB}\) is defined as follows:

\[SumAB = \sum_{i = 1}^{n}\text{MinDifferAB}_{1i}\]

(2)

which for our example will be:

\[SumAB = 25 + 25 + 25 + 50 + 150 = 275.\]

We then repeat the above process for case \(\text{BA}\) (polygon \(B\) as the first polygon and polygon \(A\) as the equivalent element). So we will have:

\[Differ = \begin{bmatrix} 25 & 0 & 0 & 25 \\ 50 & 25 & 25 & 50 \\ 50 & 25 & 25 & 50 \\ 50 & 75 & 75 & 50 \\ 0 & 25 & 25 & 0 \\ \end{bmatrix},MinDifferBA = \begin{bmatrix} 0 & 0 & 25 & 50 \\ \end{bmatrix},SumBA = 0 + 0 + 25 + 50 = 75.\]

Now, if \(\text{MinDifferAB}\) is \(1 \times n\) and \(\text{MinDifferBA}\) is \(1 \times l\), we define \(\text{FinalDiff}\) as follows:

\[FinalDiff = \frac{\max\left( SumAB,SumBA \right)}{\max\left\{ \left( n \times \max\left( \text{MinDifferAB} \right) \right),\left( l \times \max\left( \text{MinDifferBA} \right) \right) \right\}}\]

(3)

So, in the mentioned example, we have:

\[FinalDiff = \frac{\max{(275,75)}}{\max\left\{ \left( 5 \times 150 \right),\left( 4 \times 75 \right) \right\}} = \frac{275}{750} = 0.367\]

\(\text{FinalDiff}\) shows how much difference exists between two polygons after collating the nearest points together, because of the penalty method, the existence of an additional point in each polygon is considered a drawback in \(\text{FinalDiff}\). It is clear that \(\text{FinalDiff}\) is a number between 0 and 1 and if it is near 0, the possibility of conformity between the two polygons is greater. This variable is, therefore, a scale to check the first and second properties mentioned in the surface analysis.

After that, it is necessary to check the third property, i.e. the parallelism of two lines in equivalent polygons. If we show the number of the parallel line pairs of polygon “A” by \(\text{ParA}\) and the parallel line pairs of polygon “B” by \(\text{ParB}\), \(\text{ParDiff}\) can be defined as follows:

\[ParDiff = \left\{ \begin{matrix} \frac{\left| ParA - ParB \right|}{Max(ParA,ParB)} & \text{for max}(ParA,ParB) \neq 0 \\ 0 & \text{for max}\left( ParA,ParB \right) = 0 \\ \end{matrix} \right.\ \]

(4)

It is clear that, \(\text{ParDiff}\) is a number between 0 and 1 and in case it is closer to 0, it signifies better conformity between the two polygons. In our example, for polygons “A” and “B” we have:

\[ParA = 1,\ ParB = 2ParDiff = \frac{\left| 1 - 2 \right|}{2} = 0.5\]

After analyzing the conformity of the two polygons, we then present a method to find out the conformity of one polygon with a line. This method is greatly similar to the other method with the difference that in matrix \(B\), we substitute corners of polygon “B” with the intersection points on the noted line. For example, if we note line \(L1\) as the equivalent element for polygon “A”, we will have:

\[C = \begin{bmatrix} 110 & 50 \\ 110 & 10 \\ 60 & 50 \\ \end{bmatrix},L1 = \begin{bmatrix} 110 & 90 \\ 60 & 90 \\ \begin{matrix} 35 \\ 10 \\ \end{matrix} & \begin{matrix} 90 \\ 90 \\ \end{matrix} \\ \end{bmatrix}\]

Then, same as the other method, we generate matrix \(\text{Differ}\) as follows:

\[Differ = \begin{bmatrix} 0 & 0 & 50 \\ 50 & 50 & 0 \\ \begin{matrix} 75 \\ 100 \\ \end{matrix} & \begin{matrix} 75 \\ 100 \\ \end{matrix} & \begin{matrix} 25 \\ 50 \\ \end{matrix} \\ \end{bmatrix}\]

Now, we generate \(\text{MinDifferAB}\) the same way as the other method but here, recurrence of the rows is permitted. The penalty method, however, is not used here since one intersection point can be equivalent to more than one corner. So, we have:

\[MinDifferAB = \begin{bmatrix} 0 & 0 & 0 \\ \end{bmatrix},SumAB = 0 + 0 + 0 = 0\]

Another difference with the other method is that here we do not perform the reverse process for the line as the first element and the polygon as the equivalent and \(\text{MinDifferBA}\) is, therefore, not calculated. Hence, if \(\text{MinDifferAB}\) is \(1 \times n\), for \(\text{FinalDiff}\) we have:

\[FinalDiff = \left\{ \begin{matrix} \frac{\text{SumAB}}{n \times Max(MinDifferAB)} & \text{for max}(MinDifferAB) \neq 0 \\ 0 & \text{for max}\left( \text{MinDifferAB} \right) = 0 \\ \end{matrix} \right.\ \]

(5)

So, for polygon \(C\) and line \(L1\), we have:

\[FinalDiff = 0.\]

As we know from expert knowledge, against each corner of the polygon, there should be an intersection point over the equivalent line. If such a point exists for corner number i, there is a zero in column i of matrix \(\text{Differ}\). So, the number of columns of matrix \(\text{Differ}\) which does not have any zero value is the number of corners of the polygon without any equivalent intersection point over the line. We can define variable \(\text{SingCor}\) as follows:

\[SingCor = \frac{Number\ of\ columns\ without\ zero\ value\ in\ matrix\ Differ1}{Max(Number\ of\ vertices\ of\ polygon,Number\ of\ intersection\ points\ over\ line)}\]

(6)

So in our example for polygon \(C\) and line \(L1\) we have:

\[SingCor = \frac{0}{4} = 0.\]

It is clear that \(\text{SingCor}\) is a number between 0 and 1 and in case it is closer to 0, the conformity of the polygon and the line is better.

FUZZY VARIABLES AND MEMBERSHIP FUNCTIONS

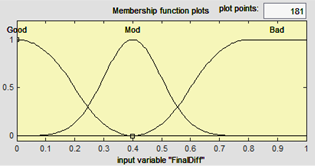
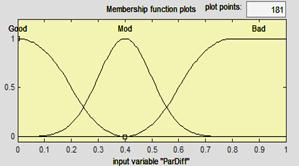
As we saw above, there are two types of conformity: conformity of the polygon with polygon and conformity of the polygon with line. For the first type of conformity, input variables of the fuzzy structure are defined as Figure 5 and Figure 6.

 

Figure 5. Membership functions of FinalDiff

 

Figure 6. Membership functions of ParDiff

 

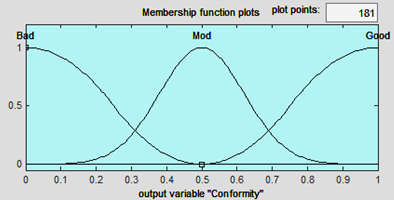
Also, for the output variable called conformity, we have membership functions as Figure 7.

 

Figure 7. Membership functions of conformity

 

Like before, for the second type of conformity, input variables of the fuzzy structure are defined as Figure 8 and Figure 9 and for the output variable called conformity, we have membership functions as Figure 10.

 

Figure 8. Membership functions of FinalDiff

 

Figure 9. Membership functions of SingCor

 

Figure 10. Membership functions of conformity

 

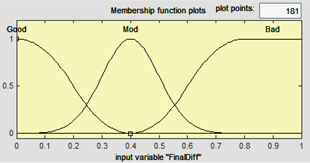
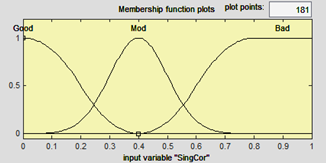
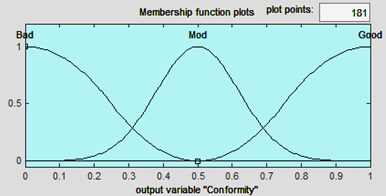
For all input variables, the membership function for type “bad” is SMF, for type “good” is ZMF, and for type “mod” is Gaussian. On the other hand, for all output variables, the membership function for type “bad” is ZMF, for type “good” is SMF, and for type “mod” is Gaussian. It should be noted that these membership functions are not necessarily unique and a special good membership function with a different form can be defined with the user, based on his/her knowledge and experience.

FUZZY CONTROL RULES

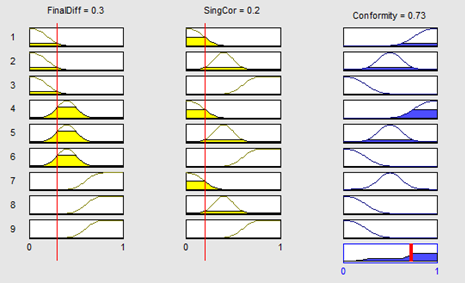
In general, the correlation between fuzzy variables is established by the use of “if-then” expressions based on expert knowledge, called “fuzzy rules”. The modality of fuzzy inference in these rules can be either the “Mamdani” type or the “Sugeno” type. In Mamdani type, Output membership function is present, crisp result is obtained through de-fuzzification of rules’ consequent, has non-continuous output surface, contains MISO (Multiple Input Single Output) and MIMO (Multiple Input Multiple Output) systems, has expressive power and interpretable rule consequents and has less flexibility in system design. In the other side, in Sugeno type, No output membership function is present, No de-fuzzification: crisp result is obtained using weighted average of the rules’ consequent, there is continuous output surface, only MISO systems covered, we encounter loss of interpretability but more flexibility in system design. So, Mamdani FIS is well suited to human input while Sugeno FIS is well suited to mathematically analysis. Here, based on system properties, the “Mamdani” type is selected. Fuzzy rules for polygon-polygon conformity are as follows:

1. If FinallDiff is bad AND Pardiff is bad, THEN Conformity is bad. (Weighted: 1)

2. If FinallDiff is bad AND Pardiff is mod, THEN Conformity is bad. (Weighted: 1)

3. If FinallDiff is bad AND Pardiff is good, THEN Conformity is mod. (Weighted: 0.5)

4. If FinallDiff is mod AND Pardiff is bad, THEN Conformity is bad. (Weighted: 1)

5. If FinallDiff is mod AND Pardiff is mod, THEN Conformity is mod. (Weighted: 1)

6. If FinallDiff is mod AND Pardiff is good, THEN Conformity is good. (Weighted: 0.5)

7. If FinallDiff is good AND Pardiff is bad, THEN Conformity is bad. (Weighted: 0.5)

8. If FinallDiff is good AND Pardiff is mod, THEN Conformity is mod. (Weighted: 0.5)

9. If FinallDiff is good AND Pardiff is good, THEN Conformity is good. (Weighted: 1)

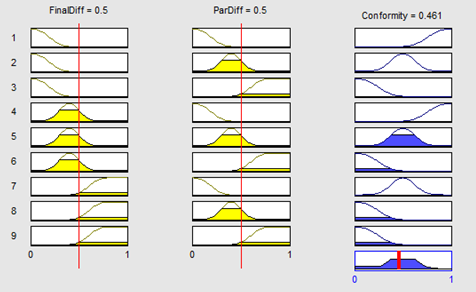
Figure 11 shows the graphical interpretation of this fuzzy system which is modeled using the MATLAB fuzzy toolbox. Each rule is shown in one row of the graphical diagram and each variable is set in one column. The first two columns show the “if” part of fuzzy rules, i.e. input variables, and the third column shows the “then” part or the output variable.

 

Figure 11. Graphical interpretation of fuzzy rules for polygon-polygon conformity

 

Also, detected fuzzy rules for adaptation of the polygon and line are as follows:

1. If FinallDiff is good AND SingCor is good, THEN Conformity is good. (Weighted: 1)

2. If FinallDiff is good AND SingCor is mod, THEN Conformity is mod. (Weighted: 1)

3. If FinallDiff is good AND SingCor is bad, THEN Conformity is bad. (Weighted: 1)

4. If FinallDiff is mod AND SingCor is good, THEN Conformity is good. (Weighted: 1)

5. If FinallDiff is mod AND SingCor is mod, THEN Conformity is mod. (Weighted: 1)

6. If FinallDiff is mod AND SingCor is bad, THEN Conformity is bad. (Weighted: 1)

7. If FinallDiff is bad AND SingCor is good, THEN Conformity is mod. (Weighted: 1)

8. If FinallDiff is bad AND SingCor is mod, THEN Conformity is bad. (Weighted: 1)

9. If FinallDiff is bad AND SingCor is bad, THEN Conformity is bad. (Weighted: 1)

CORRELATION OF ELEMENTS IN DIFFERENT ORTHOGRAPHIC VIEWS

In Figure 4, front and top views of an object are given. In the front view, we have polygons A, C and in the top view, we have polygons B, D, E, F. Therefore, we have 2×4=8 forms of conformity between these polygons for which FinalDiff and Pardiff are calculated and shown in Table 1. Then, based on the mentioned fuzzy system, conformity is evaluated for each state.

 

Figure 12. Graphical interpretation of fuzzy rules for polygon-line conformity

 

Table 1. Evaluated values for polygon-polygon adaptation No. 1st Polygon 2nd Polygon FinalDiff ParDiff Conformity 1 A B 0.3667 0.5 0.461 2 A D 0.5750 1.0 0.178 3 A E 0.6250 1.0 0.162 4 A F 0.2750 0.5 0.454 5 C B 0.5000 1.0 0.162 6 C D 0.3333 0.0 0.822 7 C E 0.0000 0.0 0.857 8 C F 0.5313 1.0 0.175

 

After that, we analyze polygon-line conformity. In Figure 4 in the front view, there are lines L3, L4, L5, and L6 and in the top view, there are lines L1, L2. Thus, for the front view polygons we have 2×2=4 conformity forms and for the top view polygons, we have 4×4=16 forms. As before, for all these states, variables FinalDiff, SingCor are calculated and then, using the fuzzy model, the conformity is evaluated and displayed in Table 2.

 

Table 2. Evaluated values for polygon-line adaptation No. Polygon Line FinalDiff SingCor Conformity 1 A L1 0.0000 0.0000 0.857 2 A L2 0.5000 0.6000 0.270 3 C L1 0.0000 0.0000 0.857 4 C L2 0.0000 0.0000 0.857 5 B L3 0.5000 0.5000 0.461 6 B L4 0.5000 0.5000 0.461 7 B L5 0.0000 0.0000 0.857 8 B L6 0.5000 0.5000 0.461 9 D L3 0.0000 0.0000 0.857 10 D L4 0.0000 0.0000 0.857 11 D L5 0.3333 0.3333 0.514 12 D L6 0.5556 1.0000 0.185 13 E L3 0.0000 0.0000 0.857 14 E L4 0.0000 0.0000 0.857 15 E L5 0.6667 0.6667 0.176 16 E L6 0.7778 1.0000 0.143 17 F L3 0.7500 1.0000 0.144 18 F L4 0.7500 1.0000 0.144 19 F L5 0.5000 0.5000 0.461 20 F L6 0.0000 0.0000 0.857

 

As for Table 1, and evaluated conformity numbers for each state, we can see that all of the conformities have low values except C-D and C-E adaptations. However, C-E adaptation value is greater and, consequently, we can conclude that C and E are equivalent.

Table 2 shows that line L1 is an equivalent of polygon A. Both L1 and L2 can be equivalents of polygon C, however, since we identified an equivalent element for polygon C (polygon E) before, we can ignore these states. Also, line L5 is an equivalent of polygon B and L6 is an equivalent of F. For polygon D, both lines L3 and L4 can be the equivalent element and we will spot both in the reconstruction of the 3D object.

 

RECONSTRUCTION OF THE 3D OBJECT

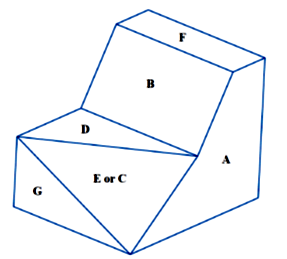
Based on the results of Tables 1 and 2 and as the x-axis is the common axis between the two views, it is sufficient to collate points in equivalent elements and obtain 3D coordinates of each point. Results are shown in Table 3.Now, we locate the points of Table 3 in the 3D state. Figure 13 is obtained. The lower left corner of the 3D object is empty and based on the two given orthographic views, the noted region is a straight line in views, so, as a simple solution, it can be a polygon such as “G”. Also, in the hidden regions of this object, we can simply state a polygon and the completed 3D object will be similar to Figure 14.

 

Table 3. 3D coordinates of points in orthographic views No. Equivalent elements 3D points 1 A and L1 (110, 90, 10) , (60, 90, 50) , (35, 90, 90) , (10, 90, 90) , (10, 90, 10) 2 C and E (110, 10, 50) , (110, 90, 10) , (60, 90, 50) 3 B and L5 (60, 10, 50) , (60, 90, 50) , (35, 10, 90) , (35, 90, 90) 4 F and L6 (35, 10, 90) , (10, 10, 90) , (35, 90, 90) , (10, 90, 90) 5 D and L3 (110, 10, 50) , (60, 10, 50) , (60, 90, 50) 6 D and L4 (110, 10, 10) , (60, 10, 50) , (60, 90, 50)

 

Figure 13. Resulted 3D object from Table 3

 

Figure 14. Resulted final 3D objects

 

IMPACT OF 3D RECONSTRUCTION ON SUSTAINABLE DEVELOPMENT INDICATORS

The term “sustainable development” has several definitions. For example, one of the most common definitions is the definition given by Brundtland Commission in 1987 as following (Rosen, 2017):

“Development that meets the needs of the present without compromising the ability of future generations to meet their own needs.”

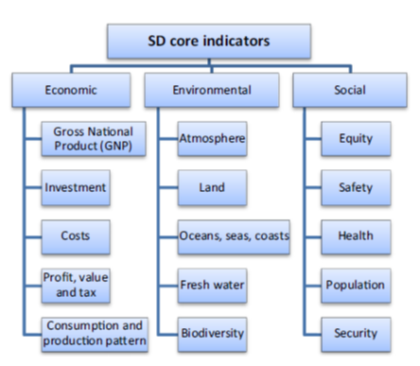
A review of papers suggests that sustainable development indicators are divided into three main categories: social, environmental and economic (Hatakeyama, 2018; Seyajah et al., 2014; Shaaban and Scheffran, 2017) and each category contains several sub-indicators as an example is shown in Figure 15.

 

Figure 15. Sustainable development indicators core indicators and sub-indicators (Shaaban and Scheffran, 2017)

 

On the other hand, the review of 3D modeling applications suggests that many of these applications can be effective on sustainable development indicators. Obviously, the scope of this effect can range from very low to very high values. To study this, an influence matrix is formed as Table 4. In this matrix, 3D modeling applications are arranged as E1 to E9 and some of sustainable development indicators (which can be affected by E1 to E9) arranged as C1 to C8. The intersection of row i and column j, briefly EiCj, represents the effect of the application Ei on indicator Cj. The intensity of this effect is divided into six categories which are characterized by linguistic fuzzy variables: No effect (N), Very Low effect (VL), Low effect (L), Moderate effect (M), High effect (H) and Very High effect (VH). In the following, some of these effects are explained:

Better Visualization using 3D Object (E1) improves spatial visualization and spatial intelligence, it can be very influential on education in disciplines such as engineering and design, improve the quality of education and save time and money. It can also improve the health level through the improvement of the 3D model of the components, lesions and internal damages of the body .Performing Finite Element Analyzes on 3D Model (E2) such as Static, Dynamic, Thermal, Ergonomic & etc. can reduce the design time and provide the possibility of optimization, which results in lowering the cost and reducing the risk of investment and increasing the incentive for investment.

Otherwise, as well as the risk reduces, the use of new energy and recyclable materials increases that can protect energy resources and forests. On the other hand, it can make it easier to educate engineering courses. As another example, Simulation of Production Processes on a 3D Model (E4), can optimize the production line, reduce the risk of investing in production, and preventing energy waste. Also, keeping the drawings in the computer's memory, on one side, can reduce the need for printing and thus reduce the consumption of paper, which is very effective at cost and protecting the trees.

 

Table 4. 3D Reconstruction vs. Sustainable Development Sustainable Development       3D Reconstruction Sustainable Development Indicators Economic Environmental Social Cost Investment Energy Consumption Renewable Materials Forests Protection Education Health Security Description Code C1 C2 C3 C4 C5 C6 C7 C8 Better Visualization using 3D Object E1 M M L L L VH VH N Performing Finite Element Analyzes on 3D Model E2 H H H H H M H N More Speed in Design E3 H L M N N N N M Simulation of Production Processes on a 3D Model E4 VH H H M L L N N Maintaining Drawings in Computer Memory E5 N N N N VH N N VH Need a Lower Level of Skill for the Operator E6 M L L N N VH L L Simpler Standardization and Synchronization E7 H L M N N H N N Direct Connection to CAD/CAM Systems E8 VH L M N N L N M Using Fuzzy Inference E9 N N N N N H N N

 

CONCLUSION

This paper presents a method to reconstruct 3D objects from two orthographic views and solves the weakness of some former methods including the uncertainty in correlating elements in orthographic views by the use of the fuzzy logic theory. Some of the advantages of this method are as follows:

• All previous methods use 3 orthographic views to reconstruct 3D objects but this method uses only 2 views.

• By making use of the fuzzy logic, this method has a high level of flexibility and can resolve vagueness and uncertainty.

• This method is based on expert knowledge, so there is very low possibility of the absolutism of computer systems.

• Since this method presents different possibilities for each adaptation state, it can be used to reconstruct final 3D objects of scratched engineering drawings.

Meanwhile, a limitation of this method is that it can only be applied to planar faces and does not include curved surfaces. In future research, it is suggested that its scope should be broadened to involve curved surfaces.

On the other hand, increasing the possibility of reconstruction of 3D Objects from 2D orthographic views will result lower cost, lower investment risk, reduced energy consumption, increased use of renewable materials, conservation of natural resources, improved education quality and increased health level, all of which means creating sustainable development in three areas: economic, social, and environmental.