INTRODUCTION

Due to the concerns associated with greenhouse gas emissions and the resulting global warming, there is a global trend towards more sustainable and clean energy sources. Alternative sources for coal and other fossil fuels are nuclear power and renewable energy with wind energy being one of the most promising source. However, public acceptability often poses a barrier towards renewable energy development and one of the concerns with wind turbine technology pertains to the noise that they produce during operation. In order to successfully reduce or prevent the noise generated, the first step is to identify the sources of noise. The two major sources of noise identified during operation are mechanical and aerodynamic (Klug, 2002). Mechanical noise generally originates from the mechanical components within the wind turbine due to friction and vibration. The generator, the hydraulic systems and the gearbox are the main sources of mechanical noise. The major source of noise in wind turbines is the aerodynamic noise due to the fluid-structure interaction. It has been identified that the largest contributor to aerodynamic noise is generated in the trailing edge of wind turbine blades (Klug, 2002). Since the exergy destruction characterizes losses in energy or usefulness of the system, it can be employed to describe loses due to noise generation so that prevention methods can be found. Hence, the research team conducted a study to model the noise generated in terms of exergy destruction: a useful quantity describing the mutual equilibrium of a system and its surroundings. It has been found that in order to increase system’s usefulness and ultimately decrease the noise generated, exergy destruction must be reduced.

This paper is organized as follows: noise sources and prevention are discussed in second section, exergy methods are discussed in third section, approach and methodology are discussed in forth section, analysis is introduced in fifth section, sixth section presents the results and discussion and conclusions are given in last section. Approach and methodology section is subdivided into correlating sound pressure level (SPL) to exergy destruction and methodology. Results and discussion section is subdivided into SPL, correlation development and needs and limitations.

NOISE SOURCES AND PREVENTION

The noise disturbances by wind turbines are related to such factors as distance between the wind turbine and populated areas as well as the background noise where the wind turbine is operating. Operating conditions and maintenance of the wind turbine also affect noise production, in particular the noise produced by the mechanical components, which is more tonal. Noise produced by mechanical components tends to be more tonal in nature and it was found that it is more irritating for humans than broadband sound (Klug, 2002). Mechanical noise can be airborne or transmitted via structure (Romero-Sanz and Matesanz, 2008). Noise that is airborne is straightforward since the sound is emitted to the surroundings without interfering with other structures. Structural noise is harder to detect and analyze as it is usually created in the mechanical components, amplified along the structure of the turbine and then emitted into the surroundings through the casing, the nacelle cover, and the rotor blades. Nonetheless, mechanical noise is not as complex as aerodynamic noise - the dominant source of noise from wind turbines (Romero-Sanz and Matesanz, 2008).

Generally, six main regions have been identified along the blades of wind turbines, which are classified into turbulent boundary layer trailing edge (TBL-TE) noise, laminar boundary layer vortex shedding (LBL-VS) noise, separation stall noise, trailing edge bluntness vortex shedding noise, tip vortex formation noise and noise due to turbulent inflow (Klug, 2002; Romero-Sanz and Matesanz, 2008; Oerlemans et al., 2007; Moriarty and Migliore, 2003; Schepers et al., 2007; Brooks et al., 1989; Leloudas et al., 2007; Oerlemans and Schepers, 2009; Jianu et al., 2012). As such, scientists developed methods to predict the noise generated within these regions. One such predictor for TBL-TE was developed by Brooks and Hodgson (1981). This predictor measures surface pressures and outputs the level of noise generated. Another method based on the surface pressures was developed by Schlinker and Amiet (1981). In their study they are predicting the noise based on a generalized empirical formula for surface pressures rather than the measured quantity. A simpler approach to the TBL-TE which is based on an edge-scatter formulation, was presented by Ffowcs and Hall (1970). Studies also show that the TBL-TE is influenced by the Reynolds number and angle of attack (Schlinker and Amiet, 1981; Ffowcs and Hall, 1970; Chou and George, 1984). Additionally, it has been found that trailing edge noise is generated when the flow is mildly separated whereas for large-scale separation, noise is transmitted from the chord. This has been determined through far-field cross correlations (Chou and George, 1984). Of great interest is the LBL-VS noise as it can be combined to acoustically excited feedback loops. These are found between the trailing edge and instability waves (i.e. Tolmien-Schlichting waves) upstream of the trailing edge (Brooks et al., 1989; Leloudas et al., 2007; Paterson et al., 1974, George et al., 1980, Arakawa et al., 2005; Tam, 1974; Fink, 1978; Wright, 1976). To predict the tip vortex formation, Brooks, Pope and Marcolini developed a relation for an untwisted, constant chord blade (Brooks et al., 1989; Ffowcs and Hall, 1970; Brooks and Marcolini, 1986). Empirical relations for turbulent inflow noise were developed by Lowson (1992) based on the experimental results of Amiet (1975). These relations apply to both low and high frequencies.

Sound generation can be prevented or reduced using different techniques. The simplest method is to consider the acoustic behavior of the wind turbine in its design. However, the main focus of researchers is to minimize the noise generated by the turbine while maximizing its power generation. Some methods involve detecting noise in the mechanical components using artificial intelligence (Kelly, 2000; Wang et al., 2011; Angelov and Filev, 2004; Song and Kasabov, 2005; Kasabov and Song, 2002; Wang et al., 2004; Jianu, 2010) while others are focusing on blade designs and introducing serrations to minimize the aerodynamic noise (Oerlemans et al., 2001; Oerlemans, 2008; Kamruzzaman et al., 2012; Herr, 2006). In this study the authors are applying a factor not generally used to design wind turbine airfoils with the intention of minimizing noise pollution. Hence, the authors are attempting to relate sound to exergy. The correlation between the sound pressure level resulting from flow over an object and the exergy destroyed within the fluid medium has the potential to reveal useful information related to noise generation and aid in efforts to minimize noise pollution in commercial wind turbines.

EXERGY METHODS

Exergy destruction has been chosen for this analysis since friction of fluid over a surface is an irreversibility that generates entropy and anything that generates entropy always destroys exergy. For a 2-dimensional flow over an object, the exergy destroyed (Ex_d) can be found after performing an exergy balance over a plane. For this study, the plane is situated downstream of the fluid domain since the noise intensifies behind the airfoil. This is represented by (Li et al., 2006):

\(Ex_{d} = \int_{2}^{}{\rho u_{2}}\left\lbrack \left( h_{2} - h_{0} \right) - T_{0}\left( s_{2} - s_{0} \right) + \frac{u_{2}^{2} + v_{2}^{2}}{2} \right\rbrack dS - \int_{3}^{}{\rho u_{3}}\left\lbrack \left( h_{3} - h_{0} \right) - T_{0}\left( s_{3} - s_{0} \right) + \frac{u_{3}^{2} + v_{3}^{2}}{2} \right\rbrack\text{dS}\) (1)

where subscript 0 represents the environment, subscript 2 represents the entrance of the control surface and subscript 3 is the exit of the control surface; \(h_{i}\) and \(s_{i}\) are the enthalpies and entropies, respectively; \(T_{0}\) represents the temperature of the environment; \(u_{i}\) and \(v_{i}\) are the velocities in \(x\) and \(y\) direction, respectively and \(\rho\) represents the air’s density.

The following assumptions will be made about Eq. (1).

1. The properties of the fluid within the control volume are constant and therefore \(h_{0} = h_{2} = h_{3}\), \(s_{0} = s_{2} = s_{3}\)

2. The surface located behind the solid object (i.e. surface 3) is far enough from the object that it is approaching the velocity of the freestream, hence \(u_{3} \rightarrow\) ∪_∞, \(v_{3} \rightarrow 0\), \(x \rightarrow \infty\)

3. The control surface is wide enough that there is no flow through the boundaries other than the input and output boundaries. That is, the fluid flow is in one direction over the solid object from surface 2 towards surface 3.

4. The input and output surfaces equal in size.

After applying the above assumptions, Eq. 1 simplifies to the following form:

\(Ex_{d} = \int_{2}^{}{\rho\left( \frac{u_{2}^{3} - u_{\infty}^{3} + {u_{2}v}_{2}^{2}}{2} \right)}\) (2)

This expression will be used to calculate the exergy destruction in this analysis. A correlation between exergy destruction and sound pressure level (SPL) will then be obtained.

APPROACH AND METHODOLOGY

The approach in this analysis focuses on determining a correlation between the noise pollution and the exergy destroyed as a result of fluid flow over a cylindrical object using computational methods. This correlation has the potential to reveal the association between noise pollution and exergy destruction with the purpose of being used for noise pollution minimization while increasing efficiency in commercial wind turbines. As such, SPL is used to describe noise pollution and correlate it to \(Ex_{d}\). A fluid domain consisting of air is initially formulated to represent the structure of the problem. A solid object is then created and modeled in the center of the fluid domain, measured in the vertical axis and perpendicular to fluid flow. The fluid flow is modeled using the Navier-Stokes (N-S) equation whereas the acoustic sound pressure is modeled by the acoustic wave (AW) equation. Hence, these two equations are used to model the interaction of the two physical processes in this study. Since these equations have a pressure term describing them, they could be coupled. That is, the pressure term from the N-S equation was set equal to the pressure term in the AW equation. Since these equations share a mutual term, they were solved simultaneously using COMSOL Multiphysics. In this study, Eq. 2 is integrated over the boundary and the SPL is obtained using the software that allows for simulation of multiphysics. After simulating the flow over the object and generating the results, a relationship between the SPL and \(Ex_{d}\) as well are SPL and ∪_∞ was obtained. It was found that for both SPL vs. \(Ex_{d}\) and SPL vs. ∪_∞ the best approximation in that returned the lowers root mean square error (RMSE) was an exponential function of the form in Eq. 3 below:

\(f\left( x \right) = ax^{b}\) (3)

where \(a\) and \(b\) are constants to be determined from analysis.

The present study can be expanded to analyze sound pollution in wind turbines by analyzing the individual airfoils themselves. This is a problem of interest among today's researchers and is a work in progress.

ANALYSIS

Prior to simulating the model, an analysis was performed to determine the conditions under which the results are valid. These boundary conditions were previously used in literature (Zhu, 2007) and were determined to be as follows:

• Velocity at the inlet is normal to the control surface.

• Pressure at the outlet is atmospheric and no viscous stresses are present.

• The surfaces parallel to the flow of the fluid are assumed to be outlying the object and therefore no flow crosses the boundaries. This allows for the "wall" boundary condition to be applied.

• The inlet normal velocity, ∪_∞, ranges from 1.5 m/s to 9 m/s however, the results presented in the next section are for a velocity of 7 m/s. This value was chosen based on energy and exergy efficiency maps generated by Dincer and Rosen (2007).

RESULTS AND DISCUSSION

In this section, the results of the study are described and discussed according to the methodology and analysis described. First, the choice in SPL is justified; second, the results of the correlation are presented and lastly, the limitations of the study are discussed.

Sound Pressure Level

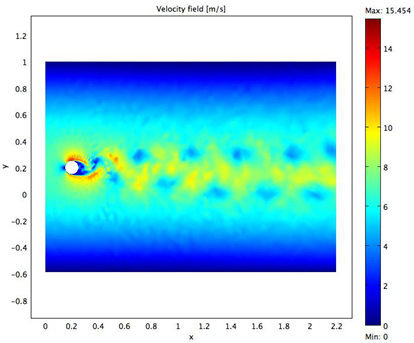
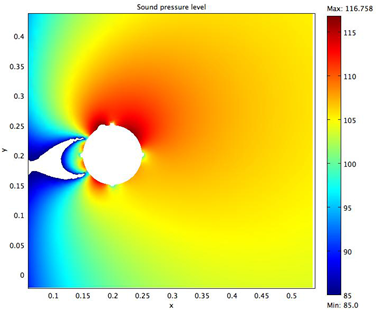
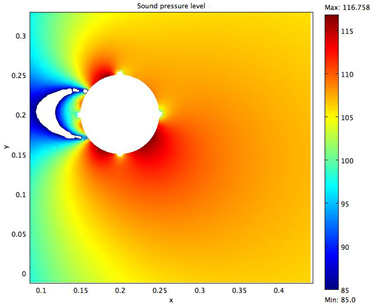
A time dependent domain was chosen to achieve the solution of the problem and ensure that any time dependent properties of the system, such as vortex shedding, are revealed. Vortex shedding in the wake of the solid object is an important physical attribute that generates pressure variations in the medium of the fluid, which consequently generate fluctuations in noise. Since a complicated mathematical model for which an analytical solution is challenging to obtain characterizes vortex shedding, Computational Fluid Dynamics (CFD) software is employed in order to determine a solution. In Figure 1 the formation of the pressure fluctuations and hence of the vortex can be observed clearly. It can be noted that the vortex is generated periodically with a counter-clockwise rotating vortex forming from the bottom of the object and the clockwise rotating vortex forming at the top of the solid object. The position of the vortices is almost equidistant along the horizontal distance, indicating a cycling nature of the vortex shedding behind the cylinder (Tomimatsu and Fujisawa, 2002). It is to be noted that the frequency of vortex shedding matches with the frequency of the fluctuation of the SPL. The SPL at t = 4.7 s can be observed in Figure 2. Note that the higher SPL is located at the top of the cylinder, while the location of higher intensity level is shifted to the bottom of the cylinder at t = 4.84 s. This phenomenon can be observed in Figure 3.

Figure 1. Velocity field and vortex shedding

Figure 2. Sound pressure level at t = 4.7 s.

Figure 3. Sound pressure level at t = 4.84 s.

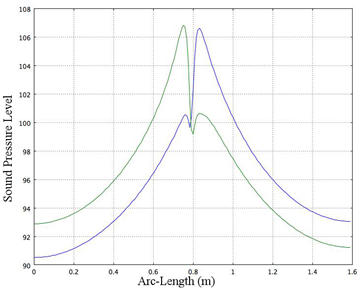
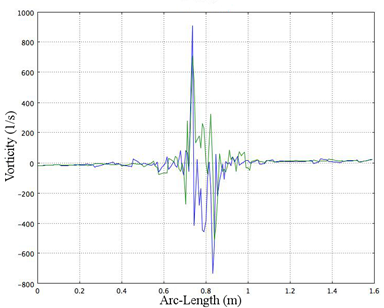
A cross section at x = 0.28 is analyzed in terms of the SPL, for two times: t = 4.7 s and t = 4.28 s. The results are plotted in Figure 4. A higher intensity level can be observed at y = 0.75 m, where y is the arc length. This intensity is associated with a time of t = 4.82 s and is represented by the green line on the plot. The blue line represents the SPL at a time of t = 4.7 s and it is noted that a change occurs in the variation of the sound pressure levels. The variations are almost mirror images of each other, indicative of pressure variations between the upper and lower half of the vortex shedding region.

Figure 4. Cross section of sound pressure level at t = 4.84 s (green) and t = 4.7 s (blue).

By observing the vorticity field in Figure 5, it can be concluded that the vorticity is also out of phase at those particular time steps. Therefore, the frequency of the vortex shedding coincides with the frequency of SPL variation.

Figure 5. Cross section of vorticity at t = 4.7 s (blue) and t = 4.84 s (green).

Correlation of Exergy Destruction with Sound Pressure Level

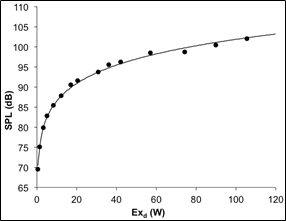
The scope of this study is to relate the SPL to \(Ex_{d}\) and since Eq. 2 tells us that\(\text{E}x_{d}\) is a function of the velocity, it is implied that \(Ex_{d}\) increases with the increase of SPL. It should be noted that Eq. 2 was employed to compute\(\text{E}x_{d}\) whereas the SPL was obtained from simulations. The SPL was then plotted as a function of \(Ex_{d}\) as shown in Figure 6 and the function assumes an exponential form given by Eq. 3. The constants \(a\) and \(b\) in Eq. 3 that return the best approximation between SPL and \(Ex_{d}\) were determined to be 73.5 and 0.07, respectively; hence the equation can be written as follows:

\(SPL = 73.5\left( Ex_{d} \right)^{0.07}\) (4)

This fit returned an R² value of 0.997 implying that the variables correlate very well. It can be noted from Eq. 4 and from Figure 6 that SPL is a positive function of \(Ex_{d}\) and SPL quickly increases for lower ∪_∞ with increasing \(Ex_{d}\). In this study ∪_∞ is increased in 0.5 increments from 1.5 to 9 m/s. Also, although \(Ex_{d}\) increases with an increase in velocity, the SPL converges to about 105 dB. This value is comparable to the SPL generated by flow over a wind turbine’s airfoil, which is about 102 dB (Jianu et al., 2012).

Figure 6. SPL vs. Ex_d curve fit.

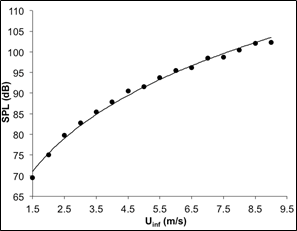
A similar relationship is obtained when expressing SPL in terms of ∪_∞. The constants \(a\) and \(b\) as shown in Eq. 3 are also determined and the exponential function obtained can be written as:

\(SPL = 65.2\left( U_{\infty} \right)^{0.21}\) (5)

Correspondingly, this approximation returned an R² value of 0.994 which also indicates a good relationship between the SPL and ∪_∞. The plot corresponding to the function is shown in Figure 7.

Figure 7. SPL vs. ∪_∞ curve fit.

Similarly to the previous findings, the SPL is a positive function of ∪_∞ and increases with an increase in ∪_∞. This behavior of the function was expected since \(Ex_{d}\) is also a function of ∪_∞. However, the function increases more gradually and the convergence is not as obvious as in the correlation between SPL and \(Ex_{d}\). This is attributed to the fact that \(Ex_{d}\) is not a linear function of velocity.

From the above findings it can be inferred that there is a positive correlation between the sound pressure level and the exergy destruction. For the lower values of exergy destruction it is shown that the noise is extremely affected by any increase in exergy destruction. Thus, with such a strong correlation between the two, one can suggest that by decreasing the exergy destruction, the noise generated will also be decreased.

Limitations and Needs

Simulations and mathematical models for 3-dimensional flow over a similar object will be performed and compared to other studies. These simulations will aid in the understanding of fluid structure interactions so that the method can be further applied to airfoils. The SPL produced when fluid interacts with airfoils in 2-D and 3-D will be investigated. The analysis will be performed for turbulent \(k - \varepsilon\) models and the correlation between SPL and \(Ex_{d}\) as well as SPL and ∪_∞ will be determined in order to optimize airfoil shape for noise reduction.

CONCLUSION

The main goal of this work was to establish a correlation resulting from fluid flowing over a solid object noise generation and the exergy destroyed within this fluid medium. The SPL produced as a result of flow over a two-dimensional cylindrical model was investigated. CFD simulations in COMSOL Multiphysics were performed in order to estimate the SPL, which was then related to \(Ex_{d}\) and ∪_∞. Relationships between SPL and,\(\text{E}x_{d}\), and SPL and ∪_∞ were determined and it was found that they both relate through exponential functions. Further investigation showed that although \(Ex_{d}\) increases with increasing velocity, the SPL has a terminal value of about 105 dB, which is similar to that of SPL resulting from flow over an airfoil. Hence, from the study it can be concluded that an increase in noise pollution should be expected as the exergy destruction increases.

ACKNOWLEDGEMENTS

The authors acknowledge the financial support from the Natural Sciences and Engineering Research Council of Canada.

CONFLICT OF INTEREST

The authors declare no conflict of interest.