Abstract
The objective of this paper is to study in which way the strategies to combat climate change, as prescribed in the UN SDG number 13, are influenced by ambiguity aversion. Countries can tailor the UN SDGs to their priorities and situations, but the urgency in their planned actions to combat climate change and its impact is affected by the form of uncertainty surrounding their decisions. Following a Choquet-Brownian process to model ambiguity aversion on the dynamics of environmental damage, we study an international pollution control problem where countries may behave cooperatively or non-cooperatively. We show that carbon emissions decrease, as perceived ambiguity increases, in keeping with the precautionary principle, and such decrease is lower if countries behave non-cooperatively. We also examine the interrelation between the precautionary principle and the effects of a declining social discount rate and increase in population, and find that optimal policies induce more precaution. Our results have important implications for national strategies and actions to combat climate change.
License
This is an open access article distributed under the Creative Commons Attribution License which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Article Type: Research Article
EUR J SUSTAIN DEV RES, Volume 2, Issue 2, 2018, Article No: 21
https://doi.org/10.20897/ejosdr/85339
Publication date: 10 Mar 2018
Article Views: 5002
Article Downloads: 2970
Open Access HTML Content References How to cite this articleHTML Content
INTRODUCTION
The UN Sustainable Development Goals were agreed upon at the 70th session of the UN General Assembly in 2015, as part of the 2030 Agenda for Sustainable Development (UN, 2015), and since then progress has been made toward including them in the political debate worldwide. They encompass many sustainable development concepts, which have been formulated in seventeen specific goals, and among them, Goal number 13 prescribes countries to “take urgent actions to combat climate change and its impact” (UN, 2015). While it is now recognized that global warming is one of the biggest challenges of the planet, and (anthropogenic) emissions of a broad range of greenhouse gases (GHGs) of varying lifetimes and radiative forcing are major contributors, one important issue is “how to implement meaningfully and productively the UN SDGs to which so many countries have committed” (Rosen, 2017, page 2). In particular, it has been estimated that in order to stabilize global mean temperature increase at 2 degrees C - which is the limit temperature level computed by international climate scientists to avoid dangerous anthropogenic interference and adopted in the COP21 agreement -, the carbon budget of cumulative emissions should be approximately 0.8 Tt C (see Matthews et al, 2009), but large uncertainties in climate sensitivity prevent highly confident estimates of the emissions stabilization levels (see Pindyck, 2013; Heal and Millner, 2014). Traditional decision-making rules focus on calculable risk, so that outcomes and a subjective probability distribution over outcomes can be specified, and, under these circumstances, standard cost-benefit analyses and mitigation strategies aiming at reducing GHG emissions would be appropriate. However, in many cases, the possibility of irreversible and huge damages raises various questions about the nature of decision-making and what forms of uncertainty can be reasonably considered. GHGs with longer atmospheric residence (e.g., perfluorocarbons and sulfur hexafluoride), or climate damage profiles that include catastrophic events or other permanent consequences, together with unexpected environmental shocks, often determine a context of deep uncertainty. Here the distinction between risk and ambiguity comes into play. While “risk” refers to any sort of uncertainty that can be defined through the existence of a probabilistic model based on one single probability assessment, which is known to the decision-maker, “ambiguity” refers to situations in which the decision-maker appears to be not fully confident that his/her beliefs apply. Ambiguity applies to situations where uncertainty is incalculable, i.e. where there is no clear perception of the possible outcomes or of an estimate of a single plausible probability distribution (Gilboa, Postlewaite and Schmeidler, 2008).
The objective of this paper is to study in which way the strategies to combat climate change, as prescribed in the UN SDG number 13, are influenced by ambiguity aversion. Countries can tailor the UN SDGs to their priorities and situations, but the urgency in their planned actions to combat climate change and its impact is affected by the form of uncertainty surrounding their decisions. Several world-wide organizations called for a precautionary principle, to be applied by states under deep uncertainty conditions1. As Taleb et al (2014) write: ”the precautionary principle states that if an action or policy has a suspected risk of causing severe harm to the public domain (such as general health or the environment), and in the absence of scientific near-certainty about the safety of the action, the burden of proof about absence of harm falls on those proposing the action” (Taleb et al, 2014, p. 1).
We explore the implications of introducing ambiguity aversion in the evolution of natural systems and precautionary concerns from the point of view of policy actions in a stylized model with two countries. Our main reference in Section 2 is a standard set-up of the international pollution control model, firstly developed by Dockner and Van Long (1993), although here we introduce ambiguity. We adopt a Choquet-Brownian motion approach (see Section 3), which does not have to apply maxmin rules, as in the robust control approach (Hansen and Sargent, 2001), and therefore is not subject to the usual criticism that it is too conservative. Our main results in Section 3 show that carbon emissions should decrease, as perceived ambiguity increases, in keeping with the precautionary principle, and such decrease is lower if countries behave non-cooperatively. This result has important implication for national strategies and actions to combat climate change. We also examine the interrelation between the precautionary principle and the effects of a declining social discount rate, as found in recent literature (Section 5). As a further application of the precautionary principle, we show that if society is using effective discount rates that decline from a mean value of, say, around 4 percent per period for the immediate future down to around zero for the far-distant future, then, the choice of policy instruments and levels of desired stringency in terms of GHG targets should be based on more precaution. Furthermore, we study the impact of an increase in population on welfare (Section 6). It is well known that the rapid population growth will exacerbate all kinds of challenges, for food supplies, healthcare, social cohesion, poverty, pollution and global warming. Yet, the effects of an increase in population have not been assessed so far in an ambiguity framework. Our main result suggests that a fast growing population urges an even more cautious behaviour in the presence of deep uncertainty. Finally, concluding remarks are in Section 7.
THE MODEL
We consider a cooperative and a non-cooperative set-up of international pollution control with two countries, like in Dockner and Van Long (1993). Countries may act cooperatively (i.e. following a globally binding agreement) or non-cooperatively (i.e., there is no climate change protocol). Utility in each country is:
| \(U_{i}\)=\(a_{i}E_{i} - \frac{b_{i}}{2}E_{i}^{2}\), i=1,2 | (1) |
where \(E\) denotes emissions, \(a\) and \(b\) are positive coefficients. Utility is reduced by damages from global warming. The “damage function” is a notoriously weak link in the economics of climate change (Weitzman, 2010), and the welfare impacts seem to be highly dependent on the hypothesized functional form, especially at high temperatures. Following Weitzman (2010), a damage function that “does not excessively undermine reality” (Weitzman, 2010, page 61) and obeys a constant temperature-risk aversion coefficient property is
| \[D = \frac{\alpha T^{2}}{1 + \alpha T^{2}}\] | (2) |
where \(T\) stands for exogenously given global average surface temperature change above pre-warming level and \(\alpha\) is a positive coefficient. It is assumed that \(T\) can serve as an aggregate proxy for climate change. Provided that temperatures are not too high, that is, as \(\alpha T^{2}\) is small, expression (2) can be approximated as follows:
| \[D = \alpha T^{2}\] | (3) |
and, in view of Matthews et al. (2009), about the proportionality of global warming to cumulative carbon emissions, we can simplify it again as follows:
| \[D = \frac{\Omega_{i}}{2}P^{2}\] | (4) |
where \(P\) stands for the stock of global carbon pollutant and \(\Omega\) is a positive coefficient. Each country’s objective is to maximize welfare, that is:
| \[\text{ma}x_{E_{i}}\int_{0}^{\infty}e^{- \text{rit}}\left( a_{i}E_{i} - \frac{b_{i}}{2}E_{i}^{2} - \frac{\Omega_{i}}{2}P^{2} \right)\text{dt}\] | (5) |
subject to the damage dynamics, and \(r\) is the subjective rate used for discounting.
AMBIGUITY AND THE DAMAGE DYNAMICS
Let us suppose that each decision-maker (DM) is facing ambiguity on the damage dynamics. Uncertainty is introduced as a distorted stochastic process over the effects of the stock of carbon pollutant accumulating over time, where the distortion depends on the ambiguity of DM. We follow a capacity approach, where a capacity simultaneously represents the ambiguity experienced by the DM and his/her attitude towards this ambiguity (see also Chateauneuf, Eichberger and Grant, 2007; Agliardi, Agliardi and Spanjers, 2016). We refer to the combined effect of the perceived ambiguity and the DM’s ambiguity aversion as his/her ambiguity aversion bias. The capacity approach we adopt allows us to model the embedded ambiguity in a simple and parsimonious way, by representing the level of ignorance, hence the attitude towards ambiguity, throughout a single parameter, c. This makes it applicable to an empirical context.
More precisely, the damage dynamics is described employing a Choquet-Brownian process. A Choquet-Brownian process is a distorted Brownian process, where the distortion derives from the nature and intensity of preferences toward ambiguity (Kast, Lapied, 2010a, 2010b; Lapied and Toquebeuf, 2013). It is defined on the basis of a binomial lattice, where for each state \(s_{t}\) at time \(t\), \({s_{t + 1}}^{u}\) and \({s_{t + 1}}^{d}\) denote the possible successors at time \(t\)+1 for an “up” and a “down” movement, respectively. If “up” and “down” movements have the same capacity, then \(\upsilon({s_{t}}^{u}|s_{t})\ = \ \upsilon({s_{t}}^{d}|s_{t})\ = \ c\), where \(c\), \(0 < c < 1\), is a constant that represents the DM’s ambiguity about the likelihood of the states to come. It can be shown (Kast, Lapied, 2010a and Kast, Lapied and Roubaud, 2014) that such symmetric discrete process converges to a continuous time generalized Wiener process with mean equal to \(2c - 1\) and variance equal to \(4c(1 - c)\). A more general case, with asymmetric random walks, is studied in Agliardi (2017).
Here we assume that \(P_{t}\) follows a Choquet–Brownian process with this specification:
| \[\text{dP} = (E_{1} + E_{2} - \text{mP} + \nu_{i}\sigma)\text{dt} + s_{i}\sigma\text{dZ}\] | (6) |
where \(0 < m < 1\) is the environment’s self-cleaning capacity, \(\sigma\) is volatility, and \(Z\) is a Wiener process2. The continuous time generalized Wiener process in (6) has mean \(v_{i} = 2c_{i} - 1\) and variance \(s_{i}^{2} = 4c_{i}(1 - c_{i})\), where \(c_{i}\) denotes the capacity of country \(i\). Thus, the two parameters \(v_{i}\) and \(s_{i}^{2}\) assume different values depending on the degree of ambiguity aversion/propension of the country, or DM. If a country is ambiguity averse, the capacity is sub-linear, so that \(c < 1/2\) (Gilboa, Postlewaite and Schmeidler, 2008). If the perceived ambiguity increases, then the value of the parameter \(c\) moves further away from the anchor 1/2. Thus, the capacity becomes more convex (for an ambiguity averse DM) or more concave (for an ambiguity loving DM). The absence of an ambiguity bias is obtained as a special case for \(c = 1/2\). Notice that for ambiguity averse DMs we have \(- 1 < v < 0\) and \(0 < s < 1\), so that both drift and volatility are reduced in comparison to the case where ambiguity is absent.
THE BENCHMARK: COOPERATIVE VS NON-COOPERATIVE SOLUTIONS
The cooperative solution is obtained by maximizing expected joint welfare, defined by:
| \[W = \text{ma}x_{E_{i}}E\int_{0}^{\infty}{\sum_{i = 1}^{2}}e^{- r_{i}t}\left( a_{i}E_{i} - \frac{b_{i}}{2}E_{i}^{2} - \frac{\Omega_{i}}{2}P^{2} \right)\text{dt}\] | (7) |
where the dynamics of damage follows (6). For simplicity, let us focus on the case of two symmetric countries, so that we can drop sub-indexes \(i\). Optimality yields:
\[E^{*} = \frac{a + W_{P}^{'}}{b}\]
and the evolution of the GHGs stock can be obtained by the solution of the following stochastic differential equation:
\[\text{dP} = \left( \sum_{i}^{}\frac{a + W_{P}^{'}}{b} - \text{mP} + \nu\sigma \right)\text{dt} + s\sigma\text{dZ}\]
where the value function is of the form \(W = \frac{1}{2}\alpha P^{2} - \beta P - \gamma\). The expected value \(E(P)\) and its variance \(\text{Var}(P)\), corresponding to the cooperative solution, are:
| \[E(P) = P_{0}e^{- \rho t} + \mu\left( 1 - e^{- \rho t} \right)\] | (8) |
| \[Var(P) = \frac{s^{2}\sigma^{2}}{2\rho}(1 - e^{- 2\rho t})\] | (9) |
with \(\rho = 2\alpha + m,\ \mu = \frac{(r + m)(2a + \nu\sigma)}{(2\alpha + m)(r + 2\alpha + m)}\) and \(\alpha = \left( - \left( 2m + r \right) \pm \sqrt{(2m + r)^{2} + 16\Omega} \right)/4\), where \(b = 1\). Thus, the long-run (steady state level of) GHGs stock equals \(\mu\) and its variance \(\frac{s^{2}\sigma^{2}}{2\rho}\).
It can be verified that that the value function W decreases as perceived ambiguity aversion increases (the parameter \(c\) moves further away from the anchor ½). Moreover, both the expected value (8) and the variance (9) decrease, as perceived ambiguity aversion increases.
It implies that carbon emissions decrease, as perceived ambiguity increases, in keeping with the precautionary principle (see Taleb et al., 2014). Thus, if the countries have high concern about ambiguity, then they will adopt a more restrained policy, reducing emissions. The aim of the precautionary principle is to prevent DMs from running into the unexpected side effects of a certain type of decision (see also Athanassoglou and Xepapadeas, 2012).
Similarly, we can compute the non-cooperative solution, by maximizing each country’s welfare, subject to (6). Optimality yields:
\[E_{i}^{*} = \frac{a_{i} + {W_{i}}_{P}^{'}}{b_{i}}\]
and the evolution of the GHGs stock can be obtained by the solution of the following stochastic differential equation, as perceived by country \(i\):
\[\text{dP} = \left( \sum_{i = 1}^{2}\frac{a_{i} + {W_{i}}_{P}^{'}}{b_{i}} - \text{mP} + \nu_{i}\sigma \right)\text{dt} + s_{i}\sigma\text{dZ}\]
where the value function is of the form \(W = \frac{1}{2}\alpha_{i}P^{2} - \beta_{i}P - \gamma_{i}\).The expected value and variance corresponding to the non-cooperative solution are:
| \[E(P) = P_{0}e^{- \rho t} + \mu_{i}(1 - e^{- \rho t})\] | (10) |
| \[Var(P) = \frac{s^{2}{\sigma_{i}}^{2}}{2\rho}(1 - e^{- 2\rho t})\] | (11) |
with \(\rho = \sum_{i = 1}^{2}\frac{\alpha_{i}}{b_{i}} + m\), \(\mu_{i} = \frac{\sum_{i = 1}^{2}{\frac{a - \beta_{i}}{b_{i}} + \nu_{i}\sigma_{i}}}{\sum_{i = 1}^{2}{\frac{\alpha_{i}}{b_{i}} + m}}\).
Also in this case it can be verified that that the value functions \(W_{i}\) decrease as perceived ambiguity aversion increases (the parameter \(c_{i}\) moves further away from the anchor ½). Moreover, both the expected value (10) and the variance (11) decrease, as perceived ambiguity aversion increases. It implies that carbon emissions decrease, as perceived ambiguity increases, in keeping with the precautionary principle, although such decrease is lower than under the cooperative solution, i.e. there is less precaution if countries behave non-cooperatively. So there will be less precaution if countries do not cooperate, i.e. a standard free-rider problem. From expressions (10) and (11) we can actually show that the country which is more ambiguity averse (whose parameter \(c\) moves further away from the anchor ½) experiences more precaution, i.e. decreases carbon emissions at a larger extent. The greater the difference in perceived ambiguity between the two countries, the greater will be the difference in emissions.
Such results confirm most results in Xepapadeas (2011), although his model is built on a different ambiguity framework, which employs robust control methods and not a capacity approach.
DISCOUNTING THE DISTANT FUTURE: IMPLICATIONS OF DECLINING RATES
The appropriate “discount rate” to be used to evaluate environmental projects and activities has been long discussed in cost-benefit analyses and in climate change policies (see, f.e., Arrow et al. 1996). It is well known that the evaluation of environmental projects and their effects over hundreds of years are extremely sensitive to the discount rate. At the same time, positive discount rates lead us to place little weight on events in the distant future, such as effects arising from global warming. Arrow et al. (1996) describe normative arguments in favour of lower future discount rates. They argue that individuals tend to use a declining discount rate in the future, and this is more evident when valuations relate to an individual’s own lifetime versus future generations. In practice, they suggest policy-makers to apply lower discount rates to long-term, intergenerational projects. Weitzman (2001) proposes a theoretical approach to incorporate uncertainty about what discount rate to use in cost-benefit analysis. He demonstrates that even if every individual believes in a constant discount rate, the lack of consensus about what actual rate of interest should be used makes the effective social discount rate decline significantly over time. Following a different approach, also Newell and Pizer (2003) show that when the future path of the discount rate is uncertain and persistent, the distant future should be discounted at lower rates than the current rate.
The empirical counterpart of such studies is in Weitzman (2001), who first conducted a survey of more than 2000 economists asking them to state their “professionally considered gut feelings” on the appropriate real discount rate for valuing environmental projects to mitigate the effects of global climate change. They recommended a downward-sloping time profile of the discount rate schedule, with the following marginal discount rates (percent): 4 for immediate future (within years 1 to 5), 3 for near future (within years 6 to 25), 2 for medium future (within years 26 to 75), 1 for distant future (within years 76 to 300) and 0 for far-distant future (within years more than 300), yielding the equivalent “as-if-constant” discount rate equal to 1.75 percent per annum, much lower than the average discount rate of 4 percent.
In order to take into account the above-mentioned issue of the appropriate discount rate, let us modify the set-up and specify the objective function as follows:
\[\text{ma}x_{E_{i}}\int_{0}^{\infty}e^{- \int_{0}^{t}{r_{i}\left( \tau \right)d\tau}}\left( a_{i}E_{i} - \frac{b_{i}}{2}E_{i}^{2} - \frac{\Omega_{i}}{2}P^{2} \right)\text{dt}\]
where the downward-sloping time profile of the discount rate takes the shape of the step-function described above. In practice, it requires us to employ a discount rate equal to 1.75 percent.
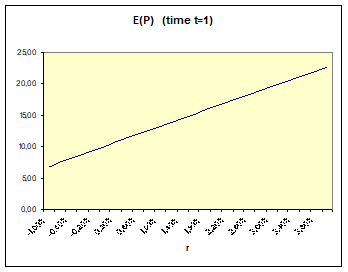
The relation between the expected value E(P) and the discount rate \(r\) is depicted in Figure 1. Similarly, also \(\text{Var}(P)\) is increasing in the discount rate \(r\). Thus, with a lower discount rate than the average rate both the expected value \(E(P)\) and the variance decrease. The implication is that if the countries base their analyses on lower discount rates, then they will adopt a more restrained policy, reducing carbon emissions and recommending more aggressive action to mitigate climate damage.
If society is using effective discount rates that decline from a mean value of, say, around 4 percent per period for the immediate future down to around zero for the far-distant future, then, the choice of policy instruments and levels of desired stringency in terms of GHG targets should be based on more precaution, because the consequences of climate damage would be more heavily concentrated in the future. This is another application of the precautionary principle.
DAMAGE AND THE INCREASE IN POPULATION
It is well known that the rapid population growth will exacerbate all kinds of challenges, for food supplies, healthcare, social cohesion, poverty, pollution and global warming. The world population projections estimate a 70% chance that the number of people on the planet will rise continuously from 7bn today to 11bn by 21003. Therefore, it is no surprise that there is now a strong argument that population should be on top of the international agenda.
In order to take into account the population growth, let us modify the set-up and specify the damage function as a function of the carbon pollutant \(P\) and population \(N\). For simplicity, let us assume that damage depends on \(P\) and \(N\) linearly:
| \[D = \frac{\Omega}{2}\text{PN}\] | (13) |
where the change in population is described by:
| \[\text{dN} = \text{nNdt}\] | (14) |
that is, \(n\) is the population growth rate, and carbon pollution follows expression (6) as before. Now, each country maximizes welfare, which can be specified as follows, supposing that the two countries are symmetric:
\[\text{ma}x_{E_{i}}\int_{0}^{\infty}e^{- \text{rt}}\left( aE_{i} - \frac{b}{2}E_{i}^{2} - \frac{\Omega}{2}\text{PN} \right)\text{dt}\]
If the two countries act cooperatively, then we can formulate the optimal control problem and the corresponding Hamilton-Jacobi-Bellman equation becomes:
\[rW = \text{ma}x_{E_{i}}\left( \sum_{i = 1}^{2}a_{i}E_{i} - \frac{b_{i}}{2}E_{i}^{2} - \Omega\text{PN} \right) + W_{P}^{'}dP + W_{N}^{'}dN + \frac{s^{2}\sigma^{2}}{2}W_{\text{PP}}^{''}\]
where the value function is:
| \[W = \alpha P^{2} + \beta N^{2} + \text{γPN} + \text{δP} + \text{εN} + \vartheta\] | (15) |
\(W_{P}^{'}\), \(W_{N}^{'}\) and \(W_{\text{PP}}^{''}\) denote the first and second derivatives of the value function. Optimality implies:
\[E^{*} = a + 2\text{αP} + \text{γN} + \delta\]
and two solutions are obtained, that is, either:
\[\alpha = \frac{r + 2m}{4}\]
\[\beta = \frac{- \Omega^{2}}{(2n - r)(n + m)^{2}}\]
\[\gamma = \frac{\Omega}{n + m}\]
\[\delta = - \frac{(r + 2m)(2a + \nu\sigma)}{2m}\]
\[\varepsilon = \frac{\Omega(2a + \nu\sigma)}{(r - n)(n + m)}\]
\[\vartheta = \left( 4m^{2}a^{2} + r\left( 2a + \text{νσ} \right)^{2} + s^{2}\sigma^{2}\left( r + 2m \right)m^{2} \right)/4rm^{2},\]
or:
\[\alpha = 0,\beta = \frac{- \Omega^{2}}{(2n - r)(n - m - r)^{2}},\ \gamma = \frac{\Omega}{n - m - r},\ \delta = 0,\ \varepsilon = \frac{\Omega(2a + \text{νσ})}{(r - n)(n - m - r)},\ \vartheta = a^{2}/\text{r.}\]
Observe that \(\alpha,\beta,\gamma\) do not change as the parameter \(c\) changes, that is, are not affected by ambiguity, while \(\delta,\varepsilon\) and \(\vartheta\) change, as perceived ambiguity increases (i.e., the parameter \(c\) moves further away from the anchor ½). Numerical simulations show that the welfare function decreases as perceived ambiguity increases. Moreover, we can compute the expected value \(E(P)\) and the variance \(\text{Var}(P)\), that is:
| \[E(P) = P_{0}e^{- \text{ρt}} + \mu\left( 1 - e^{- \text{ρt}} \right)\] | (16) |
| \[Var(P) = \frac{s^{2}\sigma^{2}}{2\rho}\left( 1 - e^{- 2\text{ρt}} \right)\] | (17) |
where \(\rho = - (4\alpha - m)\) and \(\mu = \left( 2\left( a + N\gamma + \delta \right) + \nu\sigma \right)/\left( - \left( 4\alpha - m \right) \right)\).
Optimal carbon emissions increase with \(P\) and \(N\). Let us study how the value function (15) changes with population and pollution.
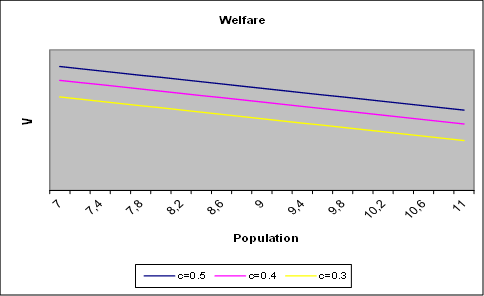
Numerical simulations show that the value function decreases as population increases. Figure 2 shows an example, where most parameters are taken from Xepapadeas (2011), that is \(P = 590\) GtC, \(a = \ 224\$/\text{tC}\), \(\Omega = 0.0223 \times 10^{9}\$/\left( \text{GtC} \right)^{2}\), \(m = 0.0083\), \(r = 0.03\), \(\sigma = 0.2343\ GtC\).
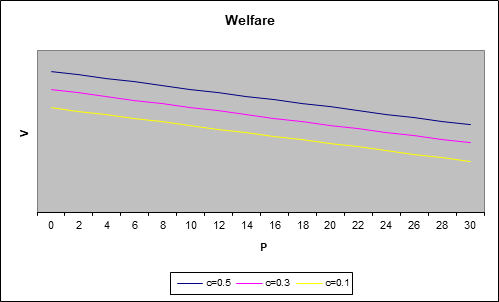
Numerical simulations show that the value function decreases as the stock of pollutant increases.
Figures 2 and 3 show how welfare is decreased as perceived ambiguity increases.
Again, we find that as perceived ambiguity increases, in order to avoid potentially severe damages, the policy maker adopts a precautionary policy. Precaution is costly, and this cost is measured by the reduction in the value function as perceived ambiguity increases.
These results confirm on one side the robustness of the precautionary principle, which still holds for an alternative damage function, and, on the other side, suggest that a fast-growing population urges an even more cautious behaviour in the presence of deep uncertainty.
CONCLUDING REMARKS
There are various extensions that can be studied employing the above framework. One refers to the interplay between mitigation and adaptation strategies. It is often claimed that mitigation of GHGs and adaptation to climate change are complementary strategies to deal with climate change, meaning that both are useful to reduce the climate change damages. Mitigation addresses the source of the climate change problem by reducing the amount of emitted GHGs. It typically deals with a global public good. Adaptation, on the contrary, provides purely local benefits, usually limited to the period in which adaptation takes place. Both effects of mitigation and adaptation have not been studied in the above framework so far.
Another crucial variable which has never been endogenized is population. It is well known that the rapid population growth will exacerbate all kinds of challenges, for food supplies, healthcare, social cohesion, poverty, pollution and global warming. This issue has to be seriously taken into account in designing the strategies to achieve the UN SDGs in particular and, more generally, towards sustainable development globally.
-
For example, the Rio Declaration on Environment and Development states: “In order to protect the environment, the precautionary approach shall be widely applied by states according to their capabilities. Where there are threats of serious or irreversible damage, lack of full scientific certainty shall not be used as a reason for postponing cost-effective measures to prevent environmental degradation”.↩
-
Expression (6) is obtained from \(\text{dP} = (E_{1} + E_{2} - \text{mP})\text{dt} + \sigma\text{dW}\), where \(W_{t} = v_{i}t + s_{i}^{\ }\ Z\) and \(W\) is a Wiener process.↩
-
Sub-saharan Africa is set to be by far the fastest growing region, with population rocketing from 1bn today to between 3.5 and 5bn in 2100. Nigeria, the continent’s most populous nation, is expected to an increase in population from 200m today to 900m by 2100 (Science, 10 Oct. 2014).↩
References
- Agliardi, E (2011) Sustainability in Uncertain Economies. Environmental and Resource Economics, 48, 71-82. https://doi.org/10.1007/s10640-010-9398-x
- Agliardi, E., Agliardi R. and W. Spanjers (2016). Corporate Financing Decisions under Ambiguity: Pecking Order and Liquidity Policy Implications. Journal of Business Research, 69, 6012-6020. https://doi.org/10.1016/j.jbusres.2016.05.016
- Agliardi, R. (2017) Asymmetric Choquet random walks and ambiguity aversion or seeking. Theory and Decisions, 83, 591–602. https://doi.org/10.1007/s11238-017-9632-x
- Arrow, K. J., Cline, W. R., Maler K-G., Munasinghe, M., Squitieri, R. and Stiglitz, J. E. (1996). Intertemporal equity, discounting and economic efficiency. In j.P. Bruce, H. Lee, E.F. Haites (eds) Climate change 1995-Economic and social dimensions of climate change, Cambridge University Press, Cambridge UK.
- Athanassoglou, S. and Xepapadeas, A. (2012). Pollution control with uncertain stock dynamics: when, and how, to be precautious. Journal of Environmental Economics and Management, 63, 304-320. https://doi.org/10.1016/j.jeem.2011.11.001
- Chateauneuf, A., Eichberger, J. and Grant, S. (2007). Choice under capacities with the best and the worst in mind: Neo-Additive capacities. Journal of Economic Theory, 137, 538–567. https://doi.org/10.1016/j.jet.2007.01.017
- Dockner, Engelbert J. and Long, N. V. (1993). International Pollution Control: Cooperative versus Noncooperative Strategies. Journal of Environmental Economics and Management, 25(1), 13–29. https://doi.org/10.1006/jeem.1993.1023
- Gilboa, I., Postlewaite, A. and Schmeidler, D. (2008). Probability and Uncertainty in Economic Modelling. Journal of Economic Perspectives, 22, 173–188. https://doi.org/10.1257/jep.22.3.173
- Gollier, C., Jullien, B. and Triech, N. (2000). Scientific progress and irreversibility: an economic interpretation of the Precautionary principle. Journal of Public Economics, 75, 229-253. https://doi.org/10.1016/S0047-2727(99)00052-3
- Hansen, L. P and Sargent, T. J. (2001). Robust control and model uncertainty. American Economic Review, 91, 60-66. https://doi.org/10.1257/aer.91.2.60
- Heal, G. and Millner, A. (2014). Uncertainty and decision making in climate change economics. Rev Environ Econ Policy, 8(1), 120–137. https://doi.org/10.1093/reep/ret023
- Kast, R. and Lapied, A. (2010a). Valuing future cash flows with non separable discount factors and non additive subject measures: conditional Choquet capacities on time and uncertainty. Theory and Decision, 69(1), 27-53. https://doi.org/10.1007/s11238-008-9107-1
- Kast, R. and Lapied, A. (2010b). Dynamically consistent Choquet random walk and real investments. Document de Travail n. 2010-33, GREQAM, HAL id: halhs-00533826
- Kast, R., Lapied, A. and Roubaud, D. (2014). Modelling under ambiguity with dynamically consistent Choquet random walks and Choquet-Brownian motions. Economic Modelling, 495-503. https://doi.org/10.1016/j.econmod.2014.01.007
- Kelsey, D. and Spanjers, W. (2004). Ambiguity in partnership. The Economic Journal, 114, 528-546. https://doi.org/10.1111/j.1468-0297.2004.00230.x
- Lapied, A. and Toquebeuf, P. (2013). A note on "Re-examining the law of iterated expectations for Choquet decision makers". Theory and Decision, 74, 439-445. https://doi.org/10.1007/s11238-012-9297-4
- Matthews, H. D., Gillett, N. P., Stott, P. A. and Zickfield, K. (2009). The proportionality of global warming to cumulative carbon emissions. Nature, 459, 829-833. https://doi.org/10.1038/nature08047
- Newell, R. G. and Pizer, W. A. (2003) Discounting the distant future: how much do uncertain rates increase valuation? Journal of Environmental Economics and Management, 46, 52-71. https://doi.org/10.1016/S0095-0696(02)00031-1
- Rosen, M. A. (2017). How can we achieve the UN Sustainable Development Goals? European Journal of Sustainable Development Research, 1(2), 6. https://doi.org/10.20897/ejosdr.201706
- Taleb, N. N., Read, R., Douady, R., Norman, J., Bar-Yam Y. (2014). The Precautionary Principle (with applications to the genetic modification of organisms). Extreme Risk Initiative. NYU School of Engineering Working Paper Series, 1-24.
- UN 2015. Resolution of the General Assembly on 25 Sept. 2015. A/RES/70/1. 70th Session, United Nations
- Weitzman, M. L. (2001). Gamma discounting. American Economic Review, 91, 260-271. https://doi.org/10.1257/aer.91.1.260
- Weitzman, M. L. (2010). What is the “damages function” for global warming – and what difference might it make? Journal of Climate Change Economics, 1, 57-69. https://doi.org/10.1142/S2010007810000042
- Xepapadeas, A (2011). The cost of ambiguity and robustness in international pollution control. Climate Change and Common sense. Essays in Honour of Tom Schelling.
How to cite this article
APA
Agliardi, E. (2018). How Can We “Take Urgent Action to Combat Climate Change and its Impact” (UN SDG N.13) under Ambiguity Aversion?. European Journal of Sustainable Development Research, 2(2), 21. https://doi.org/10.20897/ejosdr/85339
Vancouver
Agliardi E. How Can We “Take Urgent Action to Combat Climate Change and its Impact” (UN SDG N.13) under Ambiguity Aversion?. EUR J SUSTAIN DEV RES. 2018;2(2):21. https://doi.org/10.20897/ejosdr/85339
AMA
Agliardi E. How Can We “Take Urgent Action to Combat Climate Change and its Impact” (UN SDG N.13) under Ambiguity Aversion?. EUR J SUSTAIN DEV RES. 2018;2(2), 21. https://doi.org/10.20897/ejosdr/85339
Chicago
Agliardi, Elettra. "How Can We “Take Urgent Action to Combat Climate Change and its Impact” (UN SDG N.13) under Ambiguity Aversion?". European Journal of Sustainable Development Research 2018 2 no. 2 (2018): 21. https://doi.org/10.20897/ejosdr/85339
Harvard
Agliardi, E. (2018). How Can We “Take Urgent Action to Combat Climate Change and its Impact” (UN SDG N.13) under Ambiguity Aversion?. European Journal of Sustainable Development Research, 2(2), 21. https://doi.org/10.20897/ejosdr/85339
MLA
Agliardi, Elettra "How Can We “Take Urgent Action to Combat Climate Change and its Impact” (UN SDG N.13) under Ambiguity Aversion?". European Journal of Sustainable Development Research, vol. 2, no. 2, 2018, 21. https://doi.org/10.20897/ejosdr/85339

 Full Text (PDF)
Full Text (PDF)