Abstract
The performance of steam power plants, utilizing recovered waste heat from air-fuel and oxy-fuel combustion, are compared. Temperature profiles in the heat recovery steam generator (HRSG), steam production rate, net-work output and energy efficiency are simulated for different conditions. Investigations are made into the effect of varying pinch point on HRSG performance, net-work and energy efficiency for power generation utilizing oxy-fuel combustion. It is found that with increased pinch point there is an associated decrease in HRSG and steam plant efficiencies. Exhaust gas composition influences the energy efficiency of the power plant. When air-fuel and oxy-fuel combustion are compared there is a reduced amount of nitrogen in the oxidant stream in the latter case. When comparing air-fuel and oxy-fuel combustion, a considerable deviation in HRSG and steam power plant performance is exhibited, with oxy-fuel combustion offering benefits in system efficiency and plant output. The exhaust gas composition at the HRSG inlet contributes significantly the performance characteristics of the system. Raising the HRSG inlet temperature also increases power generation and system efficiency. The results provide insights into the use of oxy-fuel combustion for systems utilizing HRSG for power generation while demonstrating the influence of gas composition, pinch point, and exhaust gas temperature on system performance, and suggest that oxy-fuel combustion can help enhance the contribution to sustainable development of some energy systems.
License
This is an open access article distributed under the Creative Commons Attribution License which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Article Type: Research Article
EUR J SUSTAIN DEV RES, Volume 2, Issue 2, 2018, Article No: 22
https://doi.org/10.20897/ejosdr/69787
Publication date: 11 Mar 2018
Article Views: 5378
Article Downloads: 3277
Open Access HTML Content References How to cite this articleHTML Content
INTRODUCTION
In recent years growing energy demand and greenhouse gas emissions has led to the development of advanced energy systems with increased efficiency, reduced environmental impact and enhanced sustainability. Waste heat recovery, renewable energy utilization, cogeneration, combined cycle power generation and energy storage have all attracted much interest (Liang et al., 2013; Kuravi et al., 2013; Uchida et al., 2013; El-Khattam and Salama, 2004; Nag and De; 1997). Waste heat is available from many industries and can be used for power generation using a heat recovery steam generator (HRSG) (Feng et al., 2014; Karellas et al., 2013).
Many studies have been conducted on various applications for waste heat recovery using HRSGs. For example, Karellas et al. (2013) investigate the use of an HRSG to collect waste heat from cement processes. Also, Shu et al. (2013) investigate the use of HRSGs with two stroke motors, Carazas et al. (2011) examine the use of HRSGs in several power generating plants, Beér (2013) investigates the use of HRSGs in CO2 reduction in coal power generating plants, and Karthikeyan et al. (1998) analyzed steam production rates and net-work for a cogeneration system using industrial waste heat recovery.
Numerous HRSG applications exist. One common application is in combined cycles, where waste heat is transferred from gas turbine exhaust gases, to water for producing steam for power production in a Rankine cycle (Wang et al., 2011; Ong’iro et al., 1997). It has been found that combined cycles can enhance the efficiency, economics and environmental aspects of power production using gas turbine cycles (de Gouw et al., 2014; Ganjehkaviri et al., 2014; Valdes et al., 2004). HRSG characteristics have been shown to affect significantly the technical and economic operation of combined cycles (Rovira et al., 2011; Rahim, 2012; Ganapathy, 1996). Studies have been conducted on the design and optimization of HRSGs under varying operating conditions to improve understanding of the most significant characteristics (Franco and Russo, 2002; Ghazi et al., 2012; Mansouri et al., 2012; Leduc et al., 2011; Cenusa et al., 2004; Butcher and Reddy, 2007).
Air is a common oxidant and is used in the majority of combustion processes. Combustion can be improved by using an oxidant that has an increased proportion of oxygen than found in atmospheric air. Pure oxygen can be utilized as the oxidant; the process is known as oxy-fuel combustion (Toftegaard et al., 2010; Wall et al., 2009). Oxy-fuel combustion offer advantages including reduced CO2 emissions from combustion, reduced requirements for emission control and other equipment, and increased potential for carbon capture (Toftegaard et al., 2010; Wall et al., 2009; Nord et al., 2009). Much research has been reported on oxy-fuel combustion of coal for power production (Wall et al., 2009; Wall et al., 2011; Chen et al., 2012; Yoshiie et al., 2014). Oxy-fuel combustion of natural gas has been explored to a lesser extent but studies show that it is beneficial in natural gas power plants (Nord et al., 2009). Oxy-fuel combustion of natural gas has also shown potential for increased output response rates, decreased fuel consumption, decreased emissions and enhanced sustainability in a gas power plant settings (Nord et al., 2009; Wu et al., 2010).
Despite the insights gained through past research, reports are sparse on the effect of oxy-fuel combustion, in combined cycles, on HRSG and Rankine cycle performance. Little is known about the influence of exhaust gas temperature, pinch point and other operating parameters on energy efficiency when oxy-fuel combustion is employed. The objective of this research is to determine whether the utilization of oxy-fuel combustion, in a combined cycle, has a significant effect on the HRSG and Rankine cycle performance. This study investigates the effects of using oxy-fuel combustion on the performance of both a HRSG and Rankine cycle using energy analysis. To improve the understanding of HRSG and Rankine cycle performance characteristics while using oxy-fuel combustion parametric studies are also conducted to investigate the influence of pinch point and HRSG gas inlet temperature. The results are compared to air-fuel combustion to illustrate possible benefits and drawbacks to utilizing oxy-fuel combustion on HRSG and Rankine cycle performance within a combined cycle arrangement, in terms of various factors including potential contribution to sustainable development.
SYSTEM DESCRIPTION
In this study, a single pressure HRSG that includes an economizer, evaporator and superheater is considered. The HRSG provides energy for steam production within a steam power plant (see Figure 1).
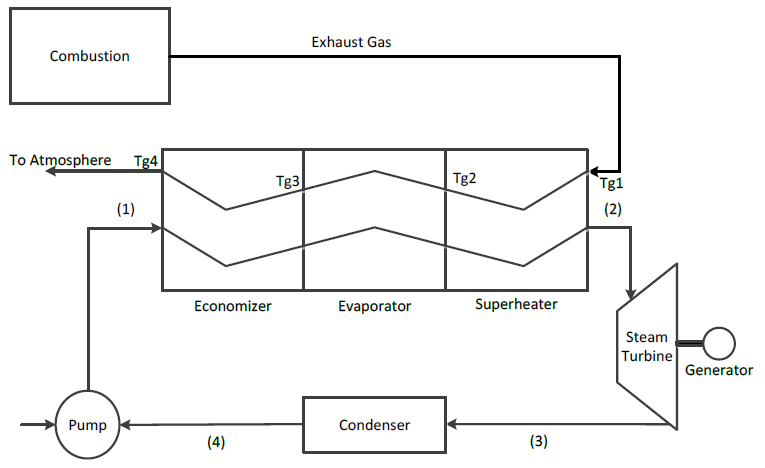
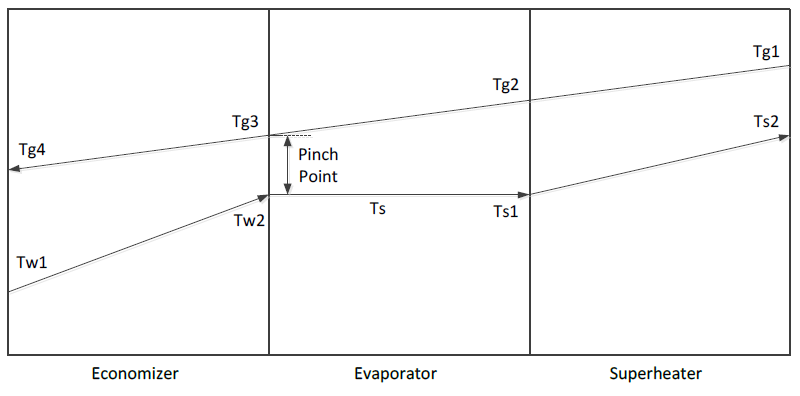
Figure 2 illustrates the temperature profile in the HRSG. Hot exhaust gas from combustion enters the superheater and flows through the evaporator and economizer and is discharged at the exit of the economizer to the surroundings. Water enters the economizer at temperature and is heated to saturation before entering the evaporator to create a saturated steam. The saturated steam at enters the superheater and exits as superheated steam, which is conveyed to the steam turbine.
The fuel is taken to be natural gas with the same composition as that used by Cihan et al. (2006). Typically natural gas fired powered plants utilize air-fuel combustion; a more recent idea is to use pure oxygen in combustion. Different exhaust gas compositions result for the two processes, as listed in Table 1.
|
Table 1. Exhaust gas composition for two methods fuel combustion in the electricity generation system
*Values taken from Cihan et al. (2006) |
|||||||||||||||||
The composition of the exhaust gas for oxy-fuel combustion is found through a balanced chemical equation using the natural gas composition given by Cihan et al. (2006) and pure oxygen as the oxidant with the same amount of excess oxygen as used in air-fuel combustion to maintain the amount of fuel in each scenario. It is common for oxy-fuel systems to replace the missing nitrogen through recirculating CO2, since producing pure oxygen is typically energy consuming and expensive. For this study it is assumed that nitrogen is not replaced; this allows for a comparison of HRSG and power plant performance when CO2 recirculation is not employed. The amount of excess oxygen is determined by comparing of the amount of oxygen utilized in the actual chemical reaction to the theoretical chemical equation where no excess oxygen is utilized. Balanced chemical equations are developed based on the work of Cihan et al. (2006) under the assumption that all components are ideal gases. The balanced chemical equation for the air-fuel combustion reaction is
| \[\left( 0.98998\ CH_{4} + 0.00114\ C_{2}H_{6} + 0.00037\ C_{3}H_{3} + 0.00018\ C_{4}H_{10} + 0.0004\ C_{5}H_{12} + 0.00808\ N_{2} + 0.00021\ CO_{2} \right) + 7.12\ \left( O_{2} + 3.76\ N_{2} \right) \rightarrow 1.0028\ CO_{2} + 1.9033\ H_{2}O + 5.1658\ O_{2} + 26.771\ N_{2}\] | (1) |
Comparing the above chemical equation to that for combustion with no excess oxygen shows that the combustion reaction used by Cihan et al. (2006) was performed with 257% excess oxygen. The balanced chemical equation for oxy-fueled combustion with the same degree of excess oxygen is
| \[\left( 0.98998\ CH_{4} + 0.00114\ C_{2}H_{6} + 0.00037\ C_{3}H_{3} + 0.00018\ C_{4}H_{10} + 0.0004\ C_{5}H_{12} + 0.00808\ N_{2} + 0.00021\ CO_{2} \right) + 7.12\ O_{2} \rightarrow 1.0028\ CO_{2} + 1.9033\ H_{2}O + 5.1658\ O_{2} + 0.00808\ N_{2}\] | (2) |
ASSUMPTION
The assumed operating conditions for the HRSG and Rankine cycle are adapted from studies done by Butcher and Reddy (2007) and Cihan et al. (2006) and are listed in Table 2.
|
Table 2. Operating parameters for the electricity generation system
* Values coincide with those utilized in studies by Butcher and Reddy (2007) and Cihan et al. (2006) |
The following general assumptions are also made in this study:
-
System operates at steady state
-
Pressure drops throughout the steam cycle are negligible
-
Specific heats of exhaust gas are dependent on temperature
ANALYSIS
The exhaust gas temperature at the inlet of the economizer in the HRSG is:
| \[T_{g3} = \ T_{\text{sat}} + PP\] | (3) |
where \(T_{g3}\) is the gas temperature at the evaporator exit, \(T_{\text{sat}}\) is the saturation temperature of the water at the evaporator pressure and \(\text{PP}\) is the HRSG pinch point.
Applying an energy balance to the gas and steam streams in the evaporator and superheat sections, the steam production rate, \({\dot{m}}_{s}\), for the HRSG is found as follows:
| \[{\dot{m}}_{s} = \frac{{\dot{m}}_{g}\left( c_{pTg1}T_{g1} - c_{pTg3}T_{g3} \right)(1 - hl)}{(h_{s2} - h_{w2})}\] | (4) |
where \(T_{g1}\) is the HRSG gas inlet temperature, \(T_{g3}\) is the gas temperature at the exit of the evaporator, \({\dot{m}}_{g}\) is the exhaust gas mass flow rate,\(\ c_{\text{pTgi}}\) is the specific heat of the gas at location \(T_{\text{gi}}\), \(\text{hl}\) is the heat loss from the exhaust gas within the HRSG, \(h_{s2}\) is the specific enthalpy of the steam at the superheater exit and \(h_{w2}\) is the specific enthalpy of water at the evaporator inlet (\(T_{w2}\)). Also, \(h_{s2}\) is determined using the assumed temperature and pressure conditions within the HRSG and \(h_{w2}\) using the saturated liquid conditions at the associated HRSG pressure.
The temperature of exhaust gas leaving the superheater is determined through an energy balance across it. An iterative process, where \(c_{pTg2}{= c}_{pTg1}\) is initially assumed, is applied to solve for \(T_{g2}\):
| \[T_{g2} = \frac{c_{pTg1}T_{g1}}{c_{pTg2}} - \frac{{\dot{m}}_{s}(h_{s2} - h_{s1})}{{\dot{m}}_{g}c_{pTg2}(1 - hl)}\] | (5) |
where \(h_{s1}\) is the enthalpy at the evaporator exit (\(T_{s1}\)). Using the calculated value for \(T_{g2}\) a new specific heat is used to repeat the calculation for \(T_{g2}\) using Eq. (5) to provide a more accurate estimation of gas temperature.
The exhaust gas temperature at the exit of the HRSG is found using an energy balance across the economizer:
| \[T_{g4} = \frac{c_{pTg3}T_{g3}}{c_{pTg4}} - \frac{{\dot{m}}_{s}(h_{w2} - h_{w1})}{{\dot{m}}_{g}c_{pTg4}(1 - hl)}\] | (6) |
where \(h_{w1}\) is the specific enthalpy of the water at the inlet of the economizer. Using the calculated value for \(T_{g4}\) a new specific heat is used to repeat the calculation for \(T_{g4}\) using Eq. (6) to provide a more accurate estimation of gas temperature.
The exhaust gas is assumed to be an ideal gas mixture and its specific heat is determined through the summation of the specific heats (\(c_{\text{pi}})\) of each component, \(i\), and their mass fraction \({(mf}_{i})\):
| \[c_{p}\left( T \right) = \sum_{i = 1}^{n}\text{mf}_{i}c_{\text{pi}}(T)\] | (7) |
The rate of net-work output from the steam cycle, \({\dot{W}}_{\text{net}}\), is the difference in the turbine shaft work output rate, \({\dot{W}}_{\text{turbine}}\), and the input work rate of the pumps, \({\dot{W}}_{\text{pump}}\):
| \[{\dot{W}}_{\text{net}} = \ {\dot{W}}_{\text{turbine}} - {\dot{W}}_{\text{pump}}\] | (8) |
The energy efficiency of the HRSG/steam cycle combination \(\eta_{\text{system}}\) is the ratio of the net-work output rate to the heat input rate, where the heat input rate is energy rate associated with the exhaust gas as it enters the HRSG. That is,
| \[\eta_{\text{system}} = \frac{{\dot{W}}_{\text{net}}}{{\dot{Q}}_{\text{input}}} = \frac{{\dot{W}}_{\text{net}}}{{{\dot{m}}_{g}c}_{pTg1}T_{g1}}\] | (9) |
where \({\dot{Q}}_{\text{input}}\) is the energy flow rate of the exhaust gas at the inlet of the HRSG which is a function of the specific heat, the mass flow rate and the temperature of the exhaust gas.
RESULTS AND DISCUSSION
Gas composition is varied, through assuming natural gas combustion using air and pure oxygen as oxidants. The pinch point influences the temperature profile and steam production rate in a HRSG when air- and oxy-fuel combustion is utilized. The effect of inlet temperature on energy efficiency is also explored. Results are compared for systems utilizing air and oxy-fuel combustion.
Investigation of HRSG Steam Production Rates and Temperature Profiles on Different Pinch Points in HRSGs Using Exhaust Gas from Air- and Oxy-fuel Combustion Processes
In this analysis, pinch point is varied and all other parameters in Table 2 are held constant. The effect of pinch point on the temperature profiles of the water/steam and exhaust gas sides in a HRSG are shown in Figures 3 and 4 for air-fuel and oxy-fuel combustion, respectively. Reducing the pinch points decreases gas temperatures entering the economizer, which indicates there is more energy extracted from the exhaust gas in the superheater and evaporator, which results in increased steam production rate. There is an increase in the heat transfer rate within the economizer and a reduction in exit gas temperatures with a decreasing pinch point, which is represented by a slight divergence in the exhaust gas temperatures for the different pinch points in the economizer. The divergence is caused by a variation in the exhaust gas specific heat given the temperatures associated with the set pinch point. For the pinch points investigated it is found that the specific heat of the exhaust gas mixtures increases with temperature, which results in a decrease in the temperature difference for the exhaust gas within the economizer.
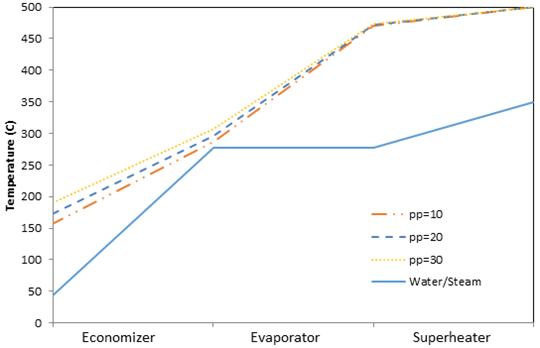
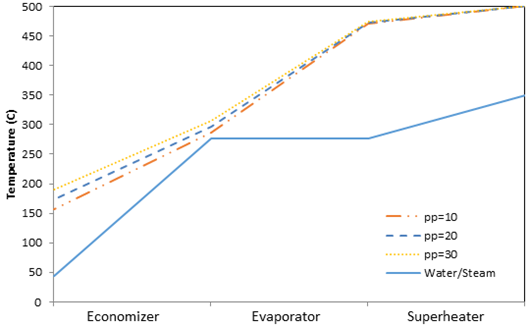
Low exhaust gas temperatures at the HRSG exit indicates a high degree of waste heat utilization in the HRSG and is associated with an increased steam production rate and system efficiency. The variation in steam production rate with pinch point is illustrated in Figure 5, for both air-fuel and oxy-fuel combustion. Lower pinch points increase the amount of steam that can be generated within the HRSG due to increased thermal energy transfer to the water/steam in the HRSG evaporator. When the pinch point is increased the exhaust gas temperature in the evaporator, in the economizer and at the exit of the HRSG are increased.
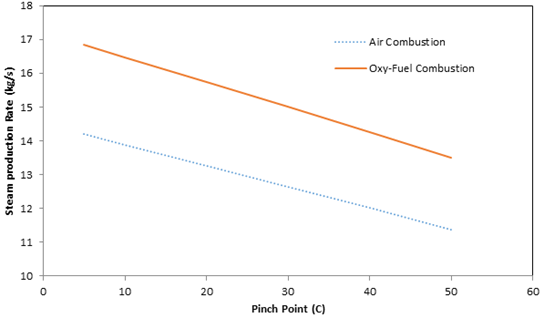
Air-fuel and oxy-fuel combustion are observed to exhibit similar trends regarding the relation between steam production rate to the pinch point; specifically, the steam production rate decreases with increasing pinch point. It is seen in Figure 5 that oxy-fuel combustion has a higher steam production rate then air-fuel combustion for the same pinch point. This trend is caused by a difference in the specific heat associated with the exhaust gases produced by air- and oxy-fuel combustion processes. For the values investigated, the specific heat of the exhaust gas for oxy-fuel combustion is higher than for air-fuel combustion; this observation correlates well with the results of Zheng et al. (2004), which demonstrate that increased CO2 content in exhaust gases raises the specific heat. As a result more thermal energy is transferred from the exhaust gas for the production of steam. Figure 5 also illustrates that the trends for air-fuel combustion and oxy-fuel combustion are not parallel. Due to a difference in exhaust gas composition for the two combustion processes, the specific heat values change nonlinearly relative to one another. For example at 150°C the specific heats of the combustion gases for air-fuel and oxy-fuel combustion are 105.7 kJ/kg·K and 109.7 kJ/kg·K respectively, a difference of 3.1%. At 500°C the specific heats for air-fuel and oxy-fuel combustion are 114.1 kJ/kg·K and 122.8 kJ/kg·K respectively, a difference of 7%.
Effect of Inlet Temperature and Oxy-fuel Combustion on Energy Efficiency of Waste Heat Recovery Power Generation System
In this analysis, all parameters in Table 2 are held constant while the HRSG gas inlet temperature is varied. The effect of HRSG gas inlet temperature on steam production rate is illustrated in Figure 6. The steam production rate increases with HRSG inlet temperature for both air- and oxy-fuel combustion, indicating that more energy is transferred to the steam side of the HRSG when gases are cooled from a higher temperature to the evaporator exit temperature set by the pinch point. Butcher and Reddy (2007) found similar results with increasing steam production with increasing exhaust gas inlet temperatures.
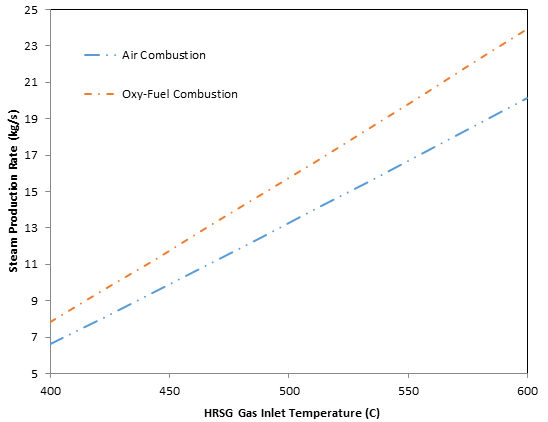
The steam production rate associated with oxy-fuel combustion is higher than that with air-fuel combustion over the range of exhaust inlet temperatures considered. The amount of energy transferred to the water/steam side from the oxy-fuel exhaust gas is higher than the energy transferred by the air-fuel combustion gases. This is due to the specific heat of the oxy-fuel gases being higher than that of the air-fuel gases. From Eq. (5), the only difference between the cases is the specific heat of the exhaust gases. Even though this study utilizes variable specific heats, the specific heat for the oxy-fuel gases remains higher than for the air-fuel gases throughout the HRSG for all temperatures investigated.
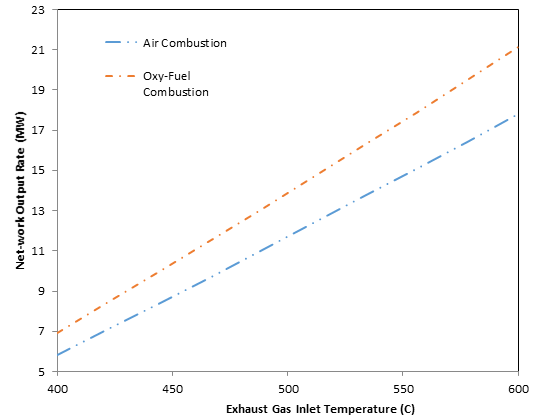
The variation in net-work output with HRSG gas inlet temperature is shown in Figure 7. Overall the net-work output increases with higher HRSG gas inlet temperatures due to the increased steam production rate in the HRSG. Overall the system arrangement utilizing oxy-fuel combustion has a higher net-work output compared to air-fuel combustion. This is expected because of the increased steam production rate with oxy-fuel production, due to differences in composition and specific heat.
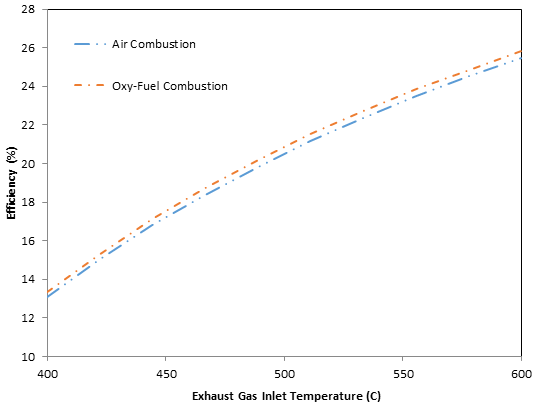
The results show that the use of oxy-fuel combustion enhances the HRSG and steam cycle system performance. The effect of using oxy-fuel combustion on energy efficiency is shown in Figure 8. Overall, oxy-fuel combustion increases the system efficiency and the increase becomes more pronounced at higher temperatures. The trends are a result of varying specific heat and the amount of thermal energy available at the inlet of the HRSG. This observation agrees with the findings of Butcher and Reddy (2007) and Carcasci and Facchini (2000).
CONCLUSIONS
It is found that the use of oxy-fuel combustion influences HRSG and system efficiency. The energy efficiency of the steam power plant, in combined cycles, increases with gas inlet temperature when pinch point and steam production conditions are held constant.
The HRSG and steam power plant energy efficiencies decrease with increased pinch point. Overall, pinch point is a significant parameter that determines steam production rate and system performance.
HRSG and steam power plant efficiency are highly influenced by the HRSG gas inlet temperature. When pinch point is held constant, increasing the HRSG gas inlet temperature increases the degree of waste heat recovery through transferring more energy for steam production. Oxy-fuel combustion offers an increase in system efficiency over air-fuel combustion and the increase in efficiency is more prominent at higher HRSG gas inlet temperatures.
Using oxy-fuel combustion positively influences HRSG efficiency. Increased energy transfer from the oxy-fuel exhaust gas through the HRSG allows for increased net-work output compared to a system using air-fuel combustion. This result is mainly attributable to the higher specific heat associated with the oxy-fuel combustion exhaust gas.
The use of oxy-fuel combustion is shown to be beneficial to HRSG and steam power plant performance in a combined cycle arrangement, and can contribute to sustainable development. Oxy-fuel may also beneficial for other components and processes in a complete combined cycle, such as combustion in the combustion chamber and expansion in the gas turbine. Further investigations should be conducted into the benefits of oxy-fuel combustion on a complete system. Economic and environmental analysis and comparison would assist in determining the overall feasibility of oxy-fuel combustion and its comprehensive sustainability characteristics.
ACKNOWLEDGEMENTS
The authors acknowledge the financial support of the Natural Sciences and Engineering Research Council of Canada.
References
- Beér, J. (2013). CO2 reduction and coal-based electricity generation. In Fossil Energy, pp. 475-488, Springer: New York. https://doi.org/10.1007/978-1-4614-5722-0_13
- Butcher, C. J. and Reddy, B. V. (2007). Second law analysis of a waste heat recovery based power generation system. Int. Journal of Heat and Mass Transfer, 50, 2355-2363. https://doi.org/10.1016/j.ijheatmasstransfer.2006.10.047
- Carazas, F. J. G., Salazar, C. H. and Souza, G. F. M. (2011). Availability analysis of heat recovery steam generators used in thermal power plants. Energy, 36(6), 3855–3870. https://doi.org/10.1016/j.energy.2010.10.003
- Carcasci, C. and Facchini, B. (2000). Comparison between two gas turbine solutions to increase combined power plant efficiency. Energy Conversion and Management, 41, 757-773. https://doi.org/10.1016/S0196-8904(99)00150-8
- Cenusa, V., Badea, A., Feidt, M. and Benelmir, R. (2004). Exergetic optimization of the heat recovery steam generators by imposing the total heat transfer area. Int. J. Thermodyn., 7, 149–156.
- Chen, L., Yong, S. Z. and Ghoniem, A. F. (2012). Oxy-fuel combustion of pulverized coal: Characterization, fundamentals, stabilization and CFD modeling. Progress in Energy and Combustion Science, 38(2), 156–214. https://doi.org/10.1016/j.pecs.2011.09.003
- Cihan, A., Hacıhafızoglu, O. and Kahveci, K. (2006). Energy–exergy analysis and modernization suggestions for a combined-cycle power plant. International Journal of Energy Research, 30, 115–126. https://doi.org/10.1002/er.1133
- de Gouw, J. A., Parrish, D. D., Frost, G. J. and Trainer, M. (2014). Reduced emissions of CO2, NOx, and SO2 from U.S. power plants owing to switch from coal to natural gas with combined cycle technology. Earth’s Future, 2(2), 75–82. https://doi.org/10.1002/2013EF000196
- El-Khattam, W. and Salama, M. M. A. (2004). Distributed generation technologies, definitions and benefits. Electric Power Systems Research, 71(2), 119-128. https://doi.org/10.1016/j.epsr.2004.01.006
- Feng, H., Zhong, W., Wu, Y. and Tong, S. (2014). Thermodynamic performance analysis and algorithm model of multi-pressure heat recovery steam generators (HRSG) based on heat exchangers layout. Energy Conversion and Management, 81, 282–289. https://doi.org/10.1016/j.enconman.2014.02.060
- Franco, A. and Russo, A. (2002). Combined cycle plant efficiency increase based on the optimization of the heat recovery steam generator operating parameters. International Journal of Thermal Sciences, 41(9), 843–859. https://doi.org/10.1016/S1290-0729(02)01378-9
- Ganapathy, V. (1996). Heat Recovery Steam Generators: Understand the Basics. Chemical Engineering Progress, August 1996, 32–35.
- Ganjehkaviri, A., Mohd Jaafar, M. N., Ahmadi, P. and Barzegaravval, H. (2014). Modelling and optimization of combined cycle power plant based on exergoeconomic and environmental analyses. Applied Thermal Engineering, 67(1–2), 566–578. https://doi.org/10.1016/j.applthermaleng.2014.03.018
- Ghazi, M., Ahmadi, P., Sotoodeh, A. F. and Taherkhani, A. (2012). Modeling and thermo-economic optimization of heat recovery heat exchangers using a multimodal genetic algorithm. Energy Conversion and Management, 58, 149–156. https://doi.org/10.1016/j.enconman.2012.01.008
- Karellas, S., Leontaritis, A. D., Panousis, G., Bellos, E. and Kakaras, E. (2013). Energetic and exergetic analysis of waste heat recovery systems in the cement industry. Energy, 58, 147–156. https://doi.org/10.1016/j.energy.2013.03.097
- Karthikeyan, R., Hussain, M., Reddy, B. V. and Nag P. K. (1998). Performance simulation of heat recovery steam generators in a cogeneration system. International Journal of Energy Research, 22, 399-410. https://doi.org/10.1002/(SICI)1099-114X(199804)22:5<399::AID-ER366>3.0.CO;2-Z
- Kuravi, S., Trahan, J., Goswami, D. Y., Rahman, M. M. and Stefanakos, E. K. (2013). Thermal energy storage technologies and systems for concentrating solar power plants. Progress in Energy and Combustion Science, 39(4), 285-319. https://doi.org/10.1016/j.pecs.2013.02.001
- Leduc, J., Mottaghi, M., Moran-Gonzalez, D., Sigler, E., Mahé, H. and Castel, J. (2011). Integration of a carbon capture-ready cogeneration plant: From requirements to design, facilities optimization and energy efficiency opportunities. Energy Procedia, 4, 2432–2439. https://doi.org/10.1016/j.egypro.2011.02.137
- Liang, X., Wang, Z., Zhou, Z., Huang, Z., Zhou, J. and Cen, K. (2013). Up-to-date life cycle assessment and comparison study of clean coal power generation technologies in China. Journal of Cleaner Production, 39, 24-31. https://doi.org/10.1016/j.jclepro.2012.08.003
- Mansouri, M. T., Ahmadib, P., Kaviric, A. G. and Jaafar, M. N. M. (2012). Exergetic and economic evaluation of the effect of HRSG configurations on the performance of combined cycle power plants. Energy Conversion and Management, 58, 47–58. https://doi.org/10.1016/j.enconman.2011.12.020
- Nag, P. K. and De, S. (1997). Design and operation of a heat recovery steam generator with minimum irreversibility. Appl. Therm. Eng., 17, 385–391. https://doi.org/10.1016/S1359-4311(96)00033-6
- Nord, L. O., Anantharaman, R. and Bolland, O. (2009). Design and off-design analyses of a pre-combustion CO2 capture process in a natural gas combined cycle power plant. International Journal of Greenhouse Gas Control, 3(4), 385–392. https://doi.org/10.1016/j.ijggc.2009.02.001
- Ong’iro, A., Ugursal, V. I., Al Taweel, A. M. and Walker, J. D. (1997). Modeling of heat recovery steam generator performance. Appl. Therm. Eng., 17, 427–446. https://doi.org/10.1016/S1359-4311(96)00052-X
- Rahim, M. A. (2012). Combined cycle power plant performance analyses based on the single-pressure and multipressure heat recovery steam generator. Journal of Energy Engineering, 138(3), 136–145. https://doi.org/10.1061/(ASCE)EY.1943-7897.0000063
- Rovira, A., Sánchez, C., Muñoz, M., Valdés, M. and Durán, M. D. (2011). Thermoeconomic optimisation of heat recovery steam generators of combined cycle gas turbine power plants considering off-design operation. Energy Conversion and Management, 52(4), 1840–1849. https://doi.org/10.1016/j.enconman.2010.11.016
- Shu, G., Liang, Y., Wei, H., Tian, H., Zhao, J. and Liu, L. (2013). A review of waste heat recovery on two-stroke IC engine aboard ships. Renewable and Sustainable Energy Reviews, 19, 385–401. https://doi.org/10.1016/j.rser.2012.11.034
- Toftegaard, M. B., Brix, J., Jensen, P. A., Glarborg, P. and Jensen, A. D. (2010). Oxy-fuel combustion of solid fuels. Progress in Energy and Combustion Science, 36(5), 581–625. https://doi.org/10.1016/j.pecs.2010.02.001
- Uchida, T., Yamada, T., Watanabe, S., Kiga, T., Gotou, T., Misawa, N. and Spero, C. (2013). Application and Demonstration of Oxyfuel Combustion Technologies to the Existing Power Plant in Australia. In Cleaner Combustion and Sustainable World, pp. 1385-1388. Berlin, Heidelberg: Springer. https://doi.org/10.1007/978-3-642-30445-3_184
- Valdes, M., Rovira, A. and Duran, M. D. (2004). Influence of the heat recovery steam generator design parameters on the thermoeconomic performances of combined cycle gas turbine power plants. Int. J. Energy Res., 28, 1243–1254. https://doi.org/10.1002/er.1026
- Wall, T., Liu, Y., Sperob, C., Elliott, L., Khare, S., Rathnam, R., Zeenathal, F., Moghtaderi, B., Buhre, B., Sheng, C., Gupta, R., Yamada, T., Makino, K. and Yu, J. (2009). An overview on oxyfuel coal combustion—State of the art research and technology development. Chemical Engineering Research and Design, 87(8), 1003–1016. https://doi.org/10.1016/j.cherd.2009.02.005
- Wall, T., Stangera, R. and Santos S. (2011). Demonstrations of coal-fired oxy-fuel technology for carbon capture and storage and issues with commercial deployment. International Journal of Greenhouse Gas Control, 5(1), S5–S15. https://doi.org/10.1016/j.ijggc.2011.03.014
- Wang, T., Zhang, Y., Peng, Z. and Shu, G. (2011). A review of researches on thermal exhaust heat recovery with Rankine cycle. Renewable and Sustainable Energy Reviews. 15(6), 2862–2871. https://doi.org/10.1016/j.rser.2011.03.015
- Wu, K. K., Chang, Y. C, Chen, C. H. and Chen, Y.D. (2010). High-efficiency combustion of natural gas with 21–30% oxygen-enriched air. Fuel, 89(9), 2455–2462. https://doi.org/10.1016/j.fuel.2010.02.002
- Yoshiie, R., Hikosaka, N., Nunome, Y., Ueki, Y. and Naruse, I. (2014). Effects of flue gas re-circulation and nitrogen contents in coal on NOX emissions under oxy-fuel coal combustion. Fuel Processing Technology. 136, 106-111. https://doi.org/10.1016/j.fuproc.2014.10.036
- Zheng, M., Reader, G. T. and Hawley, J. G. (2004). Diesel engine exhaust gas recirculation––a review on advanced and novel concepts. Energy Conversion and Management, 45, 883–900. https://doi.org/10.1016/S0196-8904(03)00194-8
How to cite this article
APA
Self, S. J., Rosen, M. A., & Reddy, B. V. (2018). Effects of Oxy-Fuel Combustion on Performance of Heat Recovery Steam Generators. European Journal of Sustainable Development Research, 2(2), 22. https://doi.org/10.20897/ejosdr/69787
Vancouver
Self SJ, Rosen MA, Reddy BV. Effects of Oxy-Fuel Combustion on Performance of Heat Recovery Steam Generators. EUR J SUSTAIN DEV RES. 2018;2(2):22. https://doi.org/10.20897/ejosdr/69787
AMA
Self SJ, Rosen MA, Reddy BV. Effects of Oxy-Fuel Combustion on Performance of Heat Recovery Steam Generators. EUR J SUSTAIN DEV RES. 2018;2(2), 22. https://doi.org/10.20897/ejosdr/69787
Chicago
Self, Stuart J., Marc A. Rosen, and Bale V. Reddy. "Effects of Oxy-Fuel Combustion on Performance of Heat Recovery Steam Generators". European Journal of Sustainable Development Research 2018 2 no. 2 (2018): 22. https://doi.org/10.20897/ejosdr/69787
Harvard
Self, S. J., Rosen, M. A., and Reddy, B. V. (2018). Effects of Oxy-Fuel Combustion on Performance of Heat Recovery Steam Generators. European Journal of Sustainable Development Research, 2(2), 22. https://doi.org/10.20897/ejosdr/69787
MLA
Self, Stuart J. et al. "Effects of Oxy-Fuel Combustion on Performance of Heat Recovery Steam Generators". European Journal of Sustainable Development Research, vol. 2, no. 2, 2018, 22. https://doi.org/10.20897/ejosdr/69787

 Full Text (PDF)
Full Text (PDF)