Abstract
Delimiting urban sprawl boundaries have been generally regarded as a regulatory policy measure to control chaotic and sparse urban expansion and for the protection of ecological areas towards sustainable development. The conservation of ecologically sensitive areas plays a key role in environmental protection; so, harmonizing urban sprawling with nature conservation can be viewed as a binary compatibility planning problem. This study aims to employ a geographical allocation model, based on the minimization of the environmental cost in order to apply complex spatial clustering techniques. Firstly, five ecological sensitivity factors affecting the ecological footprint of the study area are modeled through Geographic Information Systems (GIS) and Analytic Hierarchy Process (AHP) method in order to evaluate the Ecological Sensitivity Index. Then, several spatial objectives and constraints such as distance from the shoreline, continuity, and compactness are applied and finally, the most optimal areas are extracted for future urban sprawl. Spatial regulations, siting rules considerations and scenarios based on the parameters of the spatial clusters outputs are tested to the commune of Mytilene, located on Lesvos Island, Greece, where strong land use changes have been recorded by the urban sprawl over the last three decades.
License
This is an open access article distributed under the Creative Commons Attribution License which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Article Type: Research Article
EUR J SUSTAIN DEV RES, Volume 3, Issue 1, 2019, Article No: em0074
https://doi.org/10.20897/ejosdr/3975
Publication date: 06 Feb 2019
Online publication date: 14 Dec 2018
Article Views: 4859
Article Downloads: 2457
Open Access HTML Content References How to cite this articleHTML Content
INTRODUCTION
Nowadays, it is imperative to manage environmental protection in order to protect natural resources. We live in an era where the terms of sustainability and risk, expressing the relationship between human and nature, is an integral part of our daily lives and our duty is to ensure a balance between these two systems.
A crucial question is how the balance between human activities and environment in a sustainable manner can be measured? The evaluation of ecological importance at regional scale is to emphasize on the harmonious development between production space, living space and ecological space. Ecological risk assessment is conducted in order to transform scientific data into meaningful information about the risk of human activities to the environment. The purpose is to enable planners, risk managers, and stakeholders to make informed environmental decisions. A set of new technologies contributes in this direction, such as Geographic Information Systems (GIS) and Spatial Optimization models, which in combination with a broader set of disciplines can be a useful management tool to address the problem. Goal programming approaches, have many advantages compared to specific algorithms: simplicity of implementation if a programming software is available, reliability of the method, computational speed, exact or guaranteed approximate solution of the problem, and finally, possibility of easily modifying the model. The main purpose and contribution of this study are (1) to create a novel and integrated spatial index for evaluating and expressing the ecological sensitivity of a study area, (2) to demonstrate how the combination of theoretical models and GIS tools can contribute in environmental protection and land use management, (3) to develop a multi-objective land use allocation model for future urban sprawl boundaries expressed in a simple manner, and finally (4) to incorporate these models into a GIS platform in order to be able to achieve multiple future scenarios and filtering out solutions as an interactive operation during a planning process.
The present work is organized as follows: In Section 2 an extensive literature review is presented focusing on land use management and sustainable development using multiple criteria analysis and multi-objective optimization techniques. In Section 3, the methodological approach and all calculation rules and spatial tools we use are analyzed. In Section 4 the implementation of the proposed model is presented and the experimental results are discussed and finally, in Section 5 the conclusions of the present work are demonstrated with suggestions and directions for future research.
LITERATURE REVIEW
Environmental Protection and Land Use Management
Ecological importance evaluation towards the environmental protection is to explore the spatial distribution and provide measures for preventing ecological security issues from the regional development and construction (Xie et al., 2014). Among those measures developed for addressing cause-effect relationships relating the human and natural systems, the DPSIR (Driving Forces-Pressure-State-Impact-Response) has been established. In the DPSIR framework, there is a chain of causal links from ‘driving forces’ (human activities) over ‘pressures’ upon the environment (use and pollution) to environmental ‘state’ and ‘impacts’ on ecology and society finally leading to societal and political ‘responses’ (EEA, 1999). According to Spilanis et al. (2005, 1) “the construction of a practical tool for the maintenance and improvement of sustainability at a local level” is really important. To achieve that an operational definition of sustainable development through methods to monitor the present state of an area must be evolved and qualitative methods to pinpoint an area’s problems and their causes must be developed. Given a selected environmental issue (e.g ecological sensitivity) and a study area, the analysis along the DPSIR sequence can be simplified into four main steps: 1) determine which past (hindcasting), present or future human activities (forecasting) and needs are the driving forces of environmental and ecological changes by exercising anthropogenic pressures on an ecosystem (e.g. land use changes), 2) assess to which extend each driver/pressure contributes to changing the ecosystem by means of selected indicators that are representative for the ecosystem state (e.g. loss of biodiversity), 3) assess how those changes can impact natural systems and eventually human welfare and finally 4) develop management strategies and governance structures (response) for reducing or preventing undesired impacts (Nunneri, 2007).
Integrated analysis has already applied for ecological environment security assessment towards the sustainability measurement tools. Shao et al. (2013; 2014) and Cen et al. (2015) developed a model of indicator selection and quantitative assessment to ensure urban ecological security comprehensively and dynamically. The ecological evaluation based on GIS was firstly proposed by McHarg in the 1980s (McHarg, 1981) who mentioned the need for a model which allows the examination of the impact of any plan upon the health of the inhabitants and the well – being of the social and natural systems. A couple of decades later, Steiner, McHarg’s student, proposed a model of Environmentally Sensitive Areas (ESA) through a zonal planning that were regulated to offer an even higher level of protection (Steiner, 2000). In addition, Malczewski developed a multi-criteria method for the land suitability evaluation based on GIS (Malczewski, 2004). By 2010, Mingwu et al. (2010) applied two methods to analyze ecological sensitivity. Similar approaches specialized in urban ecological sensitivity evaluation system consisting four critical factors: a) vegetation, b) slope, c) elevation and d) rivers system (Huang et al., 2013) have been proposed as well as, on key factors of ecological sensitivity (e.g. geology, landform, hydrology, vegetation) (Yun et al. 2015).
Optimization and Land Use Allocation
Since land-use patterns are spatially explicit in nature, planning and management necessarily must integrate GIS, multi-criteria decision making and spatial optimization in meaningful ways if efficiency goals and objectives are to be achieved. In multi-objective optimization of land use (MOLU) models (Eastman et al., 1995; Aerts et al., 2003), the commonly used objectives include the improvements related to compatibility and dependency among neighboring land uses, the suitability score of land units according to specific indices, compactness, natural value of landscape, urban development potential etc. (Masoomi et al., 2012). In particular, it has been used in facility location problems (Church, 2002; Liu and Kao, 2010; Kratika et al., 2014; Eiselt and Marianov, 2015), ecological conservation models (Williams and ReVelle, 1996; Snyder et al., 2004; Costello and Polansky, 2004; Billionnet, 2013; Shao et al., 2015; Beyer et al., 2016;), suitability of land for agricultural use (Henseler et al., 2009; Hao et al., 2017), and regionalization problems and p-compact regions (Li et al., 2014; Kim et al., 2015).
Therefore, efforts have been made to produce computationally tractable solutions by using various optimization techniques like: 1) integer programming (Kao and Lin, 1996; Williams and ReVelle, 1998; Aerts et al., 2003; Shirable, 2005; Ligmann-Zielinska, 2008; Billionnet, 2012; Liu and Kao, 2012; Beyer et al., 2016), 2) heuristic methods based on a) genetic algorithms (Haque and Asami, 2011; Cao et al., 2012; Datta et al., 2012; Stewart and Janssen, 2014; Mohammadi et al., 2015), b) simulated annealing (Stewart et al., 2004; Aerts et al., 2005; Sante΄-Riveira et al., 2007) or c) particle swarm optimization (Liu et al., 2012; Masoomi et al., 2012; Sahebgharani, 2016). It is important to highlight that the adoption of integer linear programming methods in land use management has been slow as long as early trials, tests and models proved unsatisfactory. The main reason was the lack of computing power when the size of the problem is spatially expanding (Williams and ReVelle, 1998; Shirable, 2005; Beyer et al., 2016). Therefore, multiprocessing methods were applied to enforce IP model’s capability through parallel computing environment (Liu and Kao, 2012) and generative land-use modeling techniques enhanced with additional algorithms in order to solve the objectives faster (Ligmann-Zielinska et al., 2008). Contrary, heuristic algorithms are based on optimizing the objectives simultaneously in multi-objective mode focusing on Pareto front. Although, these methods do not generate an exact optimal solution, the generated solutions are meaningful and significant in many complex problems and case studies (Aerts et al., 2005).
Another important characteristic that characterizes MOLU is the structure of the input data and the ability the models have to interact with GIS. Many efforts have applied in recent years to combine spatial optimization procedures with GIS interfaces (Church, 2002; Sante Riveira et al., 2008; Chen et al., 2010; Cao et al., 2012; Sanussi et al., 2014; Stewart and Janssen, 2014; Mohammadi et al., 2015; Ligmann-Zielinska, 2017). GIS make use of two types of data: grid data (raster format) and attribute data (vector format). Data in a raster model are stored in a two-dimensional matrix of uniform cells on a regular grid. By their nature raster data are substantially easier to include in mathematical representations of the world for purposes of optimization. Using a grid-based representation of a planning region, Kao and Lin (1996), Stewart et al. (2004) and Janssen et al. (2008) showed that it was possible to formulate a spatial planning problem in mathematical terms and apply MOLU models to generate optimal solutions interactively.
Compactness, Contiguity and Spatial Constraints
Compactness and as a result contiguity is an issue that belongs to optimization spatial analysis which in turn applies diverse analytic and computational techniques in order to find optimal or near to optimal solutions (Vanegas et al., 2010). Land-allocation models in terms of the method used to encourage compactness and contiguity are separated within two types of constructs: solution-based and explicit constraint-based. The explicit constraint approach may be further divided into adjacency-based clustering, perimeter-based compactness, and block aggregation (Ligmann-Zielinska et al., 2008).
Numerous techniques have already been implemented in order to calculate compactness, but the most common and effective methods are: 1) with Integer Non-Linear Programming (INLP) (IP neighbor method) (Gabriel et al., 2006), 2) Integer Linear Programming (IP neighbor method) (Kao and Lin, 1996; Liu and Kao, 2013), 3) Linear IP using buffer zones cells (Williams and ReVelle, 1996), 4) Linear IP using aggregated blocks (Aerts et al., 2003; Stewart, 2004;) 5) Minimization of shape index (Cao et al., 2012) and finally 6) Spatial autocorrelation (Moran’s method) (Cao and Bo, 2010).
Contiguity can be explicitly structured in spatial optimization models or implicitly accounted for in a solution algorithm. Most explicit approaches are based on graph theory imposing network connectivity (Williams, 2002; Shirabe, 2005; Datta et al., 2012; Billionnet, 2013). Williams (2002) defined necessary and sufficient conditions for spatial connectivity. Rather than utilizing paths and spanning trees, Shirabe (2005) formulated contiguity constraints based on network flows. This work was extended by Duque et al. (2012) to include multiple network flows, one for each region. Datta et al. (2012) formalized their model as a multi-objective partitioning network problem using an Integer coded Genetic Algorithm.
Although, several models have been conducted and merely discussed, considering topological relations such us compactness and continuity, the generation of innovative mathematical algorithms will contribute to improve the efficiency of spatial optimization models able to balance accuracy and efficiency as well.
Urban Sprawl Management
Worldwide urbanization has brought dramatic changes to physical environment and human society, particularly in the developing countries and regions. The increasing demand for land resources due to growth in population, urban areas, and economy has posed great challenges to rural and urban sustainable development in regional or national scale worldwide. Most principles in sustainable land-use planning are spatial as discussed on previous sections, and GIS-coupled spatial optimization procedures are really important for planners, stakeholders and land owners in order to develop robust and easily handled approaches or lead to effective and sustainable decision support plans (Haque and Asami, 2014).
In recent years, great efforts have been succeeded on sustainable urban development and sprawl handling on the horizon of more compact and ecological friendly areas (Handayando et al., 2017). In particular, Kumar et al. (2016) with a Mixed Integer Quadratic Program (MIQP) consider just a single objective, maximizing suitability value of land to limit urban sprawl, based on two spatial constraints. Gabriel et al. (2006) on the contrary, take a multi-objective approach to controlling sprawl in land development by considering objectives from the perspective of the government, planners, environmentalists, conservationists, and land developers. Masoomi et al. (2012); Ma et al. (2017) and Handayando et al. (2017) include in their models similar objectives to achieve sustainable urban form areas based on maximum suitability for urban growth, maximum compactness and maximum preservation for high-quality farmlands combined with socio-economic quantitative criteria and constraints using an Ant Colony optimization algorithm.
Although, the most comprehensive framework, according to the literature review, to quantify and measure sprawl is implemented more than a decade ago by Ewing et al. (2002). Based on cause-effect relationships of urban sprawl and quality of life, includes numerous measures that are broadly divided into four categories, which are: a) residential density, b) neighborhood mixture of homes, jobs, and services, c) strength of centers, such as business districts, and d) accessibility to the street network. Finally, Ligmann-Zielinska et al. (2008) developed probably the most robust optimization model for efficient utilization of urban space. Their research employs Branch-and-Bound method to solve the resulting model. They use four objectives: 1) maximize the number of most attractive areas after open space allocation, 2) minimize redevelopment of urban areas through minimum possible resistance to change, 3) minimize incompatibilities between neighbored land uses and 4) minimize distance of new urban areas to already developed. Based on mathematical programming techniques and complex optimization procedures they highlight that their customized spatial optimization model is a promising method for generating land-use alternatives for further consideration in spatial decision-making.
MATERIALS AND METHODS
Study Area and Data
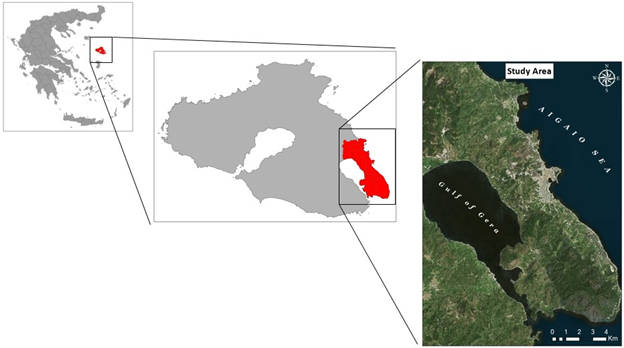
The study area is the greater area of Mytilene, which is located in Lesvos Island in North-East Aegean Sea in Mediterranean Sea (Figure 1). The municipality covers an area of 107.5 km2 with population of 37,890 inhabitants, according to the census of 2011. During the last three decades the land use changes regarding chaotic urban development lead to numerous impacts in the ecological and environmental status of the area. Data of land cover and ecosystem types were derived from the National Web Portal of Geospatial Data (http://www.geodata.gov.gr/) having the Corine LandCover 2000 dataset. This spatial information was further updated based on observations from satellite imagery and field work, as long as a lot of land use changes happened from 2000 to 2011. In order to create a detailed Digital Elevation Model (DEM) all the topographic elements (contours with interval of 4 meters, heights, roads and drainage network) were digitized from maps of 1:5000 scale of the National and Geographical Military service.
Ecological Sensitivity Model
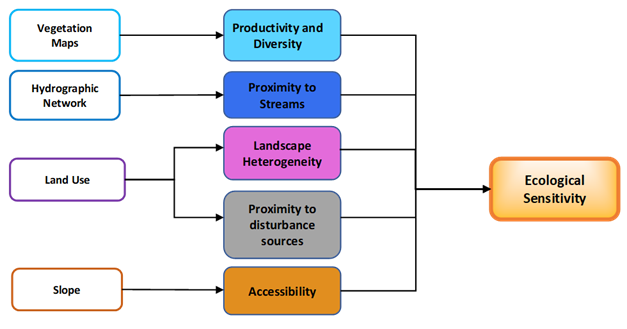
According to the related study of Troumbis (1995), the development of a mapping methodology assessing ecological sensitivity in natural systems, is an important condition to clarify the physical meaning of the term “ecological sensitivity”. The term of “sensitivity” is not a specific variable and does not describe any physical property of a living system. Also, it can’t be characterized by either as a single variable or as a complex descriptive parameter or factor which brings an etymological or conceptual dimension of the term “sensitivity”. On the other hand, it is more accurate if we say that it is described as a pressure factor on natural systems, derived from human activities and is defined as a quality attribute that refers to the changes in the productivity and diversity of a natural system (mainly due to the land use changes) (Figure 2).
Combining Ecological Sensitivity Model with GIS
The distinct steps of the framework are depicted in Figure 2. According to these steps the quantification of ecological sensitivity consists of: 1) Vegetation, 2) Drainage basin system, 3) Heterogeneity of ecological landscape, 4) Anthropogenic disturbance sources (e.g. settlements, transport networks) and 5) Topographic slope. The sensitivity grading scheme for each one of the above mentioned parameters, can be seen in Table 1. Each land-use type is the basic of the model regarding the expression of the productivity and the diversity of the system. The graded hierarchy of the different types of vegetation in relation to the productivity and diversity is achieved by using specific weighted values which reflect the system’s relative productivity and diversity amounts.
The other criteria are used to change – “affect” the initial value of vegetation’s specific gravity through the addition or subtraction of weight’s values. Therefore, the highest values correspond to the most diverse vegetation types which have a reliable water supply and are distant from sources of human disturbances. The lowest sensitivity values correspond to intensive agricultural areas, industrial and mining zones and settlements (Troumbis 1995). High ecological sensitive areas are expressed with negative values, ecological sensitive areas consist of values close to zero and non-ecological sensitive are expressed with positive values.
|
Table 1. Gradings of Sub-Criteria
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Optimization Model
Formulating an optimization problem generally contains three basic steps: defining decision variable(s), formulating objective function(s) and defining problem constraint(s). The optimization model is non-linear if the objective function and/or some of the constraints are non-linear. Moreover, Gabriel et al. (2006) highlight in their model the class of quadratic problems as part of non-linear problems, however, the relaxed version of these problems are simply convex, quadratic programs with linear constraints and thus represent a reasonable computational burden given the state of the art in optimization solvers. In order to solve multi-objective optimization problem two main processes can be applied in general, (1) the weighting method and (2) the constrained method (Gabriel et al., 2006). This spatial optimization routine is based on an Integer Non-Linear optimization Problem (INLP) and Branch and Bound algorithm upon linear constraints and weighted method approach, implemented through Gurobi optimization package (Gurobi Optimization, 2017). Each INLP contains 142555 quadratic objective terms, non-continuous variables, 202940 integer variables (202932 binary) and 6 constraints prioritizing the size of the total area and the handling of NoData values (e.g. to avoid solutions considered as NoData cell or to be able to search for optimal solutions in areas-cells that have common borders with NoData cells). All calculations were performed on a PC with 4G of RAM and an Intel Core Pentium processor running at 2.27 GHz.
Size, Data and Complexity of the Study Area
In this study, raster based formatted files are used (e.g. TIFF images) which are transformed into arrays as input for the optimization algorithm. Each raster cell represents ecological sensitivity index value and distance from the shoreline. Final raster files are masked based on already existing human activities (e.g. existing cities, industries, farmlands, quarries etc.) in order to avoid compatibility issues of the final optimal areas for future urban sprawl patterns. Therefore, the final datasets used as inputs for the model, contain 287.028 cells (603 rows * 476 columns) with a cell size of 30 meters.
Cluster’s compactness is affected by the neighborhood of each cell, while minimizing ecological sensitivity index and the distance from the shoreline. In particular, the neighborhood of a cell is expressed as the two-dimensional square lattice composed of a central cell and its four adjacent cells (Von Neumman Neighborhood) (Fotakis and Sidiropoulos, 2012). Among the total number of cells, NoData values of the raster file are not included but the model is capable to handle them in spite of the fact that these values do not participate in the final optimal solution. These types of cells can be borders, backgrounds, the sea or other data considered to not have valid values.
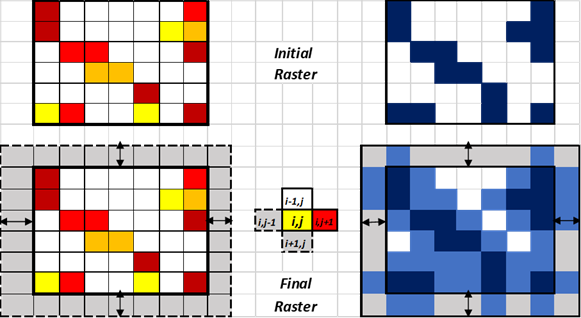
Finally, the model is customized in order to be able to search for an optimal solution near the boundary cells of the study area. Considering that the initial input raster is expressed as Ci,j (i the total number of rows and j the total number of columns), two additional pseudo-rows and pseudo-columns were added, forming a final raster dataset \(X_{i,j}\) for \(i = i + 2\) and \(j = j + 2\) as it is demonstrated in Figure 3.
Decision Variables, Objectives and Constraints
Minimum ecological sensitivity index (ES): Ecological sensitivity index is the first suitability factor of each land cell for future urban growth expansion as extracted from MCA analysis. Therefore, multiple factor model of weighted summation is applied to do the superposition calculation, ecological sensitivity index can be expressed by the following formula:
| \[ES = \sum_{i = 1}^{5}{w_{i}f_{i}}\] | (1) |
where \(\text{ES}\) is the ecological sensitivity index, \(w_{i}\) is the weight of each criteria \(i\) and \(f_{i}\) is the grading of criteria \(i\).
Minimum distance from the shoreline (D): The minimum distance from the shoreline is considered as optimal for future urban growth patterns. Therefore, considering socio-economic criteria, future urban areas near the shoreline are increasing quality of life as also they are closer to the most crucial human infrastructure networks (e.g. main road network, closer to the capital of the municipality and near to recreational activities)
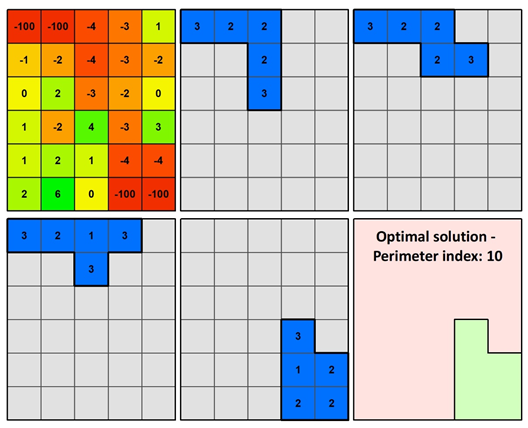
Maximum compactness of urban growth patterns (V): A customized approach is applied to calculate compactness and continuity of cells based on Kao and Lin (1996). In this study, compactness index is expressed as the total length of cluster cells’ edges that do not have common borders with any other cluster cell, leading the model to make urban patches regular and more rectangular. The continuity of the selected cells of the optimal solution is guaranteed because the model seeks to minimize fragmentation and calculate the smallest perimeter as Figure 4 presents.
Considering a hypothetical area of 30 cells Figure 4 demonstrates the alternatives and the optimal final solution regarding compactness, for a continuous cluster with size of 5 cells. The four optimal alternatives (minimized total sum) having a value of -211, must be further evaluated based on their compactness. As mentioned above, the most compact cluster is the one with the smallest perimeter which is calculated by the free edges of all cells. Therefore, the first three scenarios (blue color areas) have a cluster perimeter equal to 12, while the fourth is equal to 10 and is the optimal solution.
Multiple factors optimization: For an optimization problem with multiple factors, the objective function of the model should be modified adding the weight factor of each objective and can be expressed as:
| \[\text{Minimize} = \sum_{i = 1}^{I}{\sum_{j = 1}^{J}\left\lbrack x_{\text{ij}}*\left( w_{\text{es}}*ES_{\text{ij}} + w_{d}*D_{\text{ij}} + w_{v}*V_{\text{ij}} \right) \right\rbrack}\] | (2) |
where:
| \[V_{\text{ij}} = 4 - \left( x_{i,j - 1} + x_{i,j + 1} + x_{i - 1,j} + x_{i + 1,j} \right)\] | (3) |
where \(I\) and \(J\) are the total number of rows and columns; \(w_{v}\) is the weight for compactness, \(w_{d}\) is the weight for distance from the shoreline features and \(w_{\text{es}}\) is the weight for Ecological Sensitivity index. For each cell \(\text{ij}\), \(ES_{\text{ij}}\) represents the value of \(\text{ES}\) (Eq. 1), \(D_{\text{ij}}\) represents the value of the distance from the shoreline and \(V_{\text{ij}}\) represents the total cell edges contribute to cluster perimeter; \(x_{\text{ij}}\) is a binary variable (0 or 1) to represent whether the cell \(\text{ij}\) belongs to final cluster or not.
Optimization constraints: The two fundamental constraints for the optimization model refer indirectly to (Eq. 4) compactness calculation and neighbors accounting, NoData cell values handling and (Eq. 5) number of total amount of selected cells by the user, in order to calculate the objectives.
| \[\sum_{i = 1}^{I}{\sum_{j = 1}^{J}x_{i,\ j}} = N\] | (4) |
subject to:
\(N\) as total cells selected for Urban Sprawl boundaries development for \(\forall I \in \left\{ 0,\ldots,i + 1 \right\}\); \(\forall J \in \left\{ 0,\ldots,j + 1 \right\}\)
| \[\sum_{i = 1}^{K}{\sum_{j = 1}^{L}x_{i,\ j}} = N\] | (5) |
subject to:
\(N\) (total cells) for \(\forall K \in \left\{ 1,\ldots,i \right\}\); \(\forall L \in \left\{ 1,\ldots,j \right\}\)
where:
\(N\) is the required size (in numbers of cells) of the desired site.
RESULTS AND DISCUSSION
Sub–Criteria for Ecological Sensitivity Index Calculation
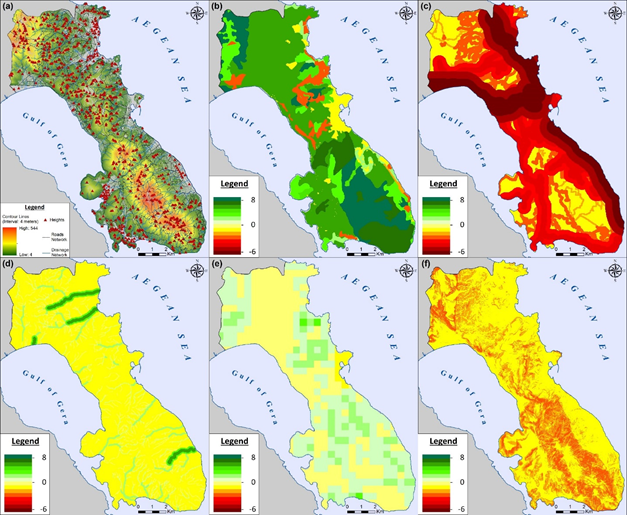
The primary data used (contour lines, elevation points, drainage and road network) in order to create Digital Elevation Model (DEM) and to calculate sub-criteria gradings are presented in Figure 5(a). In particular:
Productivity and Diversity index Figure 5(b): The most downgraded land units are observed in the central part of the study area as also to the South – East coastal part where urban sprawl areas and other individual industries are located. Contrary, the most productive areas are observed in North –West and South – East part of the study area where different types of forests, wetlands and sclerophyll vegetation exist.
Proximity to disturbance sources index Figure 5(c): The higher disturbance values exist because of the small highways that connect the city of Mytilene with the entire island (North, South and Western part) as also the regional road network of the municipality that connects the different smaller settlements with the capital of Lesvos island covering the biggest part of the study area.
Proximity to streams index Figure 5(d): The drainage network was divided in different classes according to Stahler’s method of designating stream orders (Strahler, 1957). The biggest the stream order and the proximity is, the higher values of the index are observed, mostly to the North and South mountainous areas of Kapodistrian municipality.
Landscape Heterogeneity index Figure 5(e): Landscape diversity calculated to study the local landscape heterogeneity by drawing out a grid of 500 m cell size and dimensions of 38*29 cells. Heterogeneity index reflects the diversity of the amounts of landscape elements, apart from areas with continuous urban development and the variation of their proportion. The higher the combination of different vegetation types is observed the less vulnerable is an ecosystem as long as the ecological footprint increases. Less sensitive areas are observed to the South part of the study area where Amali mountain is located.
Accessibility index Figure 5(f): Higher slope values reduce ecosystem’s regenerative potential as long as the capability of humans to intervene (e.g. forest fires) is decreased. The most vulnerable areas are observed to the North-West and South – East part of the municipality where higher elevation values are observed.
Weight Determination and Ecological Sensitivity Index
As ecological sensitivity is a multi-attribute index, it often requires a method combining qualitative and quantitative analysis to evaluate. The analytical hierarchy process (AHP) is a decision-making method and a theory of measurement through pairwise comparisons and relies on the judgements of experts to derive priority scales. In the AHP method, obtaining the weights or priority vector of the alternatives or the criteria is required. The decision-making process starts with defining and dividing the problem into issues-criteria, which may optionally be divided further to form a hierarchy of issues-elements (Saaty 2008).
According to the calculation results derived from AHP, as shown in Table 2, the pairwise comparison matrix is deemed to have the satisfactory consistency having a value CR = 0.059 < 0.1 (CI = 0.067 and RI = 1.12 for n = 5, Boroushaki and Malczewski (2008); Saaty (2012).
|
Table 2. Pair-wise comparison matrix and consistency index
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
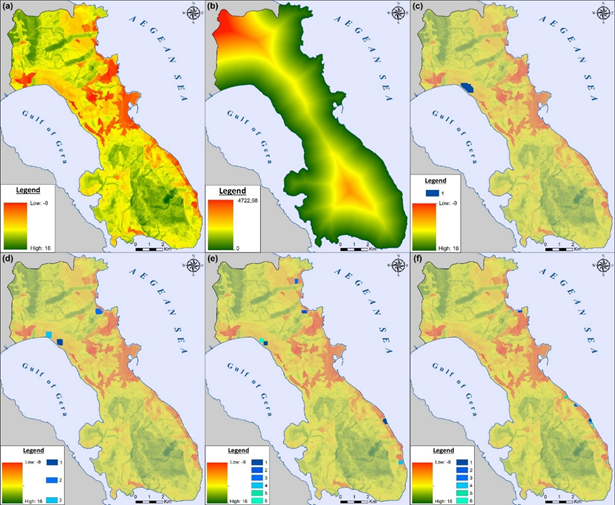
The last step is to transform the ecological sensitivity and distance from the shoreline single factor layers into the final raster maps. The final results are presented in Figure 6(a-b) noticing that the scale of the cell values for ES ranges between -9 and 16, as a result, most downgraded areas are expressed with red and orange colors. Contrary, the most ecologically upgraded and stable areas are visualized with different green shades.
Urban Sprawl Boundaries Results
Final results of Ecological Sensitivity index, Distance from the shoreline and all future urban sprawl areas are presented in Figure 6. The initial values for ES range from -9 for more sensitive areas to 16 for less sensitive (Figure 6-a) and the Distance from the shoreline in meters, using Euclidean metric (Figure 6-b), can exceed almost 5000 meters. Next step consists of the masking of non-available areas for future urban sprawl development due to incompatibility issues with already existing urban, suburban, industrial, agricultural and high natural value forest areas. Final ES and Distance metric values range from -3 to 13 and up to 4500 meters accordingly. Based on the masked results for the two criteria, final score values are rescaled to a common scale ranging from 0 to 4 and optimization model is set up.
All scenarios of future urban growth patterns are presented in Figure 6 (c-f) for total number of selected cells N = 50, 100, 250 and 500. Results show that the final areas are continuous, compact and in some cases absolutely rectangular as the total number of selected cells decreases. Moreover, by overlaying the final clusters’ results with ES is noticed that optimal patterns are concentrated to the areas with accordingly the lowest ES value and near the shoreline.
Results Analysis and Discussion
To validate the performance of the proposed model on future compact urban sprawl site prospecting, multiple tests are applied. Four different patterns’ allocation scenarios were performed to determine and analyze the optimal solutions and the results show identical optimal regions.
In particular, the size and the amount of ‘the total areas’ (Number of cells and Number of Clusters) is examined, weighting factors for each objective and different gap values to obtain global and local optimum regarding the Pareto front. Considering the objectives and constraints designed in the INLP model, Pareto analysis for the three criteria considered and final results are categorized and analyzed into three parts as it is demonstrated in Table 3: (1) performance regarding runtime characteristics of the model to find global and local optimum solutions, (2) ability to obtain connected and compact patterns; and (3) performance on leading to fragmentation issues based on weights criteria sensitivity.
The three objectives (i.e. minimum ES, minimum perimeter and minimum distance from the shoreline) do not seem to conflict with each other, although, the user must pay attention regarding the compactness weight sensitivity in order to avoid fragmentation issues. The values of the weight for each objective ranging from 0 to 1 can be set, and various combinations can be generated to analyze the sensitivity of the proposed model. The composite optimality score can be defined in different ways by emphasizing different weights to generate alternative patterns.
Sensitivity analysis was carried on mainly for the perimeter criterion minimization as Figure 7(A-F) demonstrates given the fact that the other two objectives do not seem to have remarkable negative impact to the final result. In Figure 7(A) is considered a compactness weight of 0.1 in the scale from 0 to 1 and we observe that as the objectives’ weight remains low, final areas are fragmented. In Figure 7(B-F) is presented how fragmentation is eliminated leading to one final compact cluster by increasing compactness weight by 0.1 for each test. Therefore, applying a compactness weight of 0.5 continuity and perimeter minimization is guaranteed, issue that is reflected to the final results as they analyzed on Table 3 where is noticed that fragmentation issues are observed for weighting factors below 0.25 – 0.6 according to the clusters’ size. As the number of the total cells N increases a higher compactness weight must be applied in order to guarantee continuity and eliminate fragmentation, although for smaller areas the equivalent weight decreases to values near 0.3.
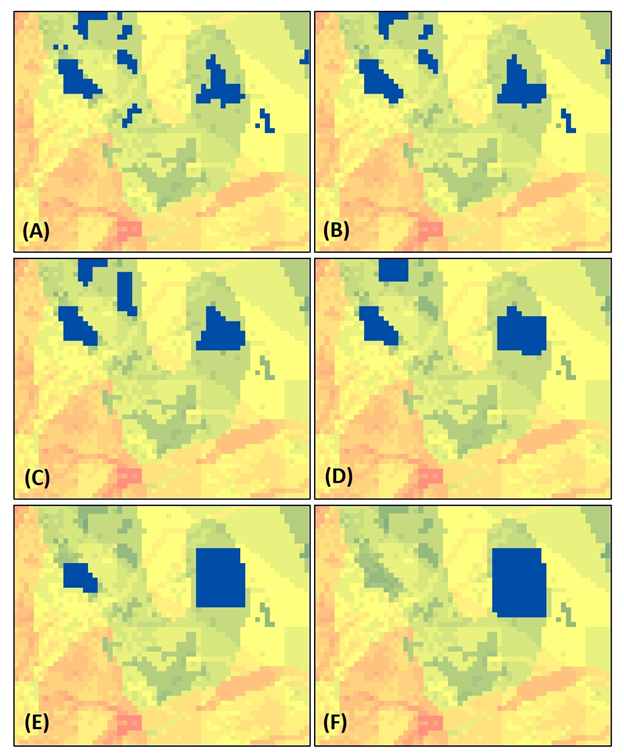
Another important factor that explains considerably how the algorithm works regarding perimeter minimization is the standard deviation of the values of the participant objectives. As the differences between the values of each objective increase, compactness weight remains low, contrary when the differences consist of small fluctuations for each objective the compactness weight increase.
Analyzing further the final results, different weight combinations show that the weight for suitability ranging from 0.2 to 0.4, weight for distance from the shoreline ranging from 0.15 to 0.4, and weight for compactness approximated from 0.4 to 0.6 are rational for application. For small patterns (N=50) model returns absolutely squared areas irrespective of each criteria’s weight. Searching for larger areas (e.g. N= 250 and 500) it is highlighted that as long as compactness weighting factor is maximized (>=0.6) contiguity and compactness are guaranteed. Although, is noted that for large clusters as compactness weight reduces (<=0.6), final optimal areas might be fragmented (e.g. in two separate clusters), something that seems normal considering that contiguity and compactness are expressed through the objective function and not as constraint factors.
Moreover, additional tests were applied to compare final results quality and the impact to the final runtime response when local and not global optimum solutions were obtained by customizing the model’s gap value from 99. 5 % (e.g. gap value = 0.005) to 90% of the optimal solution (e.g. gap value = 0.1). The INLP achieves promising results with respect to both solution quality (how close it is to optimality) and processing time over a range of problem sizes highlighting an impressive reduction to the total runtime of the algorithm.
As it is observed a processing time of approximately 30 minutes was required for one cluster to achieve a solution within 99.5% of optimality, while achieved solutions within 90% of optimality within 90 seconds. Moreover, processing time reduction for three clusters is remarkable from 6 hours to near 20 minutes. Regarding compactness weight sensitivity for scenario 1 and 2 it is observed that a value above 0.6 guarantees contiguity and eliminates fragmentation. For the last two scenarios is observed a reduction regarding the processing time as also to the compactness weight index. This highlights that the model output is not sensitive to the reduction of constraint conditions (number of total cells) regarding the total runtime of the model, nevertheless, a compactness weight increase, affects the final processing time of the algorithm. By reducing the gap to 90%, the summary results seem to have a similarity in the optimal regions obtained with a gap of 99.5% and in some cases (Scenario 3) the final optimal values of ES are exactly the same. For scenario 1 and 2 respectively small changes are observed to the final compactness of the selected patterns. This indicates a consistency in the determination of optimal regions (decision variables) by the zero-one integer programming model.
From the analysis of the results presented in Table 3 and the screening analysis (map representation) in Figure 6 the advantages and limitations of the proposed model can be further discussed. Most crucial characteristics of the INLP model is that allocates the best possible solutions in a limited amount of time using one simple constraint as long as all crucial parameters are optimized through the objective function in a simple and easily customized manner. Beyer et al. (2016) indicate, as the advances in algorithms and processing power increases, integer linear and non-linear programming has become a flexible and efficient framework for identifying optimal solutions to conservation planning problems and future applications could adopt multi-objective optimization approaches in which a set of objective functions must be minimized (or maximized) and the targets are implemented as objectives, not constraints. Therefore, treating constraints as objectives in a multi-objective optimization framework would allow decision-makers to more fully explore the solution space by explicitly evaluating the importance and consequences of trade-offs among objectives. Based on the above, it can be declared that the proposed model highlights the effectiveness of Integer Programming regarding the time consumption and the solution quality as long as the structure of the objective functions (especially compactness calculation) and the simple constraints expressions lead to a robust optimization algorithm for land use management issues.
|
Table 3. Results analysis and scenarios evaluation
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Additionally, another advantage of the proposed framework is focusing on the size of the spatial units that are optimized (near 300.000 cells) considering that mathematical formulations targeted to the location of contiguous and compact sites are applied in problems with sizes ranging from 100 to 4900 units. According to Vanegas et al. (2010) mathematical approaches must be applied even to larger regions when they are represented by an appropriate number of units and since compactness modeled by means of mathematical programming require a high amount of computational resources to achieve optimal solutions, the proposed model seems to constitutes a robust spatial optimization tool to numerous classes of land use management problems.
Finally, considering compactness calculation, fragmentation minimization and raster-based spatial optimization approaches research has demonstrated that spatial connectivity objectives appear to be difficult to model and solve through its highly non-linear formulations (Kao and Lin, 1996; Aerts et al., 2005), issue that seems to be effectively overcome in the proposed model using the appropriate weighting scales and applying all spatial criteria to the objective function. Kumar et al. (2016) notice that, given the amount of time it takes to solve an ILP or INLP, there is a limit on the number of factors that can be incorporated into an experiment. In the current approach, it is noticed that as the objectives increase and the feasible solutions are eliminated the total runtime for each scenario is minimized and the most crucial factor that affects the time consumption to achieve optimal solution is the compactness weight.
CONCLUSION AND FUTURE RESEARCH
Spatial delimitation and prospecting of compact future urban sprawl areas is a complex decision problem based on multiple planning demands, objectives and regulations. The proposed spatial optimization model was tested in the core area of Kapodistrian municipality in Lesvos island upon real datasets and spatial information based on the analytical expression of ecological sensitivity quantification, indicating that optimal future suburban patterns can be efficiently derived from the proposed algorithm. This study highlights how an INLP algorithm can handle irrespectively the trade-off between critical environmental indices and human interventions exploiting location allocation and siting procedures, GIS and spatial optimization techniques. The main modifications include: (1) a different measure for assessing ecological sensitivity; (2) the implementation of a novel approach for formatting and calculating compactness index and finally, (3) the integration of these aspects through a fast and easily handled GIS - model based on Integer Non-Linear programming and multi-objective spatial optimization routines.
The results demonstrate the effectiveness, the efficiency and the potential of the proposed model on supporting urban planning and decision-making processes representing absolutely optimal solutions according to the planner’s preferences in a limited amount of time. Therefore, the proposed framework could help both planners and stakeholders in considering the relations among environmental growth and future urban sprawl sustainability using simple implementation tools and objectives avoiding complex spatial algorithms. Furthermore, it relies on a rigorous and systematic mathematical formulation that avoids falling in sub-optimal solutions leading to optimal contiguous and compact sites seeking to highlight that with the current advances in algorithms, solvers and processing power development, integer linear and non-linear programming has become a flexible and efficient framework for identifying realistic solutions to conservation planning problems. Although developed primarily for land use management, the proposed framework can be applied to any particular region as a powerful tool for site selection problems and location allocation issues in the field of sustainable land and marine environmental management.
Finally, future research consists of additional siting objectives and constraints in order to extend model’s capability to re-produce optimal patterns from national to regional and local level, implementation of fuzzy logic techniques upon the gradings of the sub-criteria, using additional programming techniques towards the scope of producing a fully compatible toolbox and a spatial management tool for GIS platforms.
References
- Aerts, J. C. J. H., Eisinger, E., Heuvelink, G. B. M. and Stewart T. J. (2003). Using Linear Integer Programming for Multi-site Land-use Allocation. Journal in Geographical Analysis, 35, 148–169. https://doi.org/10.1111/j.1538-4632.2003.tb01106.x
- Aerts, J. C. J. H., Herwijnen, M. V., Janssen, R. and Stewart, T. J. (2005). Evaluating Spatial Design Techniques for Solving Land-use Allocation Problems. Journal of Environmental Planning and Management, 48(1), 121-142. https://doi.org/10.1080/0964056042000308184
- Beyer, H. L., Dujardin, Y., Watts, M. E. and Possingham, H. P. (2016). Solving conservation planning problems with integer linear programming. Journal in Ecological Modelling, 328, 14-22. https://doi.org/10.1016/j.ecolmodel.2016.02.005
- Billionnet, A. (2012). Designing an optimal connected nature reserve. Journal in Applied Mathematical Modeling, 36, 2213-2223. https://doi.org/10.1016/j.apm.2011.08.002
- Billionnet, A. (2013). Mathematical optimization ideas for biodiversity conservation. Journal in European Journal of Operational Research, 231, 514-534. https://doi.org/10.1016/j.ejor.2013.03.025
- Boroushaki, S. and Malczewski, J. (2008). Implementing an extension of the analytical hierarchy process using ordered weighted averaging operators with fuzzy quantifiers in ArcGis. Computers & Geosciences, 34(4), 399-410. https://doi.org/10.1016/j.cageo.2007.04.003
- Cao, K. and Bo H. (2010). Comparison of Spatial Compactness Evaluation methods for Simple Genetic Algorithm based Land Use Planning Optimization problem. The International Archives of the Photogrammetry. Journal in Remote Sensing and Spatial Information Sciences, vol, Part II.
- Cao, K., Huang, B., Wang, S. and Lin, H. (2012). Sustainable land use optimization using Boundary-based Fast Genetic Algorithm. Journal in Computers, Environment and Urban Systems, 36, 257–269. https://doi.org/10.1016/j.compenvurbsys.2011.08.001
- Cen, X., Wu, C., Xing, X., Fang, M., Garang, Z. and Wu, Y. (2015). Coupling Intensive Land Use and Landscape Ecological Security for Urban Sustainability: An Integrated Socioeconomic Data and Spatial Metrics Analysis in Hangzhou City. Journal in Sustainability, 7, 1459-1482. https://doi.org/10.3390/su7021459
- Church, R. L. (2002). Geographical information systems and location science. Journal in Computers and Operations Research, 29, 541–562. https://doi.org/10.1016/S0305-0548(99)00104-5
- Costello, C. and Polansky, S. (2004). Dynamic reserves site selection. Journal in Resource and Energy Economics, 26, 157-174. https://doi.org/10.1016/j.reseneeco.2003.11.005
- Datta, D., Malczewski, J. and Figueira, J. R. (2011). Spatial aggregation and compactness of census areas with a multiobjective genetic algorithm: A case study in Canada. Environment and Planning B: Planning and Design, 39, 376-392. https://doi.org/10.1068/b38078
- Duque, J. C., Anselin, L. and Rey, S. J. (2012). The max-p-regions problem. Journal of Regional Science, 52, 397–419. https://doi.org/10.1111/j.1467-9787.2011.00743.x
- Eastman, J. R., Jin, W., Kyem, P. A. K. and Toledano, J. (1995). Raster procedures for multi-criteria/multi-objective decisions. Journal in Photogrammetric Engineering and Remote Sensing, 61, 539–547.
- EEA. (1999). Environmental Indicators: Typology and Overview. European Environmental Agency, 19.
- Eiselt, H. A. and Marianov, V. (2015). Location modeling for municipal solid waste facilities. Journal in Computers and Operations Research, 62, 305-315. https://doi.org/10.1016/j.cor.2014.05.003
- Ewing, R., Pendal, R. and Chen, D. (2002). Measuring sprawl and its impact. Technical Report Smart Growth America, Washington D.C.
- Fotakis, D. and Sidiropoulos, E. (2012). Combined land-use and water allocation planning. Journal in Annals of Operations Research, 219(1), 169-185. https://doi.org/10.1007/s10479-012-1080-y
- Gabriel, S. A., Faria, J. A. and Moglen, G. E. (2006). A multi-objective approach to smart growth in land development. Journal in Socio-Economic Planning Sciences, 40, 212-248. https://doi.org/10.1016/j.seps.2005.02.001
- Gurobi Optimization, Inc. Gurobi Optimizer Reference Manual Version 7.5./Gurobi Optimizer Version 7.5.2. Houston, Texas: Gurobi Optimization, Inc. (2017). Software program. Houston, Texas: Gurobi Optimization.
- Janssen, R., van Herwijnen, M., Stewart, T. J. and Aerts, J. C. J. H. (2008). Multiobjective decision support for land use planning. Environment and Planning B: Planning and Design, 35, 740-756. https://doi.org/10.1068/b33071
- Janssen, R., Arciniegas, G. A. and Verhoeven, J. T. A. (2013). Spatial evaluation of ecological qualities to support interactive design of land use plans. Environment and Planning B: Planning and Design, 40, 427-446. https://doi.org/10.1068/b37064
- Hammad, A. W. A., Akbarnezhad, A. and Rey, D. (2016). A multi-objective mixed integer nonlinear programming model for construction site layout planning to minimize noise pollution and transport costs. Journal in Automation in Construction, 61, 73-85. https://doi.org/10.1016/j.autcon.2015.10.010
- Handayanto, R. T., Tripathi, N. K., Kim, S. M. and Guha, S. (2017). Achieving a Sustainable Urban Form through Land Use Optimisation: Insights from Bekasi City’s Land-Use Plan (2010–2030). Sustainability, 9, 221. https://doi.org/10.3390/su9020221
- Hao, L., Su, X., Singh, V. P. and Ayantobo, O. O. (2017). Spatial Optimization of Agricultural Land Use Based on Cross-Entropy Method. Entropy, 19, 592. https://doi.org/10.3390/e19110592
- Haque, A. and Asami, Y. (2014). Optimizing urban land use allocation for planners and real estate developers. Journal in Computers, Environment and Urban Systems, 46, 57-69. https://doi.org/10.1016/j.compenvurbsys.2014.04.004
- Henseler, M., Wirsig, A., Herrmann, S. Krimly, T. and Dabbert, S. (2009). Modeling the impact of global change on regional agricultural land use through an activity-based non-linear programming approach. Agricultural Systems, 100, 31–42. https://doi.org/10.1016/j.agsy.2008.12.002
- Huang, T., Cheng, S. G. and Hu, Z. X. (2013). The Urban Ecological Sensitivity Analysis of Enshi city Based on GIS and Analytic Hierarchy Process Model. Advanced Materials Research, 671–674, 2599–2603. https://doi.org/10.4028/www.scientific.net/AMR.671-674.2599
- Kao, J. J. and Lin, H. Y. (1996). Multifactor Spatial Analysis for Landfil Siting. Journal of Environmental Engineering, 122(10), 902-908. https://doi.org/10.1061/(ASCE)0733-9372(1996)122:10(902)
- Kim, K., Dean, D. J., Kim, H. and Chun, Y. (2015). Spatial optimization for regionalization problems with spatial interaction: a heuristic approach. International Journal of Geographical Information Science. https://doi.org/10.1080/13658816.2015.1031671
- Kratikca, J. Dugošija, D. and Savic΄, A. (2014). A new mixed integer linear programming model for the level uncapacitated facility location problem. Journal in Applied Mathematical Modelling, 38, 2118-2129. https://doi.org/10.1016/j.apm.2013.10.012
- Kumar, P., Rosenberger, J. M. and Daud Iqbal, G. M. (2016). Mixed integer linear programming approaches for land use planning that limit urban sprawl. Journal in Computers and Industrial Engineering, 102, 33-43. https://doi.org/10.1016/j.cie.2016.10.007
- Li, W., Church, R. L. and Goodchild, M. F. (2014). An extendable heuristic framework to solve the p-compact-regions problem for urban economic modeling. Journal at Computers, Environment and Urban Systems, 43, 1-13. https://doi.org/10.1016/j.compenvurbsys.2013.10.002
- Ligmann-Zielinska, A., Church, R. L. and Jankwski, P. (2008). Spatial optimization as a generative technique for sustainable multiobjective land-use allocation. International Journal of Geographical Information Science, 22(6), 601-622. https://doi.org/10.1080/13658810701587495
- Liu, K. H. and Kao, J. J. (2012). Parallelized branch-and-bound algorithm for raster-based landfill siting. Journal in Civil Engineering and Environmental Systems, 30(1), 15-25. https://doi.org/10.1080/10286608.2012.709504
- Liu, Y., Wang, H., Ji, Y., Liu, Z. and Zhao, X. (2012). Land Use Zoning at the County Level Based on a Multi-Objective Particle Swarm Optimization Algorithm: A Case Study from Yicheng, China. International Journal of Environmental Research and Public Health, 9, 2801-2826. https://doi.org/10.3390/ijerph9082801
- Ma, S., Li, X. and Cai, Y. (2017). Delimiting the urban growth boundaries with a modified ant colony optimization model. Computers, Environmental and Urban Systems, 62, 146-155. https://doi.org/10.1016/j.compenvurbsys.2016.11.004
- Malczewski, J. (2004). GIS-based land-use suitability analysis: a critical overview. Progress in Planning, 62, 3–65. https://doi.org/10.1016/j.progress.2003.09.002
- Masoomi, Z., Mesgari, M. S. and Hamrah, M. (2013). Allocation of urban land uses by Multi-Objective Particle Swarm Optimization algorithm. International Journal of Geographical Information Science, 27(3), 542-566. https://doi/org/10.1080/13658816.2012.698016
- McHarg, I. L. (1981). Human ecological planning at Pensylvania. Landscape Planning, 8, 109–120. https://doi.org/10.1016/0304-3924(81)90029-0
- Mingwu, Z., Haijiang, J., Desuo, C. and Chunbo, G. (2010). The comparative study on the ecological sensitivity analysis in Huixian karst wetland, China. International Society for Environmental Information Sciences, Annual Conference (ISEIS). https://doi.org/10.1016/j.proenv.2010.10.043
- Nunneri, C. (2007). Linking Ecological and Socio-economic Systems Analysis – A methodological approach based on Ecological Risk. Berichte aus dem Forschungs- und Technologiezentrum Westküste, No. 45, Büsum 2007.
- Saaty, T. L. (2008). Decision making with the analytic hierarchy process. International Journal of Services Sciences, 1(1), 83. https://doi.org/10.1504/IJSSCI.2008.017590
- Saaty, T. L. (2012). Decision Making for Leaders: The Analytic Hierarchy Process for Decisions in a Complex World. Third Revised Edition. Pittsburgh: RWS Publications.
- Sahebgharani, A. (2016). Multi-Objective Land Use Optimization through Parallel Particle Swarm Algorithm: Case Study Baboldasht District of Isfhan, Iran. Journal of Urban and Environmental Engineering, 10(1), 42-49. https://doi.org/10.4090/juee.2016.v3n1.042049
- Sante΄-Riveira, I., Boullo΄n-Maga΄n, M., Crecente-Maseda and Miranda-Barro΄s, D. (2008). Algorithm based on simulated annealing for land-use allocation. Journal in Computers and Geosciences, 34, 259-268.
- Shao, C., Tian, X., Guan, Y., Ju, M. and Xie, Q. (2013). Development and Application of a New Grey Dynamic Hierarchy Analysis System (GDHAS) for Evaluating Urban Ecological Security. Journal in International Journal of Environmental Research and Public Health, 10, 2084-2108. https://doi.org/10.3390/ijerph10052084
- Shao, C. et al. (2014). Trends Analysis of Ecological Environment Security based on DPSIR Model in the Coastal zone: A survey study in Tianjin, China. Int. J. Environ. Res, 8(3), 765-778.
- Shao, J., Yang, L., Peng, L., Chi, T. and Wang, X. (2015). An Improved Artificial Bee Colony-Based Approach for Zoning Protected Ecological Areas. PLoS ONE, 10(9), e0137880. https://doi.org/10.1371/journal.pone.0137880
- Snyder, S. A., Haight, R. G. and ReVelle, C. S. (2004). A scenario optimization model for dynamic reserve site selection. Journal in Environmental Modeling and Assessment, 9, 179-187. https://doi.org/10.1023/B:ENMO.0000049388.71603.7f
- Spilanis, I., Kizos, T., Kondili, J., Koulouri, M. and Vakoufaris, H. (2005). Sustainability measurement in islands: The case of South Aegean Island, Greece. Biodiversity Conservation and Sustainable Development in Mountain Areas of Europe, Conference, Greece, Ioannina, 20-24 September.
- Steiner, F. (2000). A watershed at a watershed: the potential for environmentally sensitive area protection in the upper San Pedro Srainage Basin (Mexico and USA). Landscape Urban Plann, 129–148.
- Stewart, T. J., Janssen, R. and van Herwijnen, M. (2004). A genetic algorithm approach to multiobjective land use planning. Computers and Operations Research, 32, 2293-2313. https://doi.org/10.1016/S0305-0548(03)00188-6
- Troumbis A. (1995). Ecological networks in Greece: Current status, administration approaches and research initiatives. Landschap, 12(3), 51-62.
- Williams, J. C. and ReVelle, C. S. (1996). A 0-1 programming approach to delineating protected reserves. Journal in Environment and Planning B: Planning and Design, 23, 607-624. https://doi.org/10.1068/b230607
- Vanegas, P., Cattrysse, D. and Orshven, J. V. (2010). Compactness in Spatial Decision Support: A Literature Review, D. Taniar et al. (Eds.): ICCSA 2010, Part I, LNCS 6016, Springer – Verlag Berlin Heidelberg, 414-419.
- Vaskan, P., Passuello, A., Gosalbez, G. G. and Schumacher, M. (2013). Combined use of GIS and mixed-integer linear programming for identifying optimal agricultural areas for sewage sludge amendment: A case study of Catalonia. Journal in Environmental Modelling and Software, 46, 163-169. https://doi.org/10.1016/j.envsoft.2013.03.007
- Xie, H., Yao, G. and Liu, G. (2014). Spatial evaluation of the ecological importance based on a GIS for environmental management: A case study in Xingguo county of China. Journal in Ecological Indicators, 51, 3-12. https://doi.org/10.1016/j.ecolind.2014.08.042
- Yun, S., Shal, G., Wenbao, M. and Wei, S. (2015). Analysis of the Ecological Sensitivity of Pengyang County based on Key Factors. The Open Biotechnology Journal, 9, 21-26. https://doi.org/10.2174/1874070701509010021
How to cite this article
APA
Kontos, T., & Katikas, L. (2019). Delimiting Future Urban Sprawl Boundaries Using a GIS-based Model for Ecological Sensitivity Index Assessment and Optimization Techniques. The Case of Mytilene (Lesvos Island, Greece). European Journal of Sustainable Development Research, 3(1), em0074. https://doi.org/10.20897/ejosdr/3975
Vancouver
Kontos T, Katikas L. Delimiting Future Urban Sprawl Boundaries Using a GIS-based Model for Ecological Sensitivity Index Assessment and Optimization Techniques. The Case of Mytilene (Lesvos Island, Greece). EUR J SUSTAIN DEV RES. 2019;3(1):em0074. https://doi.org/10.20897/ejosdr/3975
AMA
Kontos T, Katikas L. Delimiting Future Urban Sprawl Boundaries Using a GIS-based Model for Ecological Sensitivity Index Assessment and Optimization Techniques. The Case of Mytilene (Lesvos Island, Greece). EUR J SUSTAIN DEV RES. 2019;3(1), em0074. https://doi.org/10.20897/ejosdr/3975
Chicago
Kontos, Themistoklis, and Loukas Katikas. "Delimiting Future Urban Sprawl Boundaries Using a GIS-based Model for Ecological Sensitivity Index Assessment and Optimization Techniques. The Case of Mytilene (Lesvos Island, Greece)". European Journal of Sustainable Development Research 2019 3 no. 1 (2019): em0074. https://doi.org/10.20897/ejosdr/3975
Harvard
Kontos, T., and Katikas, L. (2019). Delimiting Future Urban Sprawl Boundaries Using a GIS-based Model for Ecological Sensitivity Index Assessment and Optimization Techniques. The Case of Mytilene (Lesvos Island, Greece). European Journal of Sustainable Development Research, 3(1), em0074. https://doi.org/10.20897/ejosdr/3975
MLA
Kontos, Themistoklis et al. "Delimiting Future Urban Sprawl Boundaries Using a GIS-based Model for Ecological Sensitivity Index Assessment and Optimization Techniques. The Case of Mytilene (Lesvos Island, Greece)". European Journal of Sustainable Development Research, vol. 3, no. 1, 2019, em0074. https://doi.org/10.20897/ejosdr/3975

 Full Text (PDF)
Full Text (PDF)