INTRODUCTION

It is estimated that the buildings’ share of total energy consumption is about 40% (UNEP, 2016). The buildings sector is increasing and this consequently increases energy consumption. Because of this, a reduction of energy consumption and the use of energy from renewable sources represent important steps towards the reduction of greenhouse gas emissions. Measures to reduce energy consumption could be the increased with the use of energy from renewable energy sources respecting the Kyoto Protocol and by ensuring the global temperature rise remains below 2 °C. European parliament agreed that by 2020, the total greenhouse gases emissions must be at least 20% lower and meet the requirements of the EPBD 2010/31/EU (European Parliament, 2010). Reduced energy consumption and increased use of energy from renewable energy sources play an important role in promoting security of energy supply.

One of the promising alternatives for heating is solar energy. Solar energy as an energy source is intermittent so the integration of the thermal energy storage (TES) into a heating system unit is important. The storage ensures more efficient usage of the collected solar energy, as it stores the surplus heat which is not used immediately. In this way, it could be used afterwards, especially if the heating device fails (Stritih and Butala, 2004). An interchangeable operation of the storage (reduced energy consumption) combined with the renewable energy concept, such as combustion of biomass can optimize the performance with regard to decreasing the carbon footprint. The performance of the heat storage device can then be further optimized. For example the alcohol used as a working medium in thermo syphon could also produced very good results (Lin et al., 2003).

Heat pump and solar thermal system combinations have been the subject of many theoretical and experimental investigations based on the idea that the purchased energy savings by the combined system will be greater. During winter, the energy that could be collected by the solar system, but which would be too low in temperature to be useful for direct heating, may be used as a source for the heat pump. Since the solar collection system can supply energy at temperatures higher than the ambient outdoor air, the capacity and COP of the heat pump would be greater than that of the conventional type air-source heat pump alone (Harrison, 2017). Bakirci and Yuksel (2011) performed an experimental study to determine the performance of a heat-pump system with solar collectors and a sensible energy storage tank. They demonstrated that the system could be applied for residential heating in the province of Erzurum which experiences the coldest climate in Turkey. Badescu (2003) proposed sizing principles for sensible heat storage device, which is integrated into the heating system. Two modes of the heating system were presented. The first one when heating system was required (TES was getting emptied and possibly also charged) and the other one when it was not (TES was charged). The results showed that the smaller heat storage devices cool faster than larger ones and that the thermal energy stored per month and monthly energy used to drive the heat pump compressor increases in correlation with the length of the tank. Larger units provided heat during longer time periods, even if the heat flux they supply is generally smaller. Badescu (2002) also studied first and second law analysis of a solar assisted heat pump (SAHP) system and found that most of the exergy losses occur during compression and condensation. He reported that the photovoltaic array can provide all the energy required to drive the heat pump compressor. Kaygusuz and Ayhan (1993) studied a SAHP system experimentally and analysed the data using an exergy concept method. Reyes et al. (1998) studied exergy analysis and the optimization of a SAHP system, and discussed the optimum evaporation temperature. Ozgener and Hepbasli (2007) have comprehensively reviewed energy and exergy analysis of SAHP systems. Dikici and Akbulut (2008) studied the performance parameters of the SAHP system and analysed the energy, exergy and second law efficiency of each component. Based on the analysis they showed that when the evaporator exergy loss decreased, the COP increased. Since exergy is the optimal use of energy, the exergy analysis is a useful method to establish the design for the operation of all energy resources.

Apart from sensible heat storage tanks, there is a variety of different media used for filling heat storages devices. One possible medium for heat storing is substances that change the physical state (Phase Change Materials – PCM). They can be used in different systems for both heating and cooling (Osterman et al., 2012; Stritih et al., 2013). They are very successful in reducing the energy requirements of buildings, so latent heat storage is becoming increasingly important (Tyagi and Buddhi, 2007). By using the proper PCM and its proper installation, latent heat storage devices can be economically efficient in the heating and cooling of buildings. PCM solar tank is able to store the energy in a little space and has a higher heat capacity than the conventional tanks (Bhale et al., 2015). Energy storage can be carried out according to the melting/solidification characteristics of PCM. PCM can be in the following form: solid–solid, solid–liquid, solid–gas, liquid–gas and vice versa. Solid–liquid transitions have proved to be economically attractive for use in TES systems because they have a higher latent heat of phase transition than solid-solid transformation and involve a smaller change in volume than solid-gas or liquid-gas. The choice of the substances used largely depends on the temperature level of the application. The right melting point enables a full phase change potential over the selected time cycle. Thereby, the latent heat can be fully utilized. PCMs in solar heating/cooling plants perform better than sensible heat storage during periods when the mean temperature of the storage is around the melting temperature of the selected PCM (Sharma et al., 2009).

Despite the advantages of PCMs (high storage density, small temperature variation from storage to retrieval and low melting temperature), low thermal conductivity is the major drawback which leads a decrease in the rates of heat storage and limiting their utility areas and widespread use (Osterman et al., 2012). For mass use, it is necessary to solve some problems of reliability and practicality (Zhang et al., 2006). Above all, attention must be paid to thermal characteristics of PCM (Kenisarin and Mahkamov, 2007). Over the past twenty years, PCM and energy storage has been an important subject of research. Review of publications on TES using a solid-liquid phase change was made by Zalba and other authors (2003). For the base three different types of paraffin each with different melting temperatures were taken. The impact of the Reynolds and Stefan number on melting and solidification of PCM was determined (Akgun et al., 2008). In analysing the behaviour of PCM - paraffin in capsules, it was found that the phase change occurs in the temperature interval. Use of the enthalpy method showed that the melting process depends mainly on the size of the Stefan’s number, the temperature at which phase change occurs, and the diameters of capsules (Regin et al., 2006). A wide range of investigations were carried out to enhance the thermal conductivity of the organic PCMs (Paksoy and Sahana, 2012; Aguila et al., 2018; Atinafu et al., 2018). One of the enhancing techniques is dispersing carbon nanotubes (CNTs) with extremely high thermal conductivity to form composite PCMs (Wang et al., 2010). Another technique to enhance thermal conductivity of PCMs are carbon fibers with high thermal conductivity. Carbon fibers are strongly resistant to corrosion and chemical attack. Thus, they are supposed to be compatible with most PCMs (Fukai et al., 2000). Some of the other possibilities are the microencapsulating technique and the placing of metal structures in the PCM (e.g. fins to distribute heat) (Lin et al., 2018). The mathematical modeling of a PCM passive LHTES (latent heat thermal energy storage system) can be used for the optimum material selection and to assist in the optimal designing of the system (Pop et al., 2017). The difficulty in numerically solving a phase-change problem is the solid-liquid interface boundary, known as the Stefan problem. Several authors solved the Stefan problem, Dutil et al. (2011) are one of them. Mazzeo and Oliveti (2017) performed the parametric study and Mazzeo et al. (2017) also the validation of the exact analytical solution.

Latent heat storage devices can be used in heating systems together with solar collectors and heat pumps. A simulation was performed for the system with a latent heat storage device with measurements of inlet and outlet temperatures of the latent heat storage device filled with PCM (Esen, 2000; Lu et al., 2018; Strtih et al., 2018). In such a system, some design factors are important for the performance of the system (Comakli et al., 1996). An example of a design factor could be fins on the heat storage device. A comparison was made between a flat heat storage device and a heat storage device with fins. It turned out that in the heat storage with fins PCM melting time was reduced (Stritih, 2004).

In the last ten years, much interest was attracted by sorption and thermochemical heat storage devices (Ristić et al., 2012a; Ristić et al., 2012b; Krese et al., 2018). In this area, some projects concerning absorption and adsorption heat storage devices are carried out. Their use is limited due to the high cost of materials. The advantage of this technology is the possibility of long-term heat storage (N’Tsoukpoe et al., 2009).

In general, the building application of latent heat storages (LHS) for heating and cooling systems is still at its innocence (Lizana et al., 2018). Based on the researches performed on topic of the LHS combined with solar thermal systems, the systems have a high potential for the use in building sector. The commercialisation of the LHS is low, because the PCM present 75% of the entire system’s costs. However, according to International Energy Agency, their economic feasibility should be increased by 2030.

In 2017, a European project funded by Horizon 2020 named HEART (Holistic Energy and Architectural Retrofit Toolkit) was launched (HEART, 2017). One of the project’s tasks is to improve the buildings’ energy efficiency (retrofit) by renovating the building with a combination of built-in photovoltaics (BIPV), thermal heat storage, heat pumps and air-convectors with local heat pumps installed. The renovation approach and systems components in project HEART are conceptually similar to the components presented in this study.

The aim of this study is to determine the energy performance and the carbon footprint of a system using a solar collector (primary thermal energy source), latent heat storage, heat pump, biomass boiler (secondary thermal energy source) and heat storage for the heating of a building in 4 different climate types (Ljubljana, Adana, Rome and Stockholm).

Firstly, the paper gives the detailed description of the system. Afterwards, the calculation model calculated by the MSOffice Excel is provided. The results show the system’s energy and environmental performance. The accuracy of the results depends on the accuracy of the model itself, which in turn depends on the accuracy of each component.

Since the system is meant for heating, the results are presented for the heating season. The results show the solar gains, heat losses, heat produced by the heat pump, Coefficients of Performance (COP), the biomass heat loads, the annual CO₂ emissions, and CO₂ emissions savings %S that can be achieved with the proposed SAHP system compared to conventional heating systems emissions.

The goal and the novelty of this study is the estimation of the energy savings of the above presented system that can be obtained by using renewable energy sources. Also, the study shows the CO₂ footprint reduction based on the heating systems.

DESCRIPTION OF THE SYSTEM

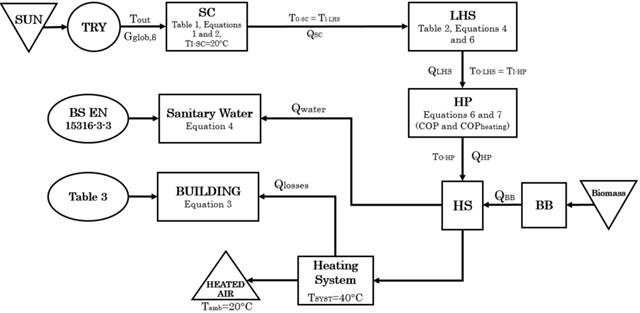
Solar energy is absorbed by the solar collector onto water media and then transmitted by the heat exchanger to the latent heat storage device filled with a phase changing material (PCM) - paraffin. The energy is stored in the PCM in the process of changing its physical state from solid to liquid. Thermal energy is then used by the heat pump from the latent heat storage device to a higher temperature level. Further, the energy is stored in a sensible heat storage device and then sent through a heat exchanger into the heating system which is used for heating the building and for the preparation of sanitary water.

This system is presented in Figure 1.

The system is water based which means that the media running in it and transferring the thermal energy (heat) is mainly water, except the heat pump, which uses a refrigerant (R-407c a mixture of hydrofluorocarbons) for its media.

 

Figure 1. Scheme of the heating system

 

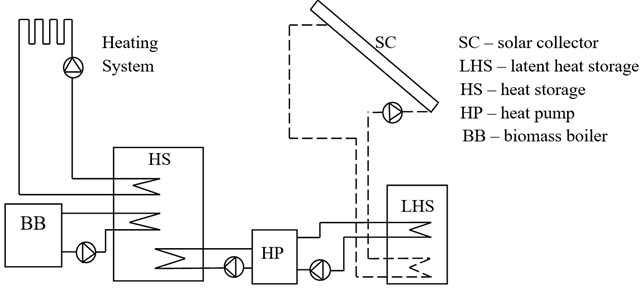
Solar Energy Collector

Solar radiation is a sustainable source of energy. The annual amount of solar energy that falls on Earth is more than eight thousand times larger than the annual global demand for primary energy (Domanski, 2003). Local distribution of the total annual amount of solar energy is determined by climatic and meteorological factors that are highly dependent on their location.

Therefore, the solar energy collector absorbing solar energy on water media was used. The heated water is then transmitted by the heat exchanger and then further to the Latent heat storage (LHS).

The solar energy collector is designed to convert solar energy into heat. In the analysed system two solar collector units of type GreenLAND were used (GreenLAND Systems, 2018). The solar collector consists of a vacuum tube enhancing the absorption of the water (absorber). The characteristics of a single unit are presented in Table 1. The solar collector has an area of 25 m² which was chosen based on former knowledge. The rest of the data corresponds with the referenced example of type GreenLAND.

 

Table 1. Characteristics of the solar collector and absorber F' ASC [m2] Gglobal,β [W/m2] τcover αabs USC [W/m2K] Tmean [K] TI-SC [°C] \(\dot{\mathbf{m}}\)[kg/s] 0.95 25 500 1 0.95 1.5 30 20 0.083

 

Latent Heat Storage (LHS) with Paraffin Rubitherm RT 31

Secondly, the water runs to the latent heat storage device filled with a phase changing material (PCM) - paraffin through the heat exchanger. The PCM then stores the energy in the process of changing their physical state from solid to liquid. In this case, the melting temperature was 31 °C, suitable for energy storage at low temperature level (RUBITHERM GmbH, 2013). This type of PCM material was chosen based on the performing temperature range of the LHS. The inlet temperature of the LHS is similar to the outlet temperature from the solar collector, in the range of 20 - 40 °C (since the heating system demand is 40°C). The Differential Scanning Calorimetry (DCS) thermogram of paraffin is shown in Figure 2.

 

Figure 2. DCS thermogram of paraffin Rubitherm RT31 (Rubitherm GmbH, 2013)

 

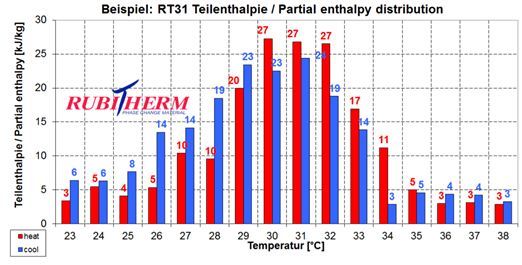
The main advantages of the RT 31 paraffin are high TES capacity, constant temperatures of the heat storage and heat release, chemically inert and without the super cooling effect (Knut, 2016). The material has a stable performance through the cycles of the phase change (long life). The rest of the characteristics of the heat storage are given in Table 2.

 

Table 2. The characteristics of the PCM paraffin RT 31 (Greenland, 2018) Cp,s [kJ/kgK] Cp,l [kJ/kgK] ρs [kg/m3] ρl [kg/m3] Tmp [°C] qs [kJ/m2] 1.8 2.4 880 760 31 150

 

Heat Pump (HP)

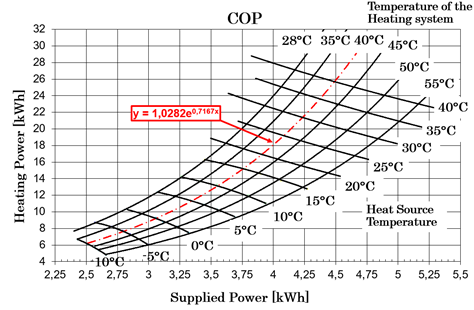
The heat pump transfers the thermal energy from the latent heat storage to the Heat Storage (HS). The role of heat pump in the heating system is to raise the thermal energy from a lower temperature level to a higher temperature level. The coefficient of performance (COP) for the chosen heat pump has been determined, as described in Section 3 of this article.

As a part of model preparation two different types of COP were determined. The first COP (abbreviation: COP) refers to the heat pump’s performance with regard to the power (electricity) used for the pump’s function in relation to the pump’s heating power. The second COP (abbreviation: COP_heating) treats the power that the heat pump produces for the system in relation to the power the heating system needs to provide the required ambient temperature.

The chosen model and COP chart was obtained from the heat pump (Knut, 2016). Its characteristic are shown in the graph below (Figure 3). The vertical axis shows Heating power and the horizontal axis the Supplied power, both in kWh. The relationship shows the Temperature of the Heating System and the Heat Source Temperature. The Temperature of the Heating System (T_syst) was 40 °C.

 

Figure 3. Diagram for determination of COP (Knut, 2016)

 

Heat Storage (HS) and Heating System

The energy is stored in HS and then sent through a heat exchanger into the heating system which is used for heating of building. In this way an ambient air temperature of 20 °C can be provided. The temperature of the heating system is 40 °C, which is estimated to deliver the sufficient indoor environment conditions (ambient temperature). The HS volume was determined to be 3 m³. This is a model simplification. The improved version could have a component of a control system taking into account the variables (internal gains etc.) in the building’s ambient interior.

Biomass Boiler (BB)

When the sun was not able to provide sufficient thermal energy, a secondary heating system, which in our case was a biomass boiler, was switched on and served as a supplementary water heating generator. The BB used in the model is only schematic, and therefore the model treats it as a part of the energy lacking from the latent heat storage to maintain the ambivalent requirements.

Low Energy Building

Finally, the Heating System is established for heating a contemporary residential family building consuming low amounts of energy. The building has high levels of thermal insulation, low levels of air infiltration in its envelope, a sophisticated heat recovery ventilation, energy efficient openings and active solar technologies. Such are typically used in low energy buildings to reduce energy consumption for heating and cooling.

The installed system was used for the heating of a low energy building with the following characteristics shown in Table 3. The values and data were estimated as in input for a low energy building. It is estimated that all spaces of the building are heated as single zone and that there is no ventilation or heat gains. The building model is in this case only an estimation, since the emphasis of the study is in comparison of the final CO₂ equivalents.

 

Table 3. Characteristics of low energy building A [m2] U [W/m2K] Tamb [°C] Tsyst [°C] 300 0.2 20 40

 

The envelope area is estimated for a small residential building. The estimated U-value averages all of the envelope’s surfaces including the openings, as guided in ISO 6946 (ISO, 2007). During the heating season, within the standard ISO 7730 the guideline for an Operative temperature is 22±2 °C (Category B) (ISO, 2005). Air velocities in the residential building are expected to be low and the temperatures of the surrounding surfaces slightly higher, therefore an estimated surrounding air temperature around the heating system is 20 °C. Based on the experiences, the temperature of the heating system was estimated to be 40 °C in order to establish a required ambivalent temperature.

Location

In order to compare the various energy efficiency performances and CO₂ emissions, the bulidng’s performance was studied in 4 different European cities, namely in Ljubljana, Adana, Rome and Stockholm. The data for number of inhabitants was collected (City population, 2018). Four 4 persons per household (building) were assumed. Thus, the number of houses in the city was determined, as shown in Table 4.

 

Table 4. The number of inhabitants and houses for each city studied (City population, 2018) City Inhabitants No. of houses in city Adana 2125000 531250 Rome 2645000 661250 Ljubljana 280000 70000 Stockholm 881000 220250

 

CO₂ Emissions

The values for carbon dioxide intensities (g/kWhe) of electricity used by the operation of the heat pump are given in Table 5. They are analyzed for the cities located in Europe and presented by ASHRAE (American Society of Heating, Refrigerating and Air-Conditioning Engineers) (ASHRAE, 2013). Table 6 shows the combustion emission factors for the fuel emmisons of CO₂ obtained from International Energy Agency (IEA) (IEA, 2017).

 

Table 5. CO2 emissions per kWh from ele ctricity generation for different countries (IEA, 2017) Country [g CO2/kWhe] Turkey 489 Italy 423 Slovenia 325 Sweden 22

 

Table 6. Fossil fuel emission [tons CO2/GJ] (ASHRAE, 2013) Fossil fuel Emission [tonsCO2/GJ] Natural gas 0.051 Oil 0.073 Coal 0.0905

 

MATHEMATICAL MODEL

The simplified model for calculation is presented in Figure 4.

 

Figure 4. The simplified model for calculation, Note: The text in italic marks the corresponding forms of energy

 

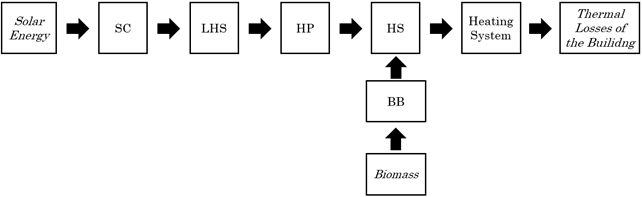
The model was calculated using MSOffice Excel software following the procedure described below. The residential low energy building was chosen as a contemporary example of a family’s home. Based on the needs the required size of the system was estimated as described in Chapter 2.

Firstly, the climatic data for a Test Reference Year (TRY) in Ljubljana, Adana, Rome and Stockholm were collected including the hourly air temperature measured in the shadow and a global solar radiation in the plane of the collector cover (\(G_{\text{global.β}}\)).

Following Equation 1 and values from Table 1, the heat obtained from the solar collector \(Q_{\text{SC}}\) was determined in [W] and then recalculated into [kJ] for each hour of TRY (Medved and Novak, 2000).

\[Q_{\text{SC}} = F^{'} \bullet A_{\text{SC}} \bullet \left\lbrack G_{\text{glob.β}} \bullet \tau_{\text{cover}} \bullet \alpha_{\text{abs}} - U_{\text{SC}} \bullet \left( T_{\text{mid}} - T_{\text{amb}} \right) \right\rbrack\]

(1)

Based on \(Q_{\text{SC}}\) the outlet temperature from the solar collector (\(T_{O - SC}\)) was calculated using Equation 2. If the \(Q_{\text{SC}}\) was a negative value, then the solar collector was switched off. The output temperature of the water in the collector was calculated following Equation 2 and \(T_{I - SC}\) = 20 °C, water heat capacity: \(C_{w}\) = 4200 kJ/kg and \(\dot{m}\) = 0.083 kg/s (EN 15316-4-3:2007, 2007).

\[T_{O - SC} = \frac{Q_{\text{SC}} + \dot{m} \bullet T_{I - SC} + C_{w}}{\dot{m} + C_{w}}\]

(2)

An hourly heat loss from the building’s envelope \(Q_{\text{losses}}\) in [kJ] was calculated using Equation 3 and the values determined in Table 3. EN 13790:2008 describes a method where the heating demand is determined by the transmission, ventilation heat losses and heat gains (EN 13790:2008, 2008). Simplifications are presented in Section 2.6.

\[Q_{\text{losses}}(t) = A \bullet k \bullet (T_{\text{amb}} - T_{\text{out}})\]

(3)

The amount of hot sanitary water demand \(Q_{\text{water}}\) in [kJ] was estimated for an hourly consumption with peaks in the morning and in the evening, according to the BS EN 15316-3-3 (EN 15316-3-3:2007, 2007). The amount of energy consumed for the preparation of the sanitary water was determined based on Equation 4, (valid only for the sensible heat).

\[Q = \dot{m} \bullet c_{p} \bullet \rho \bullet \mathrm{\Delta}T\]

(4)

\(Q\) is the amount of energy needed to heat up the mass (\(m\)) for the temperature gradient (\(\mathrm{\Delta}T\)) with the specific thermal capacity (\(c_{p}\)) and \(\rho\) = 1 at constant air pressure.

The hourly heat in the HS \(Q_{\text{HS}}^{t}\) in [kJ] was determined by following the Equation 5. The change in the energy balance depends on the previous energy level in the storage and the hourly heat changes/deviations of the solar gains \(Q_{\text{SC}}\), the building’s envelope \(Q_{\text{losses}}\) and the sanitary water demand \(Q_{\text{water}}\).

\[Q_{\text{HS}}^{t} = Q_{\text{HS}}^{t - 1} + Q_{\text{SC}} + Q_{\text{losses}} - Q_{\text{water}}\]

(5)

Hourly \(Q_{\text{HS}}\) has to be delivered by the HP and thus, the LHS filled with solar heated PCM. Hourly \(Q_{\text{HS}}\) (demand) was compared to the Rubitherm 31 temperature-enthalpy (Q-T) diagram with specified curve inclinations in Figure 5.

 

Figure 5. The temperature distribution in latent heat storage tank with paraffin RT31

 

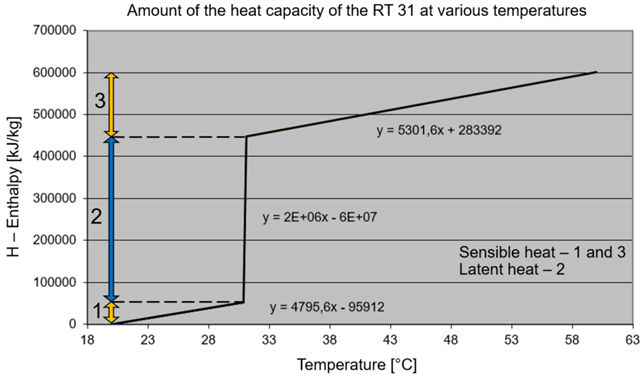
Figure 5 presents the calculated relation of the amount of heat stored in the LHS at various temperatures of the LHS. The formulas written in the graph indicate the inclination of the curve. The heat is added to (or removed from) the material. In the first range, the paraffin (PCM) changes the temperature – the sensible range. In the second range, the material starts melting (or conglobing) as the material changes the phase – the latent range and in the third range it again changes temperature and falls into the sensible range.

The numerical limits of the PCM’s phase change are presented:

• limit 1: Q (T = 30.9 °C) = 52272 kJ (the limit for sensible heat accumulation);

• limit 2: Q (T = 31.1 °C) = 448272 kJ (the limit for latent heat accumulation);

• limit 3: Q (T = 60.0 °C) = 601488 kJ (the absolute theoretical upper value for the model, as the system is not required to deliver temperatures higher than 40 °C into the heating system).

Based on the limit, the PCM phase state is determined and so, the correct correlation for further calculations of the temperature in the LHS. When knowing the range, with the hourly value of Q_HS the corresponding T_LHS can be determined. For temperature determination in the sensible range, see Equation 3 and for the latent range, Equation 6. The model of the LHS is one-dimensional, assuming the temperature of the PCM within the phase change is constant and uniform along the entire storage. Similar model was proposed by (Fortunato et al., 2012).

The phase change of the material appears at constant air pressure. The amount of heat needed to melt the mass (m) is shown in Equation 6, where q_t stands for the specific latent heat for melting the substance. The equation is valid for the 2^nd) - latent phase (phase change is in progress) (Figure 5).

\[Q = m \bullet q_{t}\]

(6)

Knowing the heating system operational temperature (40 °C) and the COP correlation curve y = 1.0282e^0.7167x for the chosen commercial model of the heat pump and T_LHS (the outlet temperature from the supply temperature in), the supply and heating power of the HP are determined (BS EN 15316-4-2:2008, 2008).

The COP [/] of the HP is calculated following the Equation 7. (\(Q_{C}\) - heat from a heat source and \(W_{\text{HP}}\) – energy supplied from the heat pump).

\[COP\ = Q_{C}/W_{\text{HP}}\]

(7)

The COP was chosen to be in the range from 4 to 5 or the HP (with SC and LHS) was switched off (not used). This is when the T_O-LHS or T_I-HP was outside of 15 - 35 °C.

When the HP was switched off, the BB was switched on to deliver the heat demanded. The demanded energy for heating with HP was determined by multiplying the COP with the heat required. The COP for the heating fulfilled with the HP is determined with Equation 8 (BS EN 15316-4-2:2008, 2008).

\[\text{COP}_{\text{heating system}} = \frac{Q_{\text{SAHP}} + W_{\text{HP}}}{W_{\text{HP}}}\]

(8)

At the end the energy data was summarized for every month and the whole season. The values were calculated for the solar gains – heat generated by the sun \(Q_{\text{SC}}\), the heat lost from the building \(Q_{\text{losses}}\), the electricity used for the heat pump’s operation expressed in COP and the electricity used for heating the entire building wheh the HP was working in \(\text{CO}P_{\text{heating}}\) and finally, the amount of the energy left for heating the building with the biomass \(Q_{BB/HS}\).

The schematic approach of the Energy Performance calculation model is presented in Figure 6.

 

Figure 6. The schematic approach of Energy Performance model

 

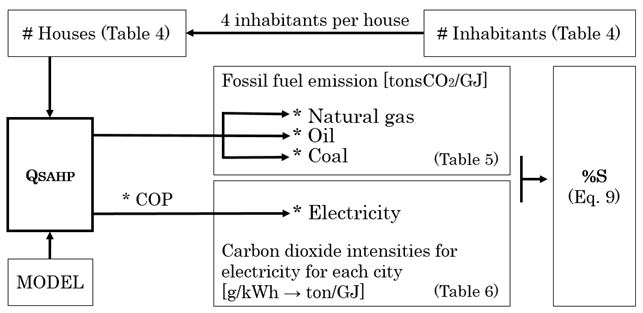
The number of inhabitants (City population, 2018) divided by 4 members per house detrmines the number of houses in every city. It is important to stress out that the results presented do not involve the part of the energy used for heting with the biomass, since theoretically the rest of the heating systems could also be coupled with BB and in this way present similar results. So, the enregy is produced only for SAHP (\(Q_{\text{SAHP}}\)). The energy used for HP operation is later on multiplied with corresponding hourly COPs and summerized.

The CO₂ emission model was prepared based on the energy efficiency model. Formerly determined losses for one house were used to find the yearly emissions of CO₂ for gas, coal, oil per city. The schematic approach of the CO₂ emissions model is given in Figure 7.

 

Figure 7. The schematic approach of the CO2 emissions model

 

CO₂ emissions savings (%S) that can be achieved with the proposed SAHP system is calculated from Equation 9. For reheating by biomass, CO₂ emissions are taken as zero.

\[\% S = \ \frac{E_{F}{- E}_{\text{SAHP}}}{E_{F}} \times 100\]

(9)

Overall, the study could be upgraded to more holistic approach with combination of different types of software equipement – such as, Energy Plus, Trnsys and LCA software.

RESULTS AND DISCUSSION

An analysis of a complex heating system has been conducted for a period of heating season, which we define as the period between October and March. Data on climatic conditions have been obtained for the cities: Adana, Rome, Ljubljana and Stockholm.

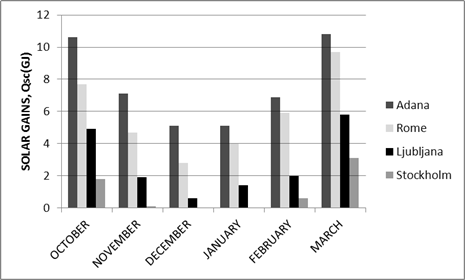
The solar gains of the cities are obtained for the months of the heating season (Figure 8). The analysis showed that the maximum solar gains through the entire heating season are highest in Adana where in March the solar gains reached 10,8 GJ. In Stockholm maximum solar gains were likewise reached in March (3.1 GJ) but the value is unparalleled with solar gains in Adana and Rome. During the months of December and January, solar gains in Stockholm are almost zero (having only reached 0,03 GJ).

 

Figure 8. Solar gains during the heating season

 

Heat losses in the heating season are the largest in Stockholm (6.2 GJ) and the smallest in Adana (1.8 GJ). For all of the cities, maximal losses are in January (Figure 9). From Figure 9 and Figure 10 the trend can be seen – geographical location of each city determines the solar gains and heat loss of a building. Buildings in southern cities have less heat loss and obtain more solar gains and vice versa.

 

Figure 9. Heat losses during the heating season

 

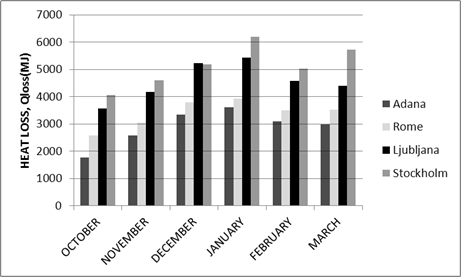
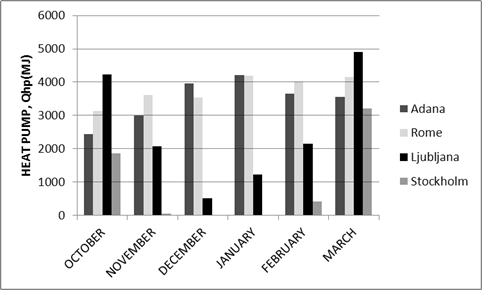
Figure 10 presents data of the heat obtained with a heat pump by month during the heating season. From the diagram, we can see that it is possible to get more heat in March. This fact is linked to a sufficient amount of sun energy during this month. On average, the maximum possible gain of heat from a heat pump is in Adana (maximum 4.2 GJ in January) and in Rome (maximum 4.2 GJ in January). Maximum heat gain can be achieved in Ljubljana in March, where heat from the heat pump reached 4.9 GJ, while the lowest results are in Stockholm in November (0.044 GJ). It can also be seen that in Stockholm during the month of December and January, temperatures and solar gains are not appropriate and the heat pump cannot operate.

 

Figure 10. Heating with solar assisted heat pump in the heating season

 

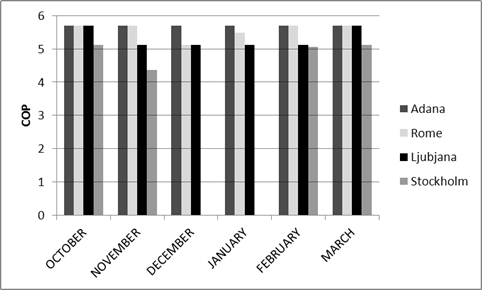
Efficiency of the heat pump or coefficient of performance (COP) gives us the ratio between produced heat and input energy (electricity). In the presented system, COP reached values between 0 and 5.69 during the heating season. A Value of 0 means that there was no (or not enough) solar energy. As presented in Figure 11, a value of 0 was reached in Stockholm in December and January. The maximum value of COP 5.7 was reached in Adana, Rome and Ljubljana. In Adana, COP 5.7 was present during the entire heating season. In Rome, this value was attained in the months of October, November, February and March and in Ljubljana during October and March, while in Stockholm, the maximum value of COP was 5.12.

 

Figure 11. Maximum COP values during the heating season

 

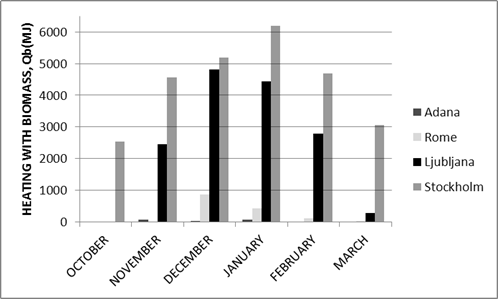
In some climates, there may not be enough solar energy for heating with a heat pump during the entire heating season, so as a consequence reheating is needed. As a back-up, biomass has been chosen. As shown in Figure 12, the greatest need for biomass is in Stockholm during the entire heating season, reaching a maximum in January (nearly 6.2 GJ). In Ljubljana, 4.2 GJ of additional heating with biomass is needed in December. It should be said that reheating is necessary throughout the heating season in all of the discussed cities, but such a need is relatively small in Adana and Rome at 1% and 7%, respectively. In Ljubljana and Stockholm, the share of reheating by biomass system is 54% and 85%, respectively.

 

Figure 12. Additional heating with biomass in the heating season

 

In order to assess the environmental feasibility of SAHP, the CO₂ emissions associated with SAHP operation is compared to conventional heating systems emissions. The overall potential for CO₂ reductions is determined by the emissions of each energy source and the efficiency of energy conversion used to meet heating loads. Natural gas produces emissions of 51 kg CO₂ eq./GJ, while heating oil is associated with emissions of 73 kg CO₂ eq./GJ and coal in the range of 93 – 88 kg CO₂ eq./GJ. The monthly average heating loads for a 300 m² in the cities analyzed in this study are shown in Table 6.

 

Table 6. Monthly average heating loads in GJ for a (300 m2 envelope) building in the cities analyzed in this study Months QSAHP - Heating Load (GJ)   Adana Rome Ljubljana Stockholm October 1.76 2.58 3.57 4.07 November 2.57 3.06 4.18 4.59 December 3.34 3.80 5.23 5.19 January 3.60 3.93 5.44 6.19 February 3.09 3.49 4.57 5.03 March 2.98 3.52 4.40 5.72 TOTAL 17.34 20.38 27.38 30.78

 

The annual CO₂ emissions based on the heating loads given in Table 6 and % S are compared in Table 7 for total building stock in each city.

For Adana and Rome, where SAHP could be operated throughout almost the entire heating season, the CO₂ emissions saving potential is between 53% and 77%. For Ljubljana, the savings are in the order of 66% to 81%. For Stockholm, which uses 85% biomass to meet the heating demand, the savings potential is above 98%. This shows that in climates like Stockholm, where solar energy is scarce in winter, large savings can be achieved with a biomass backup system.

 

Table 7. Comparison of CO2 emissions and % S of SAHP system with reference systems using different fossil fuels for total building stock in each city   SAHP Natural Gas Oil Coal   CO2 (kton/year) CO2 (kton/year) %S CO2 (kton/year) %S CO2 (kton/year) %S Adana 220 469,9 53 672,7 67 833,9 74 Rome 285,9 687,3 58 983,8 71 1219,6 77 Ljubljana 328,1 97,8 66 139,9 77 173,5 81 Stockholm 535,9 345,8 98 495 99 613,6 99

 

CONCLUSIONS

The SAHP system proposed here combines solar energy, a heat pump and a latent heat storage system. As a backup system when solar energy is not sufficient, a biomass system is included for reheating. Energy performance and environmental benefits of the system are calculated for Adana, Rome, Ljubljana and Stockholm with different climate conditions. The results show that the maximum COP values of the SAHP system is more than 5 for all cities. This shows that heat pump performance can be increased significantly in a system assisted with solar energy and latent heat storage. The SAHP system can be used throughout almost the entire heating season for Adana and Rome, which have abundant solar energy. For Ljubljana and Stockholm, a backup system is required to meet the heating demand of 54% and 85%, respectively. CO₂ emissions savings in Adana and Rome are in the range of 53% to 77%, depending on the fossil fuel used in the reference system. For Ljubljana and Stockholm, the CO₂ savings are also high, reaching 99% in Stockholm, but the majority of the savings are due to the biomass back-up system. The proposed SAHP system can further be improved by using photovoltaic panels to provide electricity to the heat pump for a zero fossil fuel operation.

Nomenclatures

A	building envelope area (m2)
ASC	solar energy collector area (m2)
cp	Specific heat of the material (J kg-1 K-1)
cp,s	specific heat of PCM in solid phase (J kg-1 K-1)
cp,l	specific heat of PCM in liquid phase (J kg-1 K-1)
cw	specific heat of the water (J kg-1 K-1)
COP	coefficient of performance (-)
COPheating	coefficient of performance for heating (-)
EF	CO2 emissions by fossil fuel reference system (ton)
ESAHP	CO2 emissions by SAHP system (ton)
F'	efficiency factor of the absorber (-)
Gglobal,β	global solar radiation in the plane of the collector cover (W m-2)
H	specific enthalpy (kJ/kg)
\[\dot{m}\]	mass flow rate (kg s-1)
QC	heat from a heat source (kJ)
Qlosses	heat losses through the building’s envelope (kJ)
Qwater	heat demand for sanitary hot water (kJ)
QSC	heat from the sollar collector (kJ)
QLHS	heat from the LHS (kJ)
\[Q_{\text{LH}}^{t}\]	heat from the LHS in hour of the TRY file t (kWh)
\[Q_{\text{LH}}^{t - 1}\]	heat from the LHS in hour of the TRY file t-1 (kWh)
qt	specific latent heat for melting the substance (J kg-1)
qs	specific sensitive heat for melting the substance (J kg-1)
%S	CO2 savings of SAHP system with reference to fossil fuel system (%)
S	specific entropy (J K−1)
Tamb	ambient temperature (°C)
Tmid	mean temperature of the liquid in the collector (°C)
Tmp	melting temperature of PCM (°C)
Tout	the tempearture ouside the building – from the climate file
TI-SC	the inlet temparture of the sollar collector (SC) (°C)
TO-SC	the outlet temparture of the sollar collector(SC) (°C)
TI-LHS	the inlet temparture of the latent heat storage (LHS) (°C)
TO-LHS	the outlet temparture of the sollar collector (LHS) (°C)
Tsyst	the temperature of the heating system (°C)
U	overall thermal transmittance of building (W m-2 K-1)
WHP	heat pump supplied energy (kWh)
Greek letters
αabs	absorptivity of solar radiation on the absorber
ρs	PCM density in solid phase (kg m3)
ρl	PCM density in liquid phase (kg m3)
τcover	transmissivity of the solar energy collector cover

Abbreviations

BB	biomass boiler
HP	heat pump
HS	heat storage
LHTES	latent heat thermal energy storage system
PCM	phase change material
TES	thermal energy storage
SAHP	solar assisted heat pump