Abstract
Active photovoltaic-thermal (PV-T) systems for solar heating and electricity generation are likely to employ the same differential temperature pump controllers as equivalent non-hybrid solar thermal (ST) systems. However, the typical controller setpoint selection methods for cost-effective and stable pump operation fail to consider the effect on photovoltaic (PV) electricity generation taking place in PV-T systems. Analytical relations for the same goals were derived to anticipate this influence using the steady-state Florschuetz PV-T collector model and compared with equivalent numerical methods relying on an extension of the Perers model designed to encompass PV-T collectors, namely by modelling electricity generation and the associated thermal performance reduction. Both methods indicate the minimum turn-on and turn-off setpoints for cost-effective and stable operation increase and decrease, respectively, relative to those for non-hybrid operation of PV-T systems or equivalent non-hybrid systems, and more so at higher irradiance levels, though the variations are shown not to be significant for a range of PV-T systems represented and can be reasoned to be inflated or of limited practical relevance. In conclusion, the effect of pump operation on electricity generation is not predicted to be a determining factor for differential temperature controller setpoint selection in PV-T systems.
Keywords
License
This is an open access article distributed under the Creative Commons Attribution License which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Article Type: Research Article
EUR J SUSTAIN DEV RES, Volume 3, Issue 1, 2019, Article No: em0066
https://doi.org/10.20897/ejosdr/3926
Publication date: 06 Feb 2019
Online publication date: 07 Oct 2018
Article Views: 3569
Article Downloads: 2663
Open Access HTML Content References How to cite this articleHTML Content
INTRODUCTION
Differential temperature control is the standard form of pump control for active low-temperature solar thermal (ST) systems, including photovoltaic-thermal (PV-T) systems (Kalogirou, 2009). While alternative and more complex differential temperature control variants have been proposed, the most common ones are the on/off and proportional variants with static setpoints (Winn, 1993; Kicsiny, 2012; Araújo and Pereira, 2016, 2017; Badescu, 2017). The configuration of these controllers requires at least two setpoints, the turn-on (ΔTon) and turn-off (ΔToff) setpoints, whose selection can be aided by methods originally intended for non-hybrid ST systems. PV-T systems, however, differ from non-hybrid ST systems due to the additional photovoltaic (PV) conversion process, whose temperature dependence means it is also affected by fluid circulation or lack thereof, and consequently by the choice of controller setpoints (Skoplaki and Palyvos, 2009). Hence, setpoint selection for PV-T systems should ideally reflect both their thermal and electrical performances. The efforts described here concern a study on differential temperature controller setpoint selection for PV-T systems, a subject which has eluded discussion in the literature so far, and which can be understood to fall under the scope of the recent IEA-SHC Task 60 on PV-T technology (IEA-SHC, n.d.).
Previous research efforts have largely determined how and to what extent controller setpoints can be expected to influence the thermal energy collection process of non-hybrid ST systems. In essence, higher ΔTon and ΔToff setpoints tend to reduce pump use by causing fluid circulation to start later and stop earlier, respectively, than they would otherwise, which tends to negatively influence the thermal energy collected although not necessarily in a monotonic way, while small deadbands (ΔTon - ΔToff) tend to exacerbate pump cycling (Schiller et al., 1980; Winn, 1983; Hirsch, 1985; Kahwaji and Winn, 1986; Muralidhar et al., 1989). Magnitude-wise, modest ΔTon setpoint increases (5-10 K) relative to low initial setpoints (2-5 K) have been estimated to decrease the daily thermal energy collection efficiency by as much as 26% (absolute), though most severely for low yield days, while shortening pump running times by 3-69% (relative) (Schiller et al., 1980; Kahwaji and Winn; 1986; Huang, 1994). In turn, Hirsch (1985) argued the thermal performance sensitivity to ΔToff was low for typical setpoints around 1 K while Muralidhar et al. (1989) summarised experiments suggesting a higher sensitivity to ΔToff than to ΔTon. Conversely, Winn (1983) analytically determined the pump cycling sensitivity to ΔToff can be as high as 60 cycle/K, for ΔToff = 1 K and ΔTon≈ ΔToff, and as low as 5 cycle/K, for ΔTon≈10 K. These studies ultimately highlight the basic trade-offs implicit with setpoint selection and also inform the most disseminated setpoint selection methods for differential temperature controls.
The setpoint selection methods surveyed were originally intended for non-hybrid ST systems. The standard analytical method relies on the Hottel-Whillier-Bliss (HWB) steady-state model to derive the conditions for cost-effective and stable operation of non-hybrid ST systems or, in theory, of PV-T systems not generating electricity. When combined with the effectiveness-NTU method to encompass both direct (\(\epsilon = 1\)) and indirect (\(\epsilon < 1\)) systems, the generic conditions for cost-effective and stable operation in the presence of measurement errors (\(\varepsilon\)) are given by Eqs. (1) and (2), respectively, where \(A_{c}\) is the collector area, \({F_{R}}^{'}\) is the collector heat exchanger factor, \(U_{L}\) is the overall heat loss coefficient, \(K_{\text{par},\text{aux}}\) is the parasitic to auxiliary energy price ratio, \(P_{\text{el},\text{pump}}\) is the parasitic power required by the pump(s), \(\eta_{\text{th},\text{pump}}\) is the (combined) thermal efficiency of the pump(s) in relation to fluid heating, \((\dot{m}C_{p})_{\min}\) is the lowest of the collector and tank loops’ capacitance rates, and \(\epsilon\) is the heat exchanger (HE) effectiveness (Alcone and Herman, 1981; Beckman et al., 1994).
| \[\Delta T_{\text{off}} > \frac{K_{\text{par},\text{aux}} - \eta_{\text{th},\text{pump}}}{\epsilon(\dot{m}C_{p})_{\min}}P_{\text{el},\text{pump}} + \varepsilon\] | (1) |
| \[\Delta T_{\text{on}} > \frac{\epsilon(\dot{m}C_{p})_{\min}}{A_{c}{F_{R}}^{'}U_{L}}(\Delta T_{\text{off}} - \varepsilon) + \varepsilon\] | (2) |
These design rules can provide useful information for the purposes of setpoint selection. Equation (1) provides sound estimates for the minimum \(\Delta T_{\text{off}}\) setpoint guaranteeing cost-effective pump operation in the presence of measurement errors, and regardless of whether or not timers are used, and thus has strong practical relevance (Schiller et al., 1980; Kahwaji and Winn, 1986; Winn, 1993; Alcone and Herman, 1981). Conversely, Eq. (2) determines a lower \(\Delta T_{\text{on}}\) limit but in practice it amounts to a less relevant upper limit since: i) some pump cycling is generally tolerated and to a largely unspecified extent due to the absence of objectively determined limits; ii) this limit can be seen as either conservative or unreliable because it does take into account the collector heat capacity and the cold stagnated fluid in the connecting pipes, respectively; iii) timers enable much lower \(\Delta T_{\text{on}}\) setpoints to be used without exacerbating pump cycling (Winn, 1993). Hence, despite some limitations, the analytical design rules can narrow down the range of potential setpoints and more so when combined with empirical methods.
Two empirical methods are commonly referenced to guide the setpoint selection process. The first holds that maintaining a given ratio between \(\Delta T_{\text{on}}\) and \(\Delta T_{\text{off}}\) is a condition for stable operation in active ST systems, whereas the second consists of largely undifferentiated setpoint ranges. Schiller et al. (1979) claim the ratios typically vary from 2 up to 7, whereas Winn (1993) cites ratios between 4 up 6 for \(\Delta T_{\text{off}}\) setpoints between 1 and 2 K, and highest when \(\Delta T_{\text{off}}\) is lowest. In turn, the setpoints reported in the literature fall into the following ranges: 3-15 K, for \(\Delta T_{\text{on}}\); and, 0.2-6 K, for \(\Delta T_{\text{off}}\) (Kalogirou, 2009; Winn, 1993; Beckman et al., 1994; Prapas et al., 1995; Knudsen, 2002; Eicker, 2003; Streicher and Kaltschmitt, 2007; Badescu, 2008). Among these, those for indirect systems are generally higher than for direct systems: 8-15 K, for \(\Delta T_{\text{on}}\), and 3-6 K, for \(\Delta T_{\text{off}}\) (Kalogirou, 2009; Beckman et al., 1994). Conversely, the setpoints selected for the test and simulation of PV-T systems – as documented in the literature – have been consistent with the ranges for non-hybrid systems despite the absence of a formal justification for this: 5-10 K, for \(\Delta T_{\text{on}}\); and 1-4 K, for \(\Delta T_{\text{on}}\) (Rockendorf et al., 1999; Huang et al., 2001; Chow et al., 2009; Dupeyrat et al., 2014; Haurant et al., 2014, 2015).
The endeavour described here thus aims to provide theoretical support for differential temperature controller setpoint selection in PV-T systems by also considering the effect of pump operation on electricity generation. In particular, the conditions for cost-effective and stable operation of active PV-T systems were determined using analytical and numerical methods, and parametric analyses conducted to compare setpoint selection between hybrid and non-hybrid systems of various types (Florschuetz, 1979; Perers, 1993). Finally, the study covers direct and indirect PV-T systems for residential solar water heating and grid-tied electricity generation, such as those of Figure 1, due to their perceived market potential (Zondag et al., 2005).
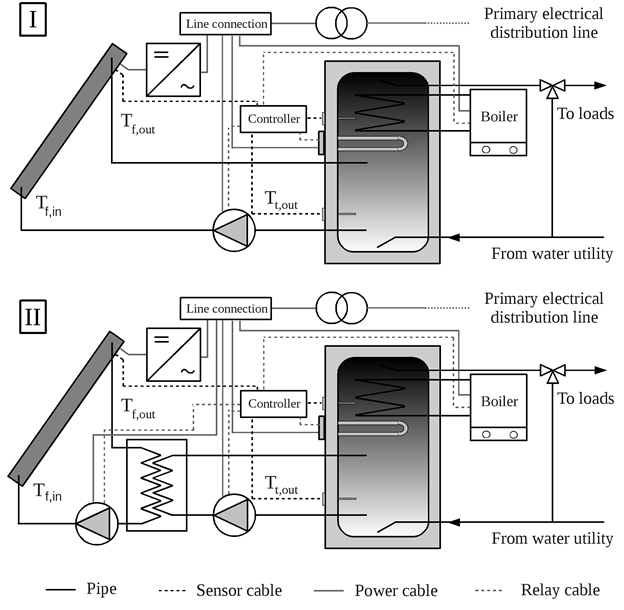
SYSTEM MODELS
The systems represented in this study were reproduced relying on two PV-T collector models, specifically the Florschuetz model and an extension of the Perers model. Both account for the effect of PV electricity generation on the behaviour of PV-T collectors by modelling the cell efficiency as a linear function of the mean cell temperature. The main difference between the models concerns the heat loss coefficient temperature dependence, which is negligible in the Florschuetz model but not necessarily so in the extended Perers model used.
Florschuetz Model
The Florschuetz model extends the HWB model to encompass PV-T collectors and has many similarities with the latter including numerous shared assumptions, such as steady-state operation and a negligible heat loss coefficient temperature dependence, and similar equations and variables (Florschuetz, 1979; de Vries, 1998). When this model is combined with the \(\epsilon\)-NTU method, the useful heat flow rate (\(\dot{Q}\)) and electrical power (\(P_{\text{pv}}\)) generated by direct (\(\epsilon\)=1) or indirect (\(\epsilon\)<1) PV-T systems can be given by Eqs. (3) and (4), respectively, where \(T_{t,\text{out}}\) represents the storage tank fluid temperature near the bottom, \(T_{a}\) is the ambient temperature, \(G_{T}\) is the global irradiance on the collector plane, \(\eta_{\text{pv},r}\) is the cell efficiency at reference conditions (e.g., STC), \(T_{\text{pv},m}\) is the mean cell temperature, \(\beta_{\text{pv}}\) is the MPP cell efficiency temperature dependence, \(\rho_{\text{pv}}\) is the PV packing factor, \(\tau\) is the cover transmittance, and where \(\widetilde{S}\), \({\widetilde{U}}_{L}\) and \({\widetilde{F}}_{R}'\) are PV-T collector equivalents of the solar radiation absorbed at the absorber plate (\(S\)), the overall heat loss coefficient (\(U_{L}\)) and the collector heat exchanger factor (\(F_{R}'\)), respectively, given in Eqs. (5), (6) and (7), which are equal to their non-hybrid counterparts if no electricity is generated (\(\eta_{\text{pv}}\)= 0%). The same can be said of the PV-T collector heat removal factor (\({\widetilde{F}}_{R}\)) and other variables with HWB model counterparts, namely the PV-T collector efficiency factor (\(\widetilde{F}'\)).
| \[\dot{Q} = A_{c}{\widetilde{F}}_{R}'\left\lbrack \widetilde{S} - {\widetilde{U}}_{L}\left( T_{t,\text{out}} - T_{a} \right) \right\rbrack\] | (3) |
| \[P_{\text{pv}} = A_{c}\tau\rho_{\text{pv}}\eta_{\text{pv},r}G_{T}\left\lbrack 1 + \beta_{\text{pv}}\left( T_{\text{pv},m} - T_{\text{pv},r} \right) \right\rbrack\] | (4) |
| \[\widetilde{S} = S\left\lbrack 1 - \frac{\rho_{\text{pv}}}{\alpha}\eta_{\text{pv},r}\left\{ 1 + \beta_{\text{pv}}\left( T_{a} - T_{\text{pv},r} \right) \right\} \right\rbrack\] | (5) |
| \[{\widetilde{U}}_{L} = U_{L} + \tau\beta_{\text{pv}}\rho_{\text{pv}}\eta_{\text{pv},r}G_{T}\] | (6) |
| \[{\widetilde{F}}_{R}' = {\widetilde{F}}_{R}\left\lbrack 1 + \frac{A_{c}{\widetilde{F}}_{R}{\widetilde{U}}_{L}}{{\dot{m}}_{c}C_{p,c}}\left\{ \frac{{\dot{m}}_{c}C_{p,c}}{\epsilon\left( \dot{m}C_{p} \right)_{\min}} - 1 \right\} \right\rbrack^{- 1}\] | (7) |
The electrical efficiency itself is modelled as a linear function of the mean cell temperature, defined in Eq. (8) as a piecewise function of the collector mass flow rate (\({\dot{m}}_{c}\)).
| \[T_{\text{pv},m} = \left\{ \begin{matrix} T_{t,\text{out}} + \left( T_{a} + \widetilde{S}/{\widetilde{U}}_{L} - T_{t,\text{out}} \right)\left( 1 - {\widetilde{F}}_{R}' \right) \\ T_{a} + \widetilde{S}/{\widetilde{U}}_{L} \\ \end{matrix} \right.\ \begin{matrix} ,\ if\ {\dot{m}}_{c} \neq 0 \\ ,\ if\ {\dot{m}}_{c} = 0 \\ \end{matrix}\] | (8) |
Extended Perers Model
The single-node Perers model extension first described in Magalhães et al. (2016) retains many similarities with the Florschuetz model including the electrical efficiency function, but also accounts for a non-negligible heat loss coefficient temperature dependence (\(U_{L,2} \neq 0\)W/m2K2). Though not as relevant, it also assumes a constant PV-T collector efficiency factor (\(\widetilde{F}' = F'\)) and approximates the mean fluid temperature (\(T_{f,m}\)) as the arithmetic mean between the inlet and outlet temperatures (Florschuetz, 1979; Perers, 1993). The resulting steady-state electrical output power is given by Eq. (4), while the steady-state useful heat flow rate is expressed as Eq. (9) and the mean cell temperature as Eq. (10), where \({\widetilde{U}}_{L,1}\) is a function the zero-reduced temperature heat loss coefficient (\(U_{L,1}\)) given in Eq. (11), and analogous to \({\widetilde{U}}_{L}\) in Eq. (6).
| \[\dot{Q} = A_{c}F'\left\lbrack \widetilde{S} - {\widetilde{U}}_{L,1}\left( T_{f,m} - T_{a} \right) - U_{L,2}\left( T_{f,m} - T_{a} \right) \right\rbrack\] | (9) |
| \[T_{\text{pv},m} = T_{a} - \frac{{\widetilde{U}}_{L,1}}{2U_{L,2}} + \frac{1}{2U_{L,2}}\sqrt{{\widetilde{U}}_{L,1} + 4 \cdot U_{L,2} \cdot \left( \widetilde{S} - \frac{\dot{Q}}{A_{c}} \right)}\] | (10) |
| \[{\widetilde{U}}_{L,1} = U_{L,1} + \tau\beta_{\text{pv}}\rho_{\text{pv}}\eta_{\text{pv},r}G_{T}\] | (11) |
For this particular study, the model was further extended to cover PV-T systems with external heat exchangers via the \(\epsilon\)-NTU method in accordance with the system of equations (12) where the collector inlet (\(T_{f,\text{in}}\)) and outlet (\(T_{f,\text{out}}\)) fluid temperatures and \(\dot{Q}\) are dependent variables determined iteratively using the Newton-Raphson method.
| \[\left\{ \begin{matrix} T_{f,\text{in}} - T_{f,\text{out}} + \dot{Q}\left\lbrack {\dot{m}}_{c}C_{p,c} \right\rbrack^{- 1} = 0 \\ T_{t,\text{out}} - T_{f,\text{out}} + \dot{Q}\left\lbrack \epsilon\left( \dot{m}C_{p} \right) \right\rbrack^{- 1} = 0 \\ \end{matrix} \right.\ \] | (12) |
DIFFERENTIAL TEMPERATURE CONTROL SETPOINT SELECTION METHODS FOR PV-T SYSTEMS
The study focused on two differential temperature control setpoint selection methods. The first one is analytical in nature and relies on the Florschuetz model to derive the conditions for cost-effective and stable operation of PV-T systems by replicating the standard approach (Alcone and Herman, 1981; Beckman et al., 1994). The second method does the same, but numerically and using the extended Perers model to encompass a more diverse range of PV-T collectors.
Analytical Method Using the Florschuetz Model
Condition for Cost-Effective Operation
Consider an active low-temperature ST heating system with storage, either direct or indirect with external HE, as shown in Figure 1. The storage tank can be charged via the solar loop or through an auxiliary heater, if and when necessary. However, it is wasteful to leave the supply-loop pump(s) on if the same outcome vis-à-vis useful heat costs less using the auxiliary heater. Hence, a sensible cost-based condition to keep the pump(s) on is given by the inequality (13), where \(p_{\text{el}}\) stands for the general purpose electricity price and \(p_{\text{aux}}\) is the auxiliary energy price.
| \[p_{\text{el}}P_{\text{el},\text{pump}} < p_{\text{aux}}\left( P_{\text{el},\text{pump}}\eta_{\text{th},\text{pump}} + \dot{Q} \right)\] | (13) |
According to this rationale, the pump(s) should be kept on if the condition (13) is met, since it would mean the parasitic costs (\(p_{\text{el}}P_{\text{el},\text{pump}}\)) are lower than the cost of supplying the same heat flow rate (\(P_{\text{el},\text{pump}}\eta_{\text{th},\text{pump}} + \dot{Q}\)) at auxiliary energy prices (\(p_{\text{aux}}\)). For PV-T systems, the PV revenue variation (\(- p_{\text{pv}}\eta_{\text{el},\text{bos}}\Delta P_{\text{pv}}\)) caused by stopping the pump(s) should also be taken into account. Thus, the pump(s) in a PV-T system should remain on as long as the condition (14) is valid, where \(p_{\text{pv}}\) represents the PV electricity price, \(\eta_{\text{el},\text{bos}}\) is the balance-of-system electrical efficiency (assuming independent and flawless maximum power point tracking), and \(\Delta P_{\text{pv}}\) is the bulk PV power gain due to a transition from stagnation to fluid circulation.
| \[p_{\text{el}}P_{\text{el},\text{pump}} - p_{\text{pv}}\eta_{\text{el},\text{bos}}\Delta P_{\text{pv}} < p_{\text{aux}}\left( P_{\text{el},\text{pump}}\eta_{\text{th},\text{pump}} + \dot{Q} \right)\] | (14) |
The bulk PV power gain is given by Eq. (15), according to the Florschuetz model, whereas the PV electricity price can be modelled as Eq. (16), where \(K_{\text{pv},\text{el}}\) represents the relative value of PV electricity generated from a PV-T system in relation to general purpose electricity.
| \[\Delta P_{\text{pv}} = \frac{U_{L} - {\widetilde{U}}_{L}}{{\widetilde{U}}_{L}}\dot{Q}\] | (15) |
| \[p_{\text{pv}} = p_{\text{el}}K_{\text{pv},\text{el}}\] | (16) |
Replacing Eqs. (15) and (16) in the condition (14) and rearranging for \(\dot{Q}\) leads to (17), where \(\Lambda_{\text{pv},\text{off}}\) represents its normalised variation due to the electricity generation, given by Eq. (18).
| \[\Delta T > \frac{\left( K_{\text{par},\text{aux}} - \eta_{\text{th},\text{pump}} \right)P_{\text{el},\text{pump}}}{\epsilon\left( \dot{m}C_{p} \right)_{\min}}\Lambda_{\text{pv},\text{off}}\] | (17) |
| \[\Lambda_{\text{pv},\text{off}} = \frac{{\widetilde{U}}_{L}}{{\widetilde{U}}_{L} + (U_{L} - {\widetilde{U}}_{L})K_{\text{par},\text{aux}}K_{\text{pv},\text{el}}\eta_{\text{el},\text{bos}}}\] | (18) |
The minimum \(\dot{Q}\) expressed through inequality (17) can be converted into a temperature difference requirement (\(\Delta T_{\text{off},min}\)) between the collectors and the tank necessary for useful heat collection, represented as inequality (20), by replacing \(\dot{Q}\) in the inequality (17) with Eq. (19) and rearranging for the temperature difference measured (\(\Delta T = T_{f,\text{out}} - T_{t,\text{out}}\)).
| \[\dot{Q} = \epsilon\left( \dot{m}C_{p} \right)_{\min}\Delta T\] | (19) |
| \[\Delta T > \frac{\left( K_{\text{par},\text{aux}} - \eta_{\text{th},\text{pump}} \right)P_{\text{el},\text{pump}}}{\epsilon\left( \dot{m}C_{p} \right)_{\min}}\Lambda_{\text{pv},\text{off}}\] | (20) |
Condition for Stable Operation
Consider a ST system with stagnated PV-T collectors generating electricity at a uniform and stable temperature (\(T_{c}\)), expressed as Eq. (21) in accordance with the Florschuetz model.
| \[T_{c} = T_{a} + \frac{\widetilde{S}}{{\widetilde{U}}_{L}}\] | (21) |
The temperature difference sensed by the controller immediately before the start of fluid circulation corresponds necessarily to the turn-on setpoint (\(\Delta T_{\text{on}}\)), which is thus given by:
| \[\Delta T_{\text{on}} = T_{a} + \frac{\widetilde{S}}{{\widetilde{U}}_{L}} - T_{t,\text{out}}\] | (22) |
The aforementioned formulation of \(\Delta T_{\text{on}}\) partially resembles the heat flow rate from PV-T collectors, when expressed as Eq. (23), which is obtained by rearranging Eq. (3):
| \[\dot{Q} = A_{c}{\widetilde{F}}_{R}'{\widetilde{U}}_{L}\left\lbrack T_{a} + \frac{\widetilde{S}}{{\widetilde{U}}_{L}} - T_{t,\text{out}} \right\rbrack\] | (23) |
Thus, the \(\dot{Q}\) level attainable through fluid circulation is proportional to the \(\Delta T_{\text{on}}\) setpoint used to trigger it, which must be at least positive for useful thermal energy collection:
| \[\dot{Q} = A_{c}{\widetilde{F}}_{R}'{\widetilde{U}}_{L}\Delta T_{\text{on}}\] | (24) |
On the other hand, stability requires that \(\Delta T_{\text{on}}\) must not only be greater than \(\Delta T_{\text{off}}\) – since fluid circulation stops when \(\Delta T\) reaches \(\Delta T_{\text{off}}\) – but also such that the \(\dot{Q}\) returned by Eq. (24) is superior than the one returned by Eq. (19), for a given \(\Delta T_{\text{off}}\). Otherwise, \(\Delta T\) will drop below \(\Delta T_{\text{off}}\) once fluid circulation begins, causing pump cycling in the process.
| \[A_{c}{\widetilde{F}}_{R}'{\widetilde{U}}_{L}\Delta T_{\text{on}} > \epsilon\left( \dot{m}C_{p} \right)_{\min}\Delta T_{\text{off}}\] | (25) |
Rearranging the inequality (25) for \(\Delta T_{\text{on}}\) yields (26), a simple condition for stable operation of PV-T systems. This condition is sensitive to the PV conversion process through \(\Lambda_{\text{pv},\text{on}}\), given by Eq. (27), which equals one for non-hybrid operation or equivalent non-hybrid systems.
| \[\Delta T_{\text{on}} > \frac{\epsilon\left( \dot{m}C_{p} \right)_{\min}}{A_{c}F_{R}'U_{L}}\Delta T_{\text{off}}\Lambda_{\text{pv},\text{on}}\] | (26) |
| \[\Lambda_{\text{pv},\text{on}} = \frac{F_{R}'U_{L}}{{\widetilde{F}}_{R}'{\widetilde{U}}_{L}}\] | (27) |
Numerical Method Using the Extended Perers Model
Numerical solutions to the conditions for cost-effective and stable operation of PV-T systems were also obtained. This required the above-named conditions to be generalised from their analytical counterparts to form Eqs. (28) and (29), which were iteratively solved by relying on calls to functions derived solely from the extended Perers model, which primarily relies on \(F'\). The functions included the collector temperature during stagnation (\(T_{\text{stag}}\)), \(T_{f,\text{out}}\), \(\Delta P_{\text{pv}}\) and the \(\dot{Q}\).
| \[\Delta T_{\text{off},min} - \frac{K_{\text{par},\text{aux}} - \eta_{\text{th},\text{pump}}}{\epsilon\left( \dot{m}C_{p} \right)_{\min}}P_{\text{el},\text{pump}} + \frac{K_{\text{pv},\text{el}}K_{\text{par},\text{aux}}\eta_{\text{el},\text{bos}}}{\epsilon\left( \dot{m}C_{p} \right)_{\min}}\Delta P_{\text{pv}} = 0\] | (28) |
| \[\left\{ \begin{matrix} \Delta T_{\text{on},min} - T_{\text{stag}} + T_{t,\text{out}} = 0 \\ \dot{Q}/\left\lbrack \epsilon\left( \dot{m}C_{p} \right)_{\min} \right\rbrack - \Delta T_{\text{off}} = 0 \\ \end{matrix} \right.\ \] | (29) |
The condition for cost-effective fluid circulation is translated by Eq. (28), and was solved iteratively by relying on calls to the functions for \(T_{f,\text{out}}\) and \(\Delta P_{\text{pv}}\), both of which functions of \(T_{t,\text{out}}\). Initial estimates were thus necessary and set to the closed-form Florschuetz model solutions.
|
Table 1. Reference PV-T system characteristics
|
The same approach to initial estimate selection was adopted to solve the system of equations (29), reflecting the condition for stable operation, which in turn relied on calls to \(\dot{Q}\) and \(T_{\text{stag}}\) to determine \(\Delta T_{\text{on},min}\) and \(T_{t,\text{out}}\), for a given \(\Delta T_{\text{off}}\) setpoint. Finally, the effect of PV electricity generation on \(\Delta T_{\text{off},min}\) and \(\Delta T_{\text{on},min}\) was determined by solving the equations for PV-T systems under hybrid and non-hybrid operation, and computing Eqs. (30) and (31).
| \[\Lambda_{\text{pv},\text{off}} = \frac{\Delta T_{\text{off},min}(\eta_{\text{pv},r} \neq 0)}{\Delta T_{\text{off},min}(\eta_{\text{pv},r} = 0)}\] | (30) |
| \[\Lambda_{\text{pv},\text{on}} = \frac{\Delta T_{\text{on},min}(\Delta T_{\text{off}};\eta_{\text{pv},r} \neq 0)}{\Delta T_{\text{on},min}(\Delta T_{\text{off}};\eta_{\text{pv},r} = 0)}\] | (31) |
ANALYSIS
The controller setpoint design methods described previously were analysed and compared for use in PV-T systems. The analysis focused on a reference indirect PV-T system, characterised by the parameter values found in Table 1, and some parametric variations. The systems are standard residential grid-connected PV-T systems with glazed PV-T collectors whose PV arrays feature crystalline-silicon cells and whose bulk electricity production is obtained through flawless maximum power point (MPP) operation and fed to the local utility grid at a constant balance-of-system electrical efficiency. The methods can nonetheless be applied to direct PV-T systems by assuming the HE is ideal (\(\epsilon = 1\)). For simplicity, the numerical method adopted the same PV-T collector efficiency factor as the Florschuetz model for each irradiance level (\(G_{T}\)), since \(\widetilde{F}'\) is essentially constant and identical to \(F'\) for good collector designs (Florschuetz, 1979).
Analytical Method Using the Florschuetz Model
Both the minimum \(\Delta T_{\text{off}}\) (\(\Delta T_{\text{off},min}\)) and \(\Delta T_{\text{on}}\) (\(\Delta T_{\text{on},min}\)) setpoints for cost-effective and stable operation of PV-T systems derived according to the Florschuetz model were determined to be sensitive to \(G_{T}\), as shown in Figure 2. In essence, they indicate PV-T systems can operate cost-effectively using lower \(\Delta T_{\text{off}}\) setpoints during PV generation (\(\eta_{\text{pv}} \neq\)0%; \(\Lambda_{\text{pv},\text{off}} <\)1) than under non-hybrid operation (\(\eta_{\text{pv}} =\)0%; \(\Lambda_{\text{pv},\text{off}} =\)1) since keeping the pump(s) running until later while \(\Delta T\) is positive cools the cells and enhances revenue. In turn, higher \(\Delta T_{\text{on}}\) setpoints (for a given \(\Delta T_{\text{off}}\) setpoint) are required to avoid cycling while electricity is being generated (\(\eta_{\text{pv}} \neq\)0%; \(\Lambda_{\text{pv},\text{off}} >\)1) since the reduced effective absorptance caused by PV conversion leads to lower steady-state temperature differences (\(\Delta T\)) following the start of fluid circulation for the same \(\Delta T_{\text{on}}\) setpoint. Moreover, \(\Lambda_{\text{pv},\text{off}}\) and \(\Lambda_{\text{pv},\text{on}}\) decrease and increase with \(G_{T}\), respectively, and more so for higher PV conversion efficiencies and lower temperature coefficients, but less so for higher linear heat loss coefficients. In other words, the more thermally and electrically efficient the collectors are and temperature-sensitive the PV conversion efficiency is, the higher the difference between setpoint selection for hybrid and non-hybrid operation modes is.
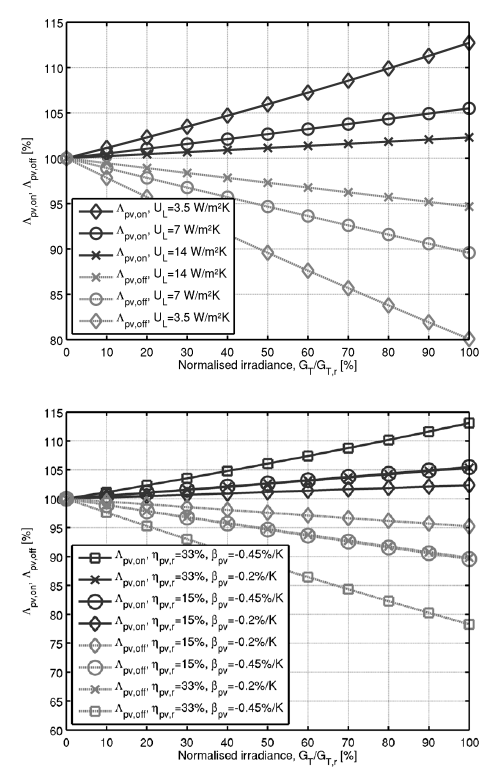
Quantitatively, \(\Delta T_{\text{off},min}\) and \(\Delta T_{\text{on},min}\) for hybrid operation do not appear to deviate significantly from their values for non-hybrid operation, even at high \(G_{T}\). For the reference system and \(G_{T}\) values up to 1000 W/m2, \(\Delta T_{\text{off},min}\) and \(\Delta T_{\text{on},min}/\Delta T_{\text{off}}\) decreased by as much as 10.4% (relative) and increased by up to 5.5% (relative), respectively, whereas for the system variations considered for Figure 2, the limits were 19.9% and 13.1%, respectively.
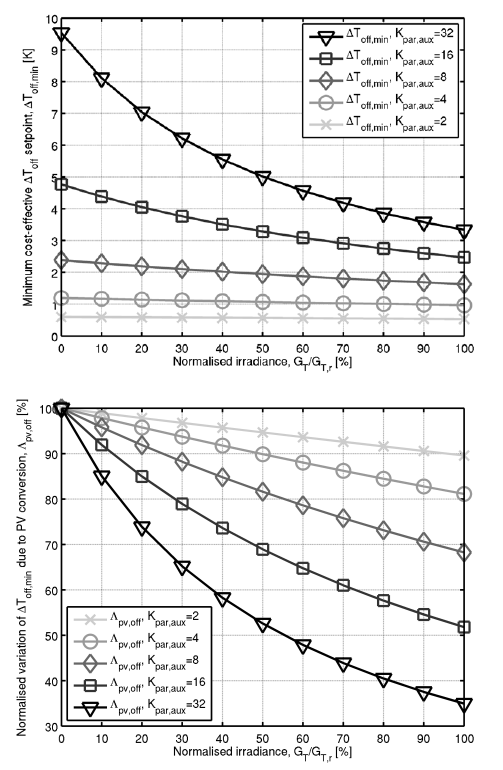
In turn, factors such as \(K_{\text{pv},\text{el}}\), \(\eta_{\text{el},\text{bos}}\) and \(K_{\text{par},\text{aux}}\) cause higher \(\Lambda_{\text{pv},\text{off}}\) reductions with \(G_{T}\) as they increase. Each of these factors exerts the same influence on \(\Lambda_{\text{pv},\text{off}}\) but only \(K_{\text{par},\text{aux}}\) can be reasonably expected to change significantly between systems and, unlike the others, it simultaneously influences \(\Delta T_{\text{off},min}\) for hybrid and non-hybrid operation, in accordance the inequalities (20) and (1), respectively. For example, a 16-fold \(K_{\text{par},\text{aux}}\) increase over the reference value – illustrated in Figure 3 – led the \(\Delta T_{\text{off},min}\) for hybrid operation to decrease by as much as roughly 65% at GT=1000 W/m2 compared to 10% for the reference case, while the GT-insensitive \(\Delta T_{\text{off},min}\) for non-hybrid operation increased 16-fold (1500%). Consequently, the effect of PV conversion is also more significant in absolute terms for high \(K_{\text{par},\text{aux}}\). The energy price relations are, however, more commonly in line with the reference case and thus the \(\Delta T_{\text{off},min}\) variations are not expected to be as pronounced in typical systems.
Numerical Method Using the Extended Perers Model
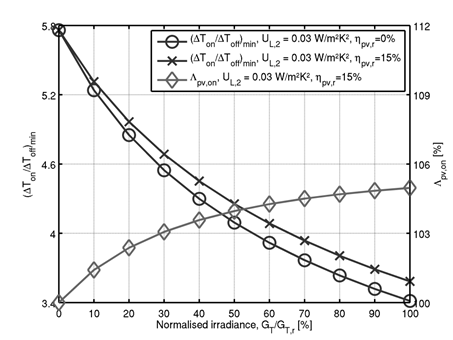
The numerical method was able to reproduce the analytical results, as illustrated in Figure 4. However, by considering a non-negligible collector heat loss temperature dependence (\(U_{L,2} \neq 0\) W·m-2·K-2), the numerical method produced more nuanced results though ultimately leading to the same conclusions: cost-effective and stable operation of PV-T systems generating electricity is compatible with lower \(\Delta T_{\text{off}}\) setpoints and requires higher \(\Delta T_{\text{on}}\) setpoints, respectively, than for those not generating electricity or equivalent non-hybrid systems.
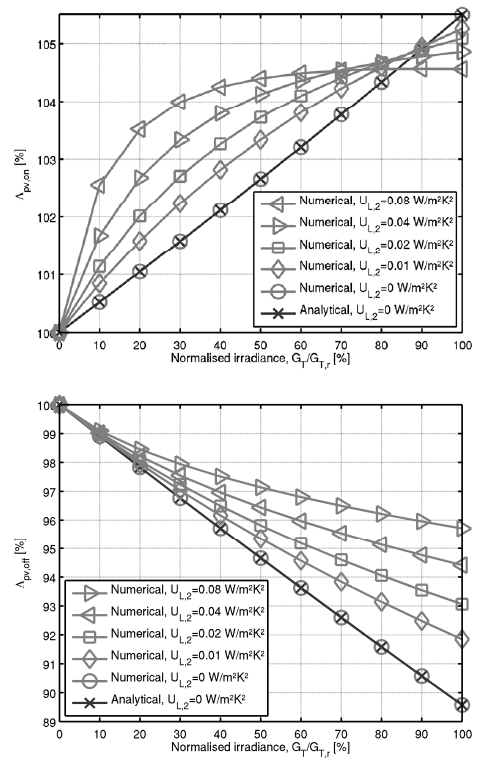
Moreover, the factors \(\Lambda_{\text{pv},\text{off}}\) and \(\Lambda_{\text{pv},\text{on}}\) in this case were of the same order of magnitude as those obtained using the analytical method, though other differences are worth highlighting. In particular, the numerically-determined \(\Lambda_{\text{pv},\text{off}}\) and \(\Lambda_{\text{pv},\text{on}}\) do not vary linearly with \(G_{T}\) for collectors with a non-negligible \(U_{L,2}\). Instead, the \(\Lambda_{\text{pv},\text{off}}\) variation with \(G_{T}\) is increasingly less abrupt, for the same \(U_{L,1}\), whereas \(\Lambda_{\text{pv},\text{on}}\) exceeds the linear solutions at low \(G_{T}\) levels but falls below them near reference irradiance levels, as exemplified in Figure 4.
Hence, the numerical method results for the condition for cost-effective operation appear to be consistent with those obtained using the analytical method in the sense that higher collector heat losses reduce the differences between hybrid and non-hybrid operation. This outcome reflects the fact that higher collector heat losses essentially contribute to passive collector cooling, which benefits PV generation independently of fluid circulation, and for this reason, there are increasingly fewer incentives to prolong fluid circulation at higher irradiance levels, since this potentiates higher temperatures and thus enhances quadratic heat losses.
On the other hand, the additional complexity observed in the numerical \(\Lambda_{\text{pv},\text{on}}\) estimates can be linked to \(\Delta T_{\text{on},min}\) decreases with \(G_{T}\) for hybrid and non-hybrid operation, as shown in Figure 5, which only occurred in case of a non-negligible \(U_{L,2}\). This means the \(\Delta T_{\text{on},min}\) increase due to PV generation (translated by \(\Lambda_{\text{pv},\text{on}}\)>1) proved insufficient to counter the decrease with \(G_{T}\) attributed to a non-negligible \(U_{L,2}\). In other words, the minimum \(\Delta T_{\text{on}}\) setpoint for cycling-free operation of PV-T systems generating electricity is slightly higher than for non-hybrid operation or equivalent non-hybrid systems but can nonetheless decrease with \(G_{T}\) if \(U_{L,2}\) is not negligible.
DISCUSSION
The effect of PV conversion on the conditions for cost-effective and cycling-free operation of PV-T systems, determined using the analytical and numerical methods described, can be predicted to be conservative or lacking in practical relevance in some situations. In general, PV generation in PV-T systems almost certainly anticipates and continues beyond the start and end of fluid circulation, respectively, meaning it likely has repercussions for setpoint selection, however small. However, one reason why the repercussions are likely limited concerns the mostly monotonically varying nature of \(\Lambda_{\text{pv},\text{on}}\) and \(\Lambda_{\text{pv},\text{off}}\) with \(G_{T}\), meaning the most significant differences take place at high irradiance levels not generally associated with the start and end of fluid circulation in many systems.
Similarly, the assumption of a negligible collector heat capacity implies swift PV conversion efficiency and respective revenue reductions following transitions from fluid circulation to stagnation and vice-versa. In practice, however, the repercussions from a transition from fluid circulation to stagnation are (as much as 30 minutes) slower to set in due to thermal inertia, at which point circulation is possibly no longer cost-effective, and lower in magnitude if \(G_{T}\) is decreasing, as in a typical late afternoon shutdown (Zondag and van Helden, 2002). Also, the \(\Delta T_{\text{off},min}\) reduction with \(G_{T}\) may not have practical significance in typical high-flow PV-T systems for which low \(\Delta T_{\text{off}}\) setpoints (< 3 K) are already cost-effective – according to Eq. (1) – since compliance is generally handled conservatively in light of model limitations, parameter uncertainty, the limited thermal performance sensitivity to low \(\Delta T_{\text{off}}\) setpoints (≈ 1 K), and temperature measurement tolerances (1-3 K) (Winn, 1983; Hirsch, 1985; Peuser et al., 2002). On the other hand, the condition for cycling-free operation is generally regarded as merely indicative, if not unreliable, hence taking the effect of PV conversion into consideration would be of little practical consequence (Duffie and Beckman, 2013; Schiller et al., 1980; Winn, 1983).
Among the aforementioned factors, measurement errors can limit the ability of controllers to take advantage of the predicted effect of PV conversion on the conditions for cost-effective and cycling-free operation, and reap potential rewards, however small. As noted above, this is arguably more important concerning the former since cycling-free operation is generally not a priority in practice. The basic rationale for this is that a low effective \(\Delta T\) measurement tolerance is desirable to take advantage of the lower \(\Delta T_{\text{off}}\) setpoints enabled by PV conversion in the least conservative way possible. The same can be said about pump efficiency developments (lower \(P_{\text{pump}}\)), which would ideally allow ST systems to operate cost-effectively for longer (lower \(\Delta T_{\text{off},min}\)), but in practice, the potential is limited by the sensors’ measurement tolerances. The same argument applies even more forcefully to direct PV-T systems since their minimum setpoints are lower than for indirect PV-T systems, and thus their variation due to PV operation has a correspondingly lower practical relevance (Beckman et al., 1994; Kalogirou, 2009).
On the other hand, there is scant evidence to suggest anything more than marginal thermal and electrical performance enhancements would result in typical Summer-sized high-flow PV-T systems by taking into account the effect of PV conversion on setpoint selection. This assessment is based on the limited thermal performance sensitivity of non-hybrid systems to low \(\Delta T_{\text{off}}\) setpoints as documented by Hirsch (1985) and others, the comparable thermal performance of hybrid and non-hybrid collectors of equivalent designs, the reduced \(\Delta T_{\text{off},min}\) variation in absolute terms predicted for PV-T systems generating electricity relative to non-hybrid operation, and the generally low cell efficiency temperature coefficients. Naturally, this assessment is likely less valid for some low-flow PV-T systems and/or those bound to use comparatively expensive parasitic energy (high \(K_{\text{par},\text{aux}}\)) since for these the \(\Delta T_{\text{off},min}\) reduction will be more noticeable. In any case, there are reasons to consider these findings as having a marginal effect on setpoint selection for PV-T systems but they nevertheless indicate at least slightly different setpoints should be used. In particular, this process should be conducted using a representative irradiance level for each system, which should be at least as high as the minimum irradiance level for useful heat collection (Winn, 1993).
CONCLUSIONS
Analytical and numerical methods were developed to aid the differential temperature controller setpoint selection process for active grid-connected PV-T systems. These methods rely on the Florschuetz model and an extended Perers model to reproduce the conditions for stable and cost-effective operation in PV-T systems generating electricity. According to the methods, the conditions can be met using lower \(\Delta T_{\text{off}}\) setpoints and require higher \(\Delta T_{\text{on}}\) setpoints, respectively, than for PV-T systems not generating electricity or equivalent non-hybrid ST systems, and more so at higher irradiance levels. Conversely, the minimum setpoints’ normalised variation relative to the case of non-hybrid operation was limited to double-digit percentages in a sensitivity analysis on key system parameters for a reference indirect PV-T system. In turn, setpoint selection for direct PV-T systems is predicted to be even less sensitive to electricity generation since their minimum setpoints are lower than for indirect PV-T systems.
At the same time, the influence of electricity generation on setpoint selection determined using the above-named methods can be reasoned to be inflated or of limited practical relevance. This conclusion stems from this study’s modelling assumptions, the limited performance sensitivity to controller setpoints, and the preferred conservative design approach to deal with parameter uncertainty and temperature measurement tolerances. In conclusion, the effect of pump operation on electricity generation is not predicted to be a determining factor for differential temperature controller setpoint selection in active PV-T systems.
ACKNOWLEDGEMENTS
The current study was made possible by a doctoral grant (reference SFRH/BD/76747/2011) issued by the Foundation for Science and Technology (FCT). The authors would also like to thank the National Laboratory of Energy and Geology (LNEG), the Faculty of Science and Technology, New University of Lisbon (FCT-UNL) and the Centre of Technology and Systems (CTS) at UNINOVA for the support provided.
References
- Alcone, J. M., Herman, R. W. (1981). Simplified methodology for choosing controller set-points, in R. L. Reid, L. M. Murphy, D. S. Ward (eds) Proceedings of the ASME Solar Energy Division Third Annual Conference on Systems Simulation, Economic Analysis/Solar Heating and Cooling Operational Results, Reno, Nevada, April 27-May 1, 1981. New York, New York: American Society of Mechanical Engineers, 345-347.
- Araújo, A. and Pereira, V. (2016). Solar thermal modeling for rapid estimation of auxiliary energy requirements in domestic hot water production: On-off flow rate control. Energy, 119, 637-651. https://doi.org/10.1016/j.energy.2016.11.025
- Araújo, A. and Pereira, V. (2017). Solar thermal modeling for rapid estimation of auxiliary energy requirements in domestic hot water production: Proportional flow rate control. Energy, 138, 668-681. https://doi.org/10.1016/j.energy.2017.07.109
- Badescu, V. (2008). Optimal control of flow in solar collector systems with fully mixed water storage tanks. Energy Convers. Manag., 49, 169-184. https://doi.org/10.1016/j.enconman.2007.06.022
- Badescu, V. (2017). Optimal Control in Thermal Engineering, 1st ed., Cham, Switzerland: Springer. https://doi.org/10.1007/978-3-319-52968-4
- Beckman, W. A., Thornton, J., Long, S. and Wood, B. D. (1994). Control problems in solar domestic water systems. Sol. Energy, 53 (3), 233-236. https://doi.org/10.1016/0038-092X(94)90629-7
- Chow, T. T., Chan, A. L. S., Fong, K. F., Lin Z., He, W. and Ji, J. (2009). Annual performance of building-integrated photovoltaic/water-heating system for warm climate application. Applied Energy, 86, 689-696. https://doi.org/10.1016/j.apenergy.2008.09.014
- de Vries, D. (1998). Design of a photovoltaic/thermal combi-panel. PhD thesis. Eindhoven: Technische Universiteit Eindhoven.
- Duffie, J. A. and Beckman, W. (2013). Solar Engineering of Thermal Processes, 4th ed., Hoboken, New Jersey: Wiley. https://doi.org/10.1002/9781118671603
- Dupeyrat, P., Ménézo, C., Fortuin, S. (2014). Study of the thermal and electrical performances of PVT solar hot water system. Energy and Buildings, 68, 751-755. https://doi.org/10.1016/j.enbuild.2012.09.032
- Eicker, U. (2003). Solar Technologies for Buildings, 1st ed., Chichester, West Sussex: Wiley. https://doi.org/10.1002/0470868341
- Florschuetz, L. W. (1979). Extension of the Hottel-Whillier model to the analysis of combined photovoltaic/thermal flat plate collectors. Sol. Energy, 22, 361-366. https://doi.org/10.1016/0038-092X(79)90190-7
- Haurant, P., Ménézo, C. and Dupeyrat, P. (2014). The PHOTOTHERM project: full scale experimentation and modelling of a photovoltaic - thermal (PV-T) hybrid system for domestic hot water applications. Energy Procedia, 48, 581-587. https://doi.org/10.1016/j.egypro.2014.02.068
- Haurant, P., Ménézo, C., Gaillard, L. and Dupeyrat, P. (2015). A numerical model of a solar domestic hot water system integrating hybrid photovoltaic/thermal collectors. Energy Procedia, 78, 1991-1997. https://doi.org/10.1016/j.egypro.2015.11.391
- Hirsch, U. T. (1985). Control strategies for solar water heating systems, MSc. thesis. Madison, Wisconsin: University of Wisconsin-Madison.
- Huang, B. J. (1994). Transient performance of solar systems with a bang-bang controller. Journal of the Chinese Society of Mechanical Engineering, 15 (5), 409-417.
- Huang, B. J., Lin, T. H., Hung, W. C. and Sun, F. S. (2001). Performance evaluation of solar photovoltaic/thermal systems. Sol. Energy, 70(5), 443-448. https://doi.org/10.1016/S0038-092X(00)00153-5
- IEA-SHC (n.d.) PVT Systems: Application of PVT Collectors and New Solutions in HVAC systems. Available at: http://task60.iea-shc.org/ (Accessed 17 April, 2018)
- Kahwaji, G. and Winn, C. B. (1986). Effect of the Cycling Rate on Energy Collection for Bang-Bang Controllers. J. Sol. Energy Eng., 108(3), 206-213. https://doi.org/10.1115/1.3268094
- Kalogirou, S. (2009). Solar Energy Engineering: Processes and Systems, 1st ed., Burlington, Massachusetts: Academic Press.
- Kicsiny, R. and Farkas, I. (2012). Improved differential control for solar heating systems. Sol. Energy, 86, 3489-3498. https://doi.org/10.1016/j.solener.2012.08.003
- Knudsen, S. (2002). Consumers’ influence on the thermal performance of small SDHW systems-Theoretical investigations. Sol. Energy, 73 (1), 33-42. https://doi.org/10.1016/S0038-092X(02)00018-X
- Magalhães, P. M. L. P., Martins, J. F. A. and Joyce, A. L. M. (2016). Comparative analysis of overheating prevention and stagnation handling measures for photovoltaic-thermal (PV-T) systems. Energy Procedia, 91, 346-355. https://doi.org/10.1016/j.egypro.2016.06.282
- Muralidhar, G. K., Nagaraju, J. and Mohan, S. (1989). Effectiveness of a Differential Temperature Controller on a Solar Water Heating System: An Experimental Study. J. Sol. Energy Eng., 111(1), 97-99. https://doi.org/10.1115/1.3268293
- Perers, B. (1993). Dynamic method for solar collector array testing and evaluation with standard database and simulation programs. Sol. Energy, 50 (6), 517-526. https://doi.org/10.1016/0038-092X(93)90114-4
- Peuser, F. A., Remmers, K.-H. and Schnauss, M. (2002). Solar Thermal Systems: Successful Planning and Construction, 1st ed., Berlin: Solarpraxis.
- Prapas, D. E., Veliannis, I., Evangelopoulos, A. and Sotiropoulos, B. A. (1995). Large DHW solar systems with distributed storage tanks. Sol. Energy, 55 (3), 175-184. https://doi.org/10.1016/0038-092X(95)00042-P
- Rockendorf, G., Sillmann, R., Podlowski, L. and Litzenburger, B. (1999). PV-hybrid and thermoelectric collectors. Sol. Energy, 67 (4-6), 227-237. https://doi.org/10.1016/S0038-092X(00)00075-X
- Schiller, S. R., Warren, M. L. and Auslander, D. M. (1979). Comparison of Proportional and On/Off Solar Collector Loop Control Strategies Using a Dynamic Collector Model, Lawrence Berkeley Laboratory, University of California, prepared for the U.S. Department of Energy under Contract W-7405-ENG-48. Manuscript submitted to the Journal of Solar Energy.
- Schiller, S. R., Warren, M. L. and Auslander, D. M. (1980). Comparison of Proportional and On/Off Solar Collector Loop Control Strategies Using a Dynamic Collector Model. J. Sol. Energy Eng., 102(4), 257-262. https://doi.org/10.1115/1.3266189
- Skoplaki, E. and Palyvos, J. A. (2009). On the temperature dependence of photovoltaic module electrical performance: A review of efficiency/power correlations. Sol. Energy, 83(5), 614-624. https://doi.org/10.1016/j.solener.2008.10.008
- Streicher, W. and Kaltschmitt, M. (2007). Solar thermal heat utilisation, in M. Kaltschmitt, W. Streicher, A. Wiese (eds), Renewable Energy: Technology, Economics and Environment, (pp. 123-170). Berlin: Springer-Verlag.
- Winn, C. B. (1983). The Effects of Temperature Settings on Cycling Rates for Bang-Bang Controllers. J. Sol. Energy Eng., 105(3), 277-280. https://doi.org/10.1115/1.3266378
- Winn, C. B. (1993). Controls in Active Solar Energy Systems, in Löf, G. (eds), Active Solar Systems, (81-149) Cambridge, Massachusetts: MIT Press.
- Zondag, H. A. and van Helden, W. G. J. (2002). Stagnation temperature in PVT collectors, in PV in Europe: from PV technology to energy solutions Conference and Exhibition, Rome, Italy, 7-11 October, 2002.
- Zondag, H., Bakker, M., van Helden, W., Affolter, P., Eisenmann, W., Fechner, H., Rommel, M., Schaap, A., Sørensen, H. and Tripanagnostopoulos, Y. (2005). PVT Roadmap: A European guide for the development and market introduction of PV-Thermal technology, Project Catapult.
How to cite this article
APA
Magalhães, P., Martins, J., & Joyce, A. (2019). On Differential Temperature Controller Setpoint Selection for Active Photovoltaic-Thermal (PV-T) Systems. European Journal of Sustainable Development Research, 3(1), em0066. https://doi.org/10.20897/ejosdr/3926
Vancouver
Magalhães P, Martins J, Joyce A. On Differential Temperature Controller Setpoint Selection for Active Photovoltaic-Thermal (PV-T) Systems. EUR J SUSTAIN DEV RES. 2019;3(1):em0066. https://doi.org/10.20897/ejosdr/3926
AMA
Magalhães P, Martins J, Joyce A. On Differential Temperature Controller Setpoint Selection for Active Photovoltaic-Thermal (PV-T) Systems. EUR J SUSTAIN DEV RES. 2019;3(1), em0066. https://doi.org/10.20897/ejosdr/3926
Chicago
Magalhães, Pedro, João Martins, and António Joyce. "On Differential Temperature Controller Setpoint Selection for Active Photovoltaic-Thermal (PV-T) Systems". European Journal of Sustainable Development Research 2019 3 no. 1 (2019): em0066. https://doi.org/10.20897/ejosdr/3926
Harvard
Magalhães, P., Martins, J., and Joyce, A. (2019). On Differential Temperature Controller Setpoint Selection for Active Photovoltaic-Thermal (PV-T) Systems. European Journal of Sustainable Development Research, 3(1), em0066. https://doi.org/10.20897/ejosdr/3926
MLA
Magalhães, Pedro et al. "On Differential Temperature Controller Setpoint Selection for Active Photovoltaic-Thermal (PV-T) Systems". European Journal of Sustainable Development Research, vol. 3, no. 1, 2019, em0066. https://doi.org/10.20897/ejosdr/3926

 Full Text (PDF)
Full Text (PDF)