Abstract
The main purpose of this paper is to conduct momentum and energy analysis on non-Newtonian fluid flow in a semi-permeable medium between two infinite vertical flat plates considering the influences of medium porosity, heat source and magnetic field. In this study, porosity, heat source and magnetic field terms are considered to be variable. Initially, partial differential equations of momentum and energy are derived and turned into ordinary differential equations utilizing a similarity solution. Afterwards, a system of differential equations is solved by Least Square Method (LSM) and subsequently reliable functions are proposed for temperature and velocity distributions. To assess the precision of this method, the equations are also solved by a numerical method and an analytical approach known as Galerkin Method (GM). Regarding the comparisons, it can be implied that when the values of magnetic field, heat source and porosity are constant along the channel width, both LSM and GM methods are efficient and appropriate agreement is observed between the results. However, for the case in which these parameters linearly vary along the channel width, Galerkin approach shows more accurate results. Ultimately, the influences of Hartman number, porosity and heat source parameters on the velocity and temperature distributions are discussed.
License
This is an open access article distributed under the Creative Commons Attribution License which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Article Type: Research Article
EUR J SUSTAIN DEV RES, Volume 2, Issue 3, 2018, Article No: 33
https://doi.org/10.20897/ejosdr/2665
Publication date: 17 Jul 2018
Article Views: 3911
Article Downloads: 2671
Open Access HTML Content References How to cite this articleHTML Content
INTRODUCTION
Natural convection is a mechanism of heat transport in which no external source influences the fluid motion. In fact, density difference due to the gravitational field is the major causality of this type of heat transport. Due to its potential applications in industry and engineering, this mechanism has attracted a great deal of attentions among researchers. In many cases, accurate anticipation of the behavior of fluid flows can remove harmful effects such as mechanical noises and vibrations from industrial systems (Jianu and Rosen, 2017). A very conventional industrial application of natural convection is free cooling of electronic devices. This heat transfer mechanism can exist in small-scale devices such as computer chips to large-scale physical systems such as geothermal systems, heat exchangers, chemical catalytic reactors, fibre and granular insulation, packed beds, and petroleum reservoirs. In the last couple of decades, natural convection heat transfer for Newtonian and non-Newtonian fluids streaming between two infinite parallel vertical plates has been studied by different researchers. In these systems, heat is transferred by natural convection mechanism from vertical plates to fluids. Analysis of this mechanism is significant especially when the moving fluid is minimally affected by forced convection (McCabe et al., 1993). Natural convection heat transfer between vertical flat plates was analysed for several different non-Newtonian fluids by Bruce and Na (Bruce and Na, 1967). In another investigation, they considered and analysed several natural convection problems in laminar regimes (Shenoy and Mashelkar, 1982). Rajagopal (Rajagopal and Na, 1985) conducted a thermodynamic analysis on different constitutive functions in the area of fluid mechanics. It should be pointed out that in fluid mechanics problems, to yield reliable results, inherent non-linear behavior of systems must be considered. However, solving nonlinear equations is often very difficult. To overcome the complexities, various methods such as instance Homotopy Perturbation Method (HPM) (Nayfeh, 1973; Ganji et al., 2010; Rafei and Ganji, 2006; He, 2006; Soltanian et al., 2010; Esmaeilpour and Ganji, 2007; Ganji et al., 2007; Ganji et al., 2006), Variational Iteration Method (VIM) (Wang and He, 2007), Homotopy Analysis Method (HAM) (Hassan and Rashidi, 2013; Shahzad and Ramzan, 2012), Adomian Decomposition Method (ADM) (Abbasbandy, 2007), Least Square Method (Shi and Ren, 2010), Galerkin Method (Hessari, 2014) and Collocation Method (CM) (Petroudi et al., 2014) have been introduced by different researchers. It is worth mentioning that the aforementioned methods offer accurate successive approximations for solution of ODEs. Etbaeitabari and Domairy (Etbaeitabari et al., 2013) employed VIM to evaluate the natural convection of a non-Newtonian fluid streaming between two infinite vertical plates (Etbaeitabari et al., 2013). Ziabakhsh and Domairy (Ziabakhsh and Domairry, 2009) analytically investigated the natural convection of a non-Newtonian fluid between two infinite parallel vertical flat plates considering the nature of the fluid. Hatami et al. (Hatami et al., 2014) numerically and analytically performed a heat transfer and flow analysis on a non-Newtonian third grade nanofluid flow in porous medium considering magnetic field. Sheikholeslami and Ganji (Sheikholeslami and Ganji, 2015) analytically solve the problem of nanofluid hydrothermal behavior in presence of magnetic field and Brownian motion of nanoparticles using Differential Transformation Method. Sheikholeslami et al. (Sheikholeslami et al., 2015) used differential transformation method to develop a theoretical solution for the case of laminar steady magnetohydrodymanics nanofluid streaming in a semi-permeable channel. Azimi et al. (Azimi et al., 2014) analytically studied the heat transfer of an unsteady nanofluid flow between two moving parallel plates applying Galerkin Optimal Homotopy Asymptotic Method. In another paper, Azimi et al. (Azimi and Riazi, 2016) proposed an analytical solution for the problem of a steady nanofluid streaming through a convergent-divergent channel utilizing Reconstruction of Variational Iteration method. Shahriari et al. (Shahriari et al., 2018) analytically investigated the effect of viscous dissipation on temperature distribution of a two-dimensional unsteady nanofluid streaming between two moving parallel plates utilizing Akbari-Ganji Method. The main purpose of the present paper, for the first time, is to carry out a momentum and energy analysis on non-Newtonian fluid flow between two infinite vertical flat plates in a changeable semi-permeable medium considering variable heat source and magnetic field terms. Initially, partial differential equations of momentum and energy are derived and turned into ordinary differential equations using a similarity solution. Afterwards, a system of differential equations is solved by LSM and subsequently reliable functions are presented for temperature and velocity distributions. In order to evaluate the reliability of this method, the governing equations are also solved and compared by a numerical method and an analytical approach known as GM. Subsequently, the influences of Hartman number, porosity and heat source parameters on the velocity and temperature distributions are presented. Finally, variations of velocity with change types of porosity and magnetic field are studied.
GOVERNING EQUATIONS
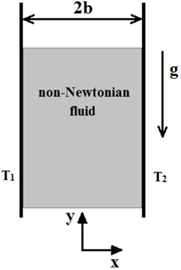
Figure 1 illustrates the schematic of the problem analysed in the current paper. As can be seen in this figure, the system includes two vertical flat plates (the distance between the plates is considered to be 2b) and a non-Newtonian fluid streaming between the plates. In this investigation, a steady, incompressible, non-Newtonian fluid flow between two parallel vertical plates in a semi-permeable medium with variable heat source and magnetic field terms is considered. The schematic of the problem is shown in Figure 1. The temperatures of the walls located at \(x = + b\) and \(x = - b\) are constant and assumed to be \(T_{2}\) and \(T_{1}\) (\(T_{1}\)>\(T_{2}\)), respectively. This temperature difference results in upward motion of fluid near the wall at \(x = - b\) and downward motion of fluid near the wall at \(x = + b\).
Generally, a viscous fluid is governed by continuity and Navier–Stokes equations. Since the fluid is considered to be incompressible, the conservation equations of momentum and energy are stated as follows (Rajagopal and Na, 1985; Hatami et al., 2014; Sheikholeslami and Ganji, 2015):
| \[\rho_{f}\left( \frac{\partial u}{\partial t} + u.\nabla u \right) = divT^{*} - \frac{\text{μφ}}{k^{*}}\left( 1 + \lambda_{r}\frac{\partial}{\partial t} \right)u + \rho_{f}\left\lbrack 1 - \beta_{T}\left( T - T_{m} \right) \right\rbrack g + J \times B\] | (1) |
| \[{(\rho c)}_{f}\left( \frac{\partial T}{\partial t} + u.\nabla T \right) = - k\nabla^{2}T + T^{*}.L + Q_{0}(T - T_{m})\] | (2) |
where \(\varphi\) and \(Q_{0}\) are porosity of medium and heat source parameter, respectively. Stress in a third-grade non-Newtonian fluid (\(T^{*}\)) is presented in the following (Hatami et al., 2014):
| \[T^{*} = - pI + \left\lbrack \mu + \beta_{3}\left( \text{tr}A_{1}^{2} \right) \right\rbrack A_{1} + \alpha_{1}A_{2} + \alpha_{2}A_{1}^{2}\] | (3) |
where \(\beta_{3}\), \(\alpha_{1}\) and \(a_{2}\) are temperature-dependent material modules which. In Eq. 3, \(- pI\) represents the spherical stress related to the restraint of incompressibility and \(L\) is velocity gradient. The definitions of the kinematical tensors, \(A_{1}\) and \(A_{2}\), can be found in (Hatami et al., 2014).
Variable magnetic field, porosity of medium and heat source are defined as follows:
| \[\begin{matrix} J \times B = - \sigma B_{0}^{2}u\left( 1 - \frac{x}{b} \right), & \frac{\text{μφ}}{k^{*}}u = \frac{\text{μφ}}{k^{*}}\left( 1 - \frac{x}{b} \right)u, & Q = Q_{0}(T - T_{m}) \\ \end{matrix}\] | (4) |
By using the following similarity variables, the governing momentum and energy equations can be defined in simpler forms (Rajagopal and Na, 1985):
| \[\begin{matrix} U = \frac{u}{u_{0}}, & \eta = \frac{x}{b}, & \theta = \frac{T - T_{m}}{T_{1} - T_{2}} \\ \end{matrix}\] | (5) |
By substituting the above parameters into the Navier–Stokes and energy equations, following equation are obtained:
| \[\frac{d^{2}U}{d\eta^{2}} + 6\delta\left( \frac{\text{dU}}{\text{dη}} \right)^{2}\frac{d^{2}U}{d\eta^{2}} + \theta - PU\left( 1 - \eta \right) - \text{Ha}^{2}U(1 - \eta) = 0\] | (6) |
| \[\frac{d^{2}\theta}{d\eta^{2}} + Ec.Pr\left( \frac{\text{dU}}{\text{dη}} \right)^{2}\frac{d^{2}U}{d\eta^{2}} + 2\delta E.Pr\left( \frac{\text{dU}}{\text{d\ η}} \right)^{4} + M\theta = 0\] | (7) |
where \(\Pr\), \(\text{Ec}\), \(\delta\), \(P\), \(\text{Ha}\) and \(M\) are Prandtl number, Eckert number, dimensionless non-Newtonian viscosity, dimensionless porosity parameter, Hartman number and dimensionless heat source parameter, respectively. These parameters are defined in the following:
| \[\begin{matrix} Ec = \frac{{U_{0}}^{2}}{c(T_{1} - T_{2})}, & Pr = \frac{\text{μc}}{k}, & \delta = \frac{6\beta_{3}{U_{0}}^{2}}{\mu b^{2}}, & P = \frac{\varphi b^{2}}{k^{*}}, & M = \frac{Q_{0}b^{2}}{k}, & Ha = B_{0}b\sqrt{\frac{\sigma_{f}}{\mu}} \\ \end{matrix}\] | (8) |
Accurate boundary conditions for this problem are presented in the following (Rajagopal and Na, 1985):
| \[U = 0,\theta = + \frac{1}{2}\ \text{at}\ \eta = - 1\] | (9) |
| \[U = 0,\ \theta = - \frac{1}{2}\ \text{at}\ \eta = + 1\] | (10) |
In this study, for solving the coupled and non-linear Eqs. (6) and (7), least square and Galerkin methods are used.
THEORETICAL METHODS
Least square and Galerkin methods are analytical methods operating based on Weighted Residuals Methods. In these methods, a differential operator represented by \(D\) is applied on the function of \(u\) to generate function \(p\).
| \[D\left( u\left( x \right) \right) = p(x)\] | (11) |
where function \(u\) is approximated by \(\widetilde{u}\) and is a linear combination of a set of functions.
| \[u \cong \widetilde{u} = \sum_{i = 1}^{n}{c_{i}\varphi_{i}}\] | (12) |
Since \(p\) cannot be calculated by applying operator \(D\) on the approximated function \(u\), an error will be appeared in the calculations which can be defined as follows:
| \[E\left( x \right) = R\left( x \right) = D\left( \widetilde{u}\left( x \right) \right) - p(x) \neq 0\] | (13) |
Minimizing the average residual of Eq. 13 is the main purpose of these three procedures.
| \[\begin{matrix} \int_{}^{}{R\left( x \right)W_{i}\left( x \right) = 0}, & i = 1,2,\ldots,n \\ \end{matrix}\] | (14) |
In LSM, \(W_{i}\) can be calculated by the following correlation:
| \[\begin{matrix} W_{i} = \frac{\partial R}{\partial c_{i}}, & i = 1,2,\ldots,n \\ \end{matrix}\] | (15) |
In GM, \(W_{i}\) is defined as follows:
| \[\begin{matrix} W_{i} = \frac{\partial\widetilde{u}}{\partial c_{i}}, & i = 1,2,\ldots,n \\ \end{matrix}\] | (16) |
It is notable that the number of weight functions are equal to the number of unknown parameters of the approximated function which must satisfy the considered initial and boundary conditions.
RESULTS AND DISCUSSION
Comparison of Analytical and Numerical Results
As previously expressed, LSM is used for solving the non-linear governing equations. Analysis and solution of the governing equations are implemented in Matlab. By applying the boundary conditions, following approximated functions are considered for velocity and temperature distributions, respectively. It is worth mentioning that these functions are calculated by using try-and-error technique.
| \[U = 0.5\eta + c_{1}\left( \eta^{2} - 1 \right) + c_{2}\left( {\eta - \eta}^{3} \right)\] | (17) |
| \[\theta = c_{3}\left( \eta^{2} - 1 \right) + c_{4}\left( {\eta - \eta}^{3} \right)\] | (18) |
By using the velocity and temperature approximated functions and applying the LSM, unknown coefficients in Eqs. 17 and 18 will be obtained. For validation purpose, the values of non-dimensionalized numbers including \(\delta\), \(\Pr\), \(\text{Ha}\), \(P\), \(M\) and \(\text{Ec}\) are taken to be unity and constant. By doing some algebraic computations, following equations are achieved for velocity and temperature distributions:
| \[U = - 1.565 \times 10^{- 5}\left( \eta^{2} - 1 \right) - 0.0758\left( {\eta - \eta}^{3} \right)\] | (19) |
| \[\theta = 0.5\eta - 8.3463 \times 10^{- 5}\left( \eta^{2} - 1 \right) - 0.0885\left( {\eta - \eta}^{3} \right)\] | (20) |
Results calculated by the current numerical and analytical solutions for flow velocity and temperature are indicated in Figures 2 and 3, respectively. As can be observed in these figures, there is an appropriate agreement between the numerical and analytical results. Hence, it can be concluded that for this problem LSM is an efficient technique for solving the momentum and energy equations.
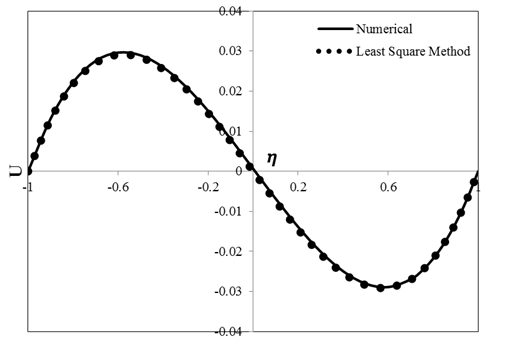
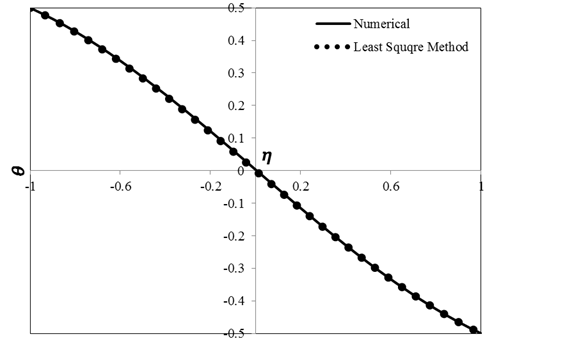
Tables 1 and 2 list the values of velocity and temperature calculated by using the numerical and analytical approaches which includes LSM and GM for two different cases. As presented in Table 1, for the first case, \(\delta = Pr = Ec = M = P = Ha = 1\). In this case, porosity and magnetic field parameters are constant along the channel width. The average error related to LSM for non-dimensionalized functions of velocity and temperature are found to be 0.034% and 0.16% in this case, respectively. The average error related to GM for non-dimensionalized functions of velocity and temperature are found to be 0.035% and 0.17%, respectively. By comparing the values of errors, it is implied that precision and efficiency of both of the methods are considerable high.
|
Table 1. Results obtained by LSM, GM and numerical (Num) methods for U(𝞰) and θ(𝞰) when \(\mathbf{\delta = Pr = Ec = M = P = Ha = 1}\) and are constant along the channel width
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Table 2. Results obtained by LSM, GM and numerical (Num) methods for U(𝞰) and θ(𝞰) when \(\mathbf{\delta = Pr = Ec = M = P = Ha = 1}\) and vary along the channel width
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
As listed in Table 2, calculations are conducted for the case in which\(\ \delta = Pr = Ec = M = P = Ha = 1\). For this case, porosity and magnetic field parameters are proportional to \(1 - \eta\) and linearly vary along the channel width. In this case the average error related to LSM for velocity and temperature functions are found to be 0.5% and 3.36%, and for GM the values of average error are found to be 0.088% and 0.42%, respectively. Results show that when porosity, heat source and magnetic field parameters are constant along the channel width, both of the method are efficient. Nevertheless, for the case in which the parameters vary linearly, Galerkin method possesses better performance.
Effects of Porosity on Velocity and Temperature Distributions
Figures 4 and 5 describe the influences of dimensionless porosity parameter on the velocity and temperature when the values of the other non-dimensionalized parameters including \(\delta\), Pr, Ec, Ha and M are unity. According to these figures, it can be seen that porosity parameter which appears in the form of \(PU(1 - \eta)\) linearly varies. With regard to Figure 4, it can be observed that with an increase in the value of porosity parameter, velocity reduces. In other words, rising this parameter results in an increment in porosity and a reduction in permeability leading to a greater resistance against the fluid flow and subsequently a decline in the value of velocity. The effect of channel width on the temperature distribution for several values of porosity parameter is delineated in Figure 5. As can be seen in Figure 5, variation of temperature with channel width for different values of porosity parameters are very close to each other. Therefore, it can be concluded that porosity has negligible impact on the flow temperature.
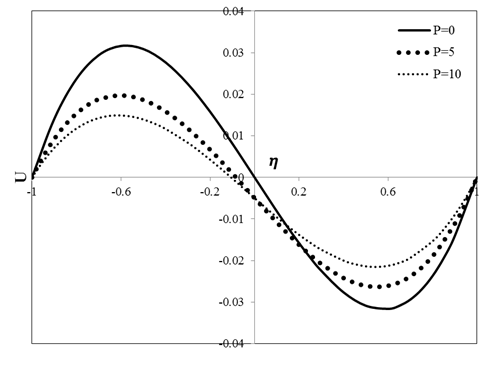
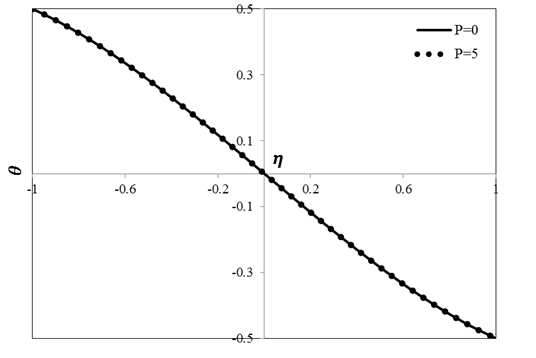
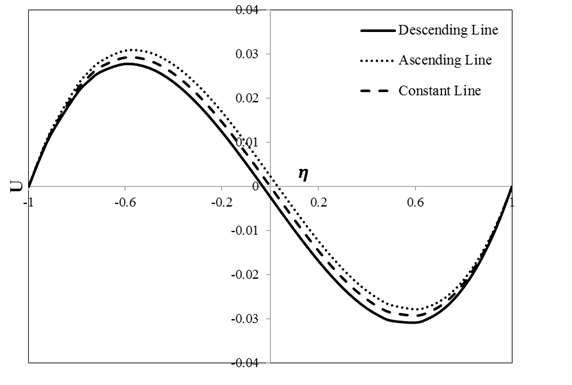
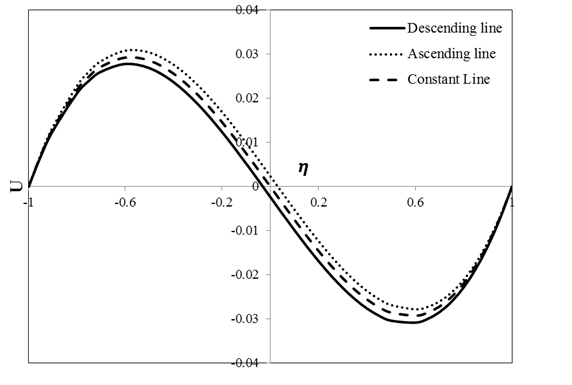
Figure 6 depicts the variation of velocity with position for several change types of porosity. In descending order, constant value and ascending order of porosity, porosity parameters are appeared in forms of\(\ PU(1 - \eta)\), \(\text{PU}\) and \(PU(\eta + 1)\) in the momentum equation, respectively. As can be seen in Figure 6, when porosity parameter is constant, velocity distribution is symmetric along the channel width. In descending order of porosity, velocity of the flow is zero before reaching the centerline of the channel and also on the left-hand side of the centerline. In this case, the value of resistance force due to the flow impermeability on the left-hand side of the centerline is greater on the left-hand side of the centerline. In this regard, velocity of the flow will be zero in this position. In ascending order of porosity, velocity of the flow is zero on the right-hand side of the centerline.
Effects of Heat Source Term on Velocity and Temperature Distributions
In Figures 7 and 8, the influences of non-dimensionalized heat source parameter on velocity and temperature distributions when the other parameters including\(\ \delta\), Ha, P, Pr and Ec are unity are indicated. Regarding Figure 7, with an increment in the value of heat source parameter, velocity of flow reduces along the channel width. The reason is that any change in temperature due to existence of heat source will lead to remarkable variations in buoyancy force and subsequently the flow velocity. With respect to Figure 8, it can be seen that an enhancement in the value of heat source parameter results in a reduction in temperature along the channel width. According to Figure 8, it must be pointed out that by adding heat source term in energy equation, temperature varies non-linearly. With increasing the value of heat source parameter, curvature of temperature distribution increases.
Effects of Magnetic Field on Velocity and Temperature Distributions
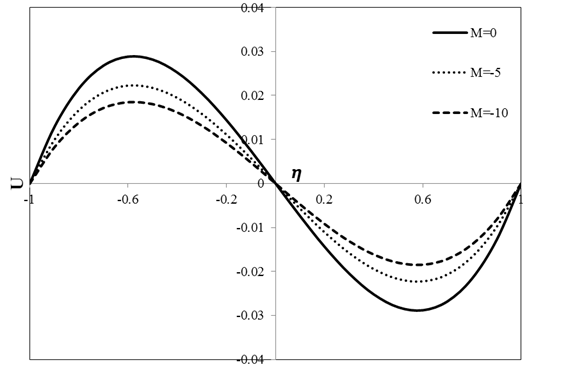
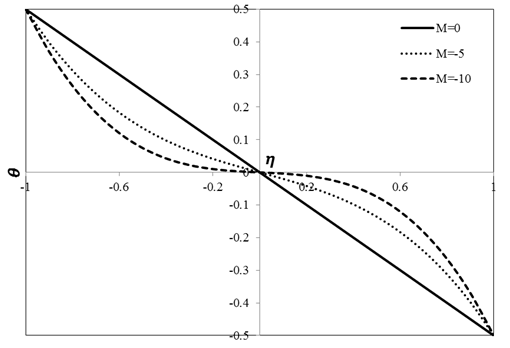
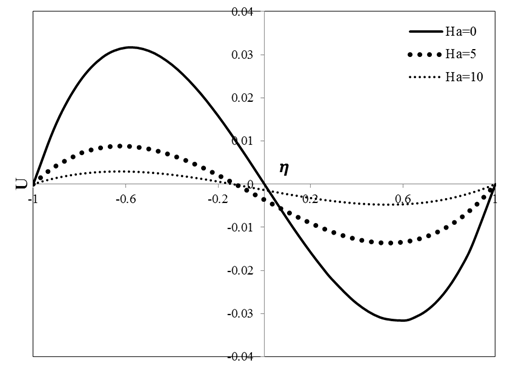
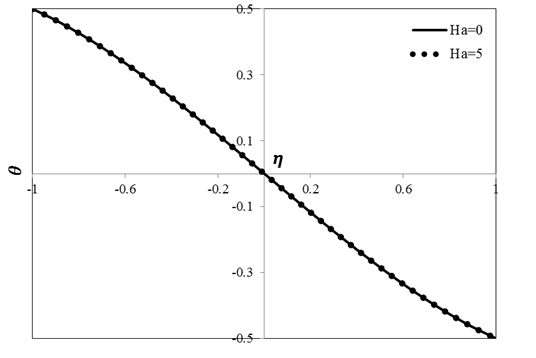
Figures 9 and 10 indicate the variations of velocity and temperature with position for different values of Hartman number. In these figures, all the considered dimensionless parameters except the Hartman number are assumed to be unity. In this case, magnetic field parameter is appeared in the form of \(\text{Ha}^{2}U(1 - \eta)\) in momentum equation. As shown in Figure 9, with an increment in the value of Hartman number, velocity in each point of the channel width declines. In fact, increasing the Hartman number rises the Lorentz force which is related to the magnetic field leading to an increment in resistance against the flow and subsequently reduction in the value of velocity. In Figure 10, the effect of Hartman number on temperature distribution is shown. According to this figure, Hartman number has insignificance impact on temperature. In other words, the effect of magnetic field on temperature is negligible. Figure 11 illustrates the variation of velocity with position for several change types of magnetic field. It should be noted that in this figure all the considered non-dimensionalized parameters are taken to be unity. In descending order, constant value and ascending order of magnetic field, this parameter is appeared in forms of\(\ \text{Ha}^{2}U(1 - \eta)\), \(\text{Ha}^{2}U\) and \(\text{Ha}^{2}U(\eta + 1)\), respectively, in the momentum equation. As can be seen in Figure 11, when magnetic field parameter is constant, velocity distribution is symmetric along the channel width. In descending order of magnetic field, velocity of the flow is zero before reaching the centerline of the channel as well as the left-hand side of the centerline. In this case, the value of resistance force due to the magnetic field on the left-hand side of the centerline is further. In this regard, velocity of the flow will be zero in this position. In ascending order of magnetic field, velocity of the flow is zero on the right-hand side of the centerline because of lower resistance in this region.
Nomenclature
| \[u\] | velocity in y direction |
| U | dimensionless velocity |
| \[P\] | porosity dimensionless parameter |
| \[M\] | heat source dimensionless parameter |
| \[\Pr\] | Prandtl number |
| \[b\] | half of plates distance |
| \[c\] | specific heat of the fluid |
| \[k\] | coefficient of conductivity |
| \[\text{Ec}\] | Eckert Number |
| \[\text{Ha}\] | Hartman Number |
| \[\Pr\] | Prandtl number |
| T | temperature field |
| \[T_{m}\] | mean temperature |
| \[u_{0}\] | inlet velocity |
| \[Q_{0}\] | heat source parameter |
| \[k^{*}\] | permeability |
| \[B_{0}\] | magnetic field |
Greek symbols |
|
| \[\delta\] | dimensionless non-Newtonian viscosity |
| \[\eta\] | dimensionless variable of distance |
| \[\mu\] | dynamic viscosity |
| \[\theta\] | dimensionless temperature |
| \[\rho_{f}\] | fluid density |
| \[\beta_{T}\] | coefficient of thermal expansion |
| \[\varphi\] | porosity |
| \[\sigma\] | electrical conductivity |
CONCLUSION
This study tried to perform a reliable analysis on solution of momentum and energy equations for non-Newtonian fluid flow between two infinite vertical flat plates taking into account the effects of the porosity of medium, heat source and magnetic field. In this paper, porosity, heat source and magnetic field terms are considered to be variable. In the first phase of this investigation, governing PDEs were converted into ODEs using a similarity solution. Afterwards, LSM was employed to solve a system of ODEs. To evaluate the accuracy of this method, the equations were also solved by an analytical approach called Galerkin method and a numerical technique. By comparing the results of these methods, it was revealed that for the case in which magnetic field, heat source and porosity terms are constant along the channel width, both of the analytical methods reached promising results. However, when the aforementioned terms linearly vary along the channel width, results obtained by Galerkin method were more accurate. Based on the results, with an increase in the value of porosity parameter, the velocity declined while the temperature profile varied constantly. Furthermore, enhancing the value of heat source parameter led to reductions in the values of velocity and temperature. It should be pointed out that by adding heat source term, a curvature appeared in temperature profile. In other words, the temperature distribution varied non-linearly considering this term and the profile curvature grew with rising the value of heat source parameter. With an increase in the value of Hartman number, velocity would reduce while temperature was constant. By enforcing variable porosity and magnetic field terms to momentum equation, velocity distribution would be non-symmetric and stagnation point shifted to the right or left-hand sides of the channel centerline. The position of stagnation point relative to the channel centerline was specified by ascending, descending and constant lines.
References
- Abbasbandy, S. (2007). A numerical solution of Blasius equation by Adomian’s decomposition method and comparison with homotopy perturbation method. Chaos, Solitons & Fractals, 31(1), 257-260. https://doi.org/10.1016/j.chaos.2005.10.071
- Azimi, M., Azimi, A. and Mirzaei, M. (2014). Investigation of the unsteady graphene oxide nanofluid flow between two moving plates. Journal of Computational and Theoretical Nanoscience, 11(10), 2104-2108. https://doi.org/10.1166/jctn.2014.3612
- Azimi, M. and Riazi, R. (2016). MHD copper-water nanofluid flow and heat transfer through convergent-divergent channel. Journal of Mechanical Science and Technology, 30(10), 4679-4686. https://doi.org/10.1007/s12206-016-0938-3
- Bruce, R. W. and Na, T. Y. (1967). Natural convection flow of Powell-Eyring fluids between two vertical flat plates. ASME.
- Esmaeilpour, M. and Ganji, D. D. (2007). Application of He's homotopy perturbation method to boundary layer flow and convection heat transfer over a flat plate. Physics Letters A, 372(1), 33-38. https://doi.org/10.1016/j.physleta.2007.07.002
- Etbaeitabari, A., Barakat, M., Imani, A. A., Domairry, G. and Jalili, P. (2013). An analytical heat transfer assessment and modeling in a natural convection between two infinite vertical parallel flat plates. Journal of Molecular Liquids, 188, 252-257. https://doi.org/10.1016/j.molliq.2013.09.010
- Ganji, D. D. (2006). The application of He's homotopy perturbation method to nonlinear equations arising in heat transfer. Physics Letters A, 355(4), 337-341. https://doi.org/10.1016/j.physleta.2006.02.056
- Ganji, D. D., Tari, H. and Jooybari, M. B. (2007). Variational iteration method and homotopy perturbation method for nonlinear evolution equations. Computers & Mathematics with Applications, 54(7), 1018-1027. https://doi.org/10.1016/j.camwa.2006.12.070
- Ganji, D. D., Rokni, H. B., Sfahani, M. G. and Ganji, S. S. (2010). Approximate traveling wave solutions for coupled Whitham–Broer–Kaup shallow water. Advances in Engineering Software, 41(7), 956-961. https://doi.org/10.1016/j.advengsoft.2010.05.008
- Hassan, H. N. and Rashidi, M. M. (2013). Analytical solution for three-dimensional steady flow of condensation film on inclined rotating disk by optimal homotopy analysis method. Walailak Journal of Science and Technology (WJST), 10(5), 479-498.
- Hatami, M., Hatami, J. and Ganji, D. D. (2014). Computer simulation of MHD blood conveying gold nanoparticles as a third grade non-Newtonian nanofluid in a hollow porous vessel. Computer Methods and Programs in Biomedicine, 113(2), 632-641. https://doi.org/10.1016/j.cmpb.2013.11.001
- He, J. H. (2006). Addendum: new interpretation of homotopy perturbation method. International Journal of Modern Physics B, 20(18), 2561-2568. https://doi.org/10.1142/S0217979206034819
- Hessari, P. (2014). First order system least squares method for the interface problem of the Stokes equations. Computers & Mathematics with Applications, 68(3), 309-324. https://doi.org/10.1016/j.camwa.2014.06.003
- Jianu, O. A. and Rosen, M. A. (2017). Preliminary Assessment of Noise Pollution Prevention in Wind Turbines Based on an Exergy Approach. European Journal of Sustainable Development Research, 1(2), 12. https://doi.org/10.20897/ejosdr.201712
- McCabe, W. L., Smith, J. C. and Harriott, P. (1993). Unit operations of chemical engineering (vol. 5, pp. 154). New York: McGraw-Hill.
- Nayfeh, A. H. (1973). Perturbation methods. Wiley, New York.
- Petroudi, I. R., Ganji, D. D., Nejad, M. K., Rahimi, J., Rahimi, E. and Rahimifar, A. (2014). Transverse magnetic field on Jeffery–Hamel problem with Cu–water nanofluid between two non parallel plane walls by using collocation method. Case Studies in Thermal Engineering, 4, 193-201. https://doi.org/10.1016/j.csite.2014.10.002
- Rafei, M. and Ganji, D. D. (2006). Explicit solutions of Helmholtz equation and fifth-order KdV equation using homotopy perturbation method. International Journal of Nonlinear Sciences and Numerical Simulation, 7(3), 321-328. https://doi.org/10.1515/IJNSNS.2006.7.3.321
- Rajagopal, K. R. and Na, T. Y. (1985). Natural convection flow of a non-Newtonian fluid between two vertical flat plates. Acta Mechanica, 54(3), 239-246. https://doi.org/10.1007/BF01184849
- Shahriari, G., Maghsoudi, P. & Sadeghi, S. (2018). Impact of Viscous Dissipation on Temperature Distribution of a Two-dimensional Unsteady Graphene Oxide Nanofluid Flow between Two Moving Parallel Plates Employing Akbari-Ganji Method. European Journal of Sustainable Development Research, 2(2), 24. https://doi.org/10.20897/ejosdr/81574
- Shahzad, A. and Ramzan, A. L. I. (2012). MHD flow of a non-Newtonian Power law fluid over a vertical stretching sheet with the convective boundary condition. Walailak Journal of Science and Technology (WJST), 10(1), 43-56.
- Shenoy, A. V. and Mashelkar, R. A. (1982). Thermal convection in non-Newtonian fluids. Advances in Heat Transfer, 15, 143-225. https://doi.org/10.1016/S0065-2717(08)70174-6
- Sheikholeslami, M. and Ganji, D. D. (2015). Nanofluid flow and heat transfer between parallel plates considering Brownian motion using DTM. Computer Methods in Applied Mechanics and Engineering, 283, 651-663. https://doi.org/10.1016/j.cma.2014.09.038
- Sheikholeslami, M., Azimi, M. and Ganji, D. D. (2015). Application of differential transformation method for nanofluid flow in a semi-permeable channel considering magnetic field effect. International Journal for Computational Methods in Engineering Science and Mechanics, 16(4), 246-255. https://doi.org/10.1080/15502287.2015.1048384
- Shi, D. and Ren, J. (2010). A least squares Galerkin–Petrov nonconforming mixed finite element method for the stationary Conduction–Convection problem. Nonlinear Analysis: Theory, Methods & Applications, 72(3), 1653-1667. https://doi.org/10.1016/j.na.2009.09.005
- Soltanian, F., Dehghan, M. and Karbassi, S. M. (2010). Solution of the differential algebraic equations via homotopy perturbation method and their engineering applications. International Journal of Computer Mathematics, 87(9), 1950-1974. https://doi.org/10.1080/00207160802545908
- Wang, S. Q. and He, J. H. (2007). Variational iteration method for solving integro-differential equations. Physics Letters A, 367(3), 188-191. https://doi.org/10.1016/j.physleta.2007.02.049
- Ziabakhsh, Z. and Domairry, G. (2009). Analytic solution of natural convection flow of a non-Newtonian fluid between two vertical flat plates using homotopy analysis method. Communications in Nonlinear Science and Numerical Simulation, 14(5), 1868-1880. https://doi.org/10.1016/j.cnsns.2008.09.022
How to cite this article
APA
Maghsoudi, P., Sadeghi, S., Rasam, H., & Amiri, A. (2018). Natural Convection of Third Grade Non-Newtonian Fluid Flow in a Changeable Semi-permeable Medium Considering the Effects of Variable Heat Source and Magnetic Field. European Journal of Sustainable Development Research, 2(3), 33. https://doi.org/10.20897/ejosdr/2665
Vancouver
Maghsoudi P, Sadeghi S, Rasam H, Amiri A. Natural Convection of Third Grade Non-Newtonian Fluid Flow in a Changeable Semi-permeable Medium Considering the Effects of Variable Heat Source and Magnetic Field. EUR J SUSTAIN DEV RES. 2018;2(3):33. https://doi.org/10.20897/ejosdr/2665
AMA
Maghsoudi P, Sadeghi S, Rasam H, Amiri A. Natural Convection of Third Grade Non-Newtonian Fluid Flow in a Changeable Semi-permeable Medium Considering the Effects of Variable Heat Source and Magnetic Field. EUR J SUSTAIN DEV RES. 2018;2(3), 33. https://doi.org/10.20897/ejosdr/2665
Chicago
Maghsoudi, Peyman, Sadegh Sadeghi, Hamed Rasam, and Ahad Amiri. "Natural Convection of Third Grade Non-Newtonian Fluid Flow in a Changeable Semi-permeable Medium Considering the Effects of Variable Heat Source and Magnetic Field". European Journal of Sustainable Development Research 2018 2 no. 3 (2018): 33. https://doi.org/10.20897/ejosdr/2665
Harvard
Maghsoudi, P., Sadeghi, S., Rasam, H., and Amiri, A. (2018). Natural Convection of Third Grade Non-Newtonian Fluid Flow in a Changeable Semi-permeable Medium Considering the Effects of Variable Heat Source and Magnetic Field. European Journal of Sustainable Development Research, 2(3), 33. https://doi.org/10.20897/ejosdr/2665
MLA
Maghsoudi, Peyman et al. "Natural Convection of Third Grade Non-Newtonian Fluid Flow in a Changeable Semi-permeable Medium Considering the Effects of Variable Heat Source and Magnetic Field". European Journal of Sustainable Development Research, vol. 2, no. 3, 2018, 33. https://doi.org/10.20897/ejosdr/2665

 Full Text (PDF)
Full Text (PDF)