INTRODUCTION

Recently, energy saving is one of the most important and most challenging subjects in different industries like refrigeration systems. So it is important to evaluate and optimize their performance. The increase of energy demand has resulted in development of novel and advanced thermal systems which have lower environmental impacts and higher efficiency (Self et al., 2018). Some refrigeration cycles benefit from ejectors for their proper performance. Ejectors are used as thermo-compressors in refrigeration systems. Though ejectors are used in refrigeration systems due to the simplicity of manufacturing, these vehicles have relatively low efficiency. To improve their performance, operational conditions, as well as geometrical parameters of ejectors, could be assessed.

Refrigeration systems use some refrigerants like R12 and R134a due to their excellent thermodynamic properties. On the other hand, the use of environment-friendly refrigerants has received more attention recently, since the depletion of ozone layer and global warming are increased due to the use of conventional refrigerants (Pandya et al., 2017). For instance, according to the Montreal and Kyoto protocols, due to the destructive effects on the ozone layer, R12 refrigerant should have been phased out until 2010. Also, the use of R134a refrigerant must be reduced because of its high global warming potential (GWP) (Rasti et al., 2012). Within many studies, researchers have shown that the use of environment-friendly refrigerants could be a suitable substitute, and the type of refrigerants will affect the ejector performance as a part of a refrigeration cycle. Besides, previous investigations showed that the geometry of an ejector mixing chamber plays a crucial role in the operation of ejectors. For this purpose, many empirical, analytical and numerical investigations have been performed. Cizungu et al. (2001) investigated an ejector performance using environment-friendly refrigerants R123, R134a, R152a, and R717. The results showed that, for different boiler temperatures, the entrainment ratio and the system efficiency depend on the ejector geometry and the compression ratio. Roman and Hernandez (2011) evaluated the performance of an ejector cooling system using propane, butane, isobutene, R152a, and R134a. It was found that the system which used propane, had the highest coefficient of performance (COP). Varga et al. (2013) numerically investigated a variable area ratio ejector using R600a and R152a refrigerants. As a specific result, they found that for a fixed geometry, the ejector is very sensitive to variations in operating conditions which can have an adverse effect on the ejector performance. Wang et al. (2015) used a thermodynamic model to simulate the ejector by introducing the real properties of refrigerants including R1270, R32, R134a, R125, R115 and carbon dioxide. It was concluded that R1270 has the highest COP at the same operating conditions. Milazzo and Rocchetti (2015) developed a thermodynamic simulation code for the modeling of ejector chillers with steam and other working fluids. They reported that water yields poor results in terms of COP, whereas low GWP fluid HFO1233zd gives good results. Mazelli et al. (2015) within an experimental and computational investigation on a supersonic air ejector, reported that different turbulence models have almost same accuracy in predicting various parameters such as the mass flow rate and the entrainment ratio. It was stated that in general a particular model may not be offered. Del Valle et al. (2014) experimentally studied an R134a ejector refrigeration system using three different ejectors. Results indicated that the stagnation degree of superheating of inflows does not affect the mass ratio for values higher than 10℃\(\ 10\). Also during a computational study (del Valle et al., 2015) they evaluated the effects of real gas model and different turbulence models on flow pattern inside the ejector. In seeking for alternatives refrigerants for the widely used refrigerant R134a, other studies were carried out (Lawrence and Elbel, 2014; Li et al., 2014). Boumaraf et al. (2014) performed an analysis on a constant area mixing model ejector to illuminate the effects of the ejector area ratio and condenser temperature while refrigerants R134a and R1234yf were used as working fluids. The results indicated that, under new conditions, the enhancement of COP for the refrigerant R1234yf was higher than that of R134a. Within another study, Gaurav and Kumar (2016) studied a solar ejector-jet refrigeration system to evaluate the performance of the refrigeration cycle using R1234yf and R134a. It was also reported that performance of the system with R1234yf was higher than R134a. Meng et al. (2016) theoretically appraised the performance of R1234ze, R152a, and mixture of R1234ze and R152a with different ratios in a vapor compression system. As a specific result, it was demonstrated that the cooling capacity of the system increased using R152a and decreased using R1234ze compared with R134a.

To evaluate the effects of geometrical parameters, some other studies have been carried out. Yan et al. (2012) found an optimum convergence angle for the ejector mixing chamber. For the found optimum converging angle, the entrainment ratio was maximum. Wu et al. (2014) numerically evaluated the effects of the length and the convergence angle of an ejector mixing chamber and reported that, these parameters would affect the entrainment ratio significantly. By investigating the effects of various geometrical parameters such as the primary nozzle and the mixing chamber configurations, Lin et al. (2013) obtained the optimum conditions for proper operation of an adjustable ejector. Palacz et al. (2016) used a numerical approach to obtain the optimized configuration of a CO₂ ejector mixing section. Results showed that compared with the baseline design, the mixing section length was greater for the optimized design. Furthermore, within another study Palacz et al. (2017) used computational fluid dynamic approach and genetic algorithm to optimize the performance of a CO₂ refrigeration ejector. They evaluated the nozzle and the mixing section geometry and reported that the system efficiency increased 6%. Recently, Wu et al. (2018) investigated effects of various geometrical parameters such as: NXP, the nozzle outlet diameter and the diameter of the contraction part of the mixing chamber on a steam ejector and concluded that these factors affect the performance of the ejector in term of entrainment ratio significantly.

However, these studies regarding the effects of geometrical parameters such as mixing chamber configurations did not consider the effects of these factors on the ejector critical back pressure or temperature; while the performance of an ejector is described by two important parameters including the entrainment ratio and the critical back pressure. The entrainment ratio is proportional to the system efficiency. On the other hand, the critical point (The corresponding pressure and temperature to this point are called critical back pressure and critical back temperature respectively) is another factor which has a prominent effect on the appropriate operation of an ejector and beyond this point, while the ejector outlet pressure or back pressure is higher than the critical back pressure, the entrainment ratio would be affected adversely by influencing the flow field inside the system. Indeed, the critical point determines the range of appropriate operating pressures or temperatures of the ejector outlet. At these conditions, the ejector would be able to work efficiently. In a refrigeration system, the outlet of an ejector is connected to a condenser. Therefore, the critical point determines the range of operating temperatures or pressures of the condenser at which the entrainment ratio is maximum.

Based on the above-mentioned investigations, one may conclude that choosing a proper refrigerant as the working fluid, especially environment-friendly refrigerants, is very important; because, the thermodynamic properties of refrigerants severely affect the performance of the ejector and the refrigeration system. Also, the geometry of ejector mixing chamber could be a crucial factor in the performance of ejectors.

In this work firstly, experimental data from the study of del Valle et al. (2014) was used to validate the CFD results. They used R134a refrigerant as working fluid. Because of the relatively high geothermal impact of R134a, it has been replaced with two other environment-friendly refrigerants R1234ze(E) and R1234yf with similar thermodynamic properties. Then, the ejector performance and the refrigeration system COP with these fluids have been investigated. In selection of working fluids, some parameters such as ozone depletion potential (ODP) and GWP have been considered. In the second part of this study, effects of the convergence angle of the ejector mixing chamber on the entrainment ratio, the system COP, the fluid flow, and the critical back pressure are obtained.

OPERATING PRINCIPLES OF EJECTOR

Ejector Unit

Figure 1 shows a schematic view of an ejector refrigeration cycle that contains a boiler, a condenser, an evaporator, an ejector, a pump and an expansion device. An ejector is an important component of a refrigeration system that is used as a replacement for a compressor.

 

Figure 1. Schematic of the ejector refrigeration system

 

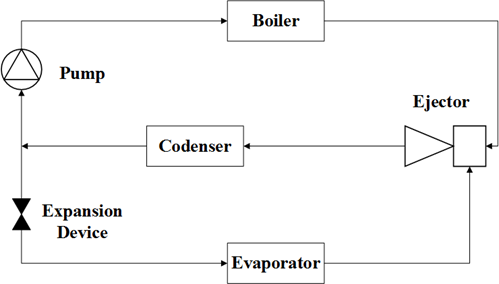
The ejector is composed of two convergent-divergent nozzles to mix two streams that enter through the two inlets and compress the stream of suction flow. Motive or primary flow (the output of the boiler) with high pressure passing through the primary convergent-divergent nozzle expands and reaches supersonic condition and consequently, a low-pressure zone at the nozzle outlet would be created and as a result, the suction or secondary flow (the output of the evaporator) is drawn into the ejector suction chamber. In the mixing chamber, the two streams are mixed creating a supersonic flow. When reaching the diffuser, the mixed flow should adjust to the outlet conditions and consequently, several shocks might be generated. The trend of flow pressure and velocity in an ejector are illustrated qualitatively in Figure 2.

 

Figure 2. The trend of flow pressure and velocity in an ejector

 

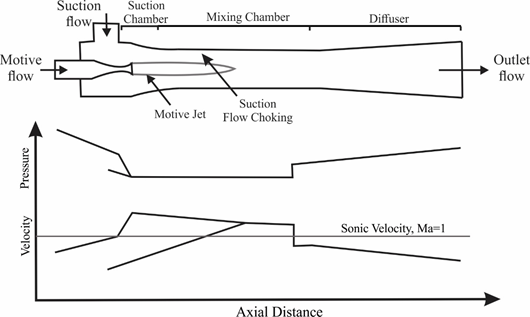
Ejector Performance

The entrainment ratio is a characteristic of the ejector performance and is defined as the mass flow rate ratio of the secondary flow to the primary flow. It is given as:

\[ER = \frac{{\dot{m}}_{s}}{{\dot{m}}_{p}}\]

(1)

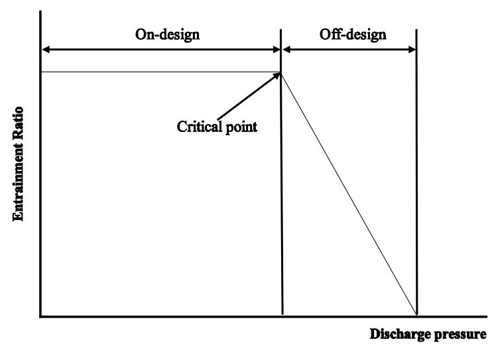
As shown in Figure 3, for any ejector there is a characteristic curve that describes its performance. One important parameter on the curve is the critical point. While the flow inside the mixing chamber of the ejector is supersonic, the ejector is in "on-design" condition and the flow is called "choked". In these conditions, the suction flow rate is independent of the outlet pressure and entrainment ratio is maximum. Otherwise, the ejector is in "off-design" condition whereas suction mass flow rate would depend on the discharge pressure and this is not a desired condition. The pressure or temperature related to the critical point is called "critical back pressure or temperature" in this study.

 

Figure 3. An ejector characteristic curve

 

Working Fluid Selection

Choosing an appropriate refrigerant is very important due to impact on the system efficiency, the size of the system components, safety and environmental concerns (Choi et al., 2013). Table 1, provides the refrigerants used in this work with their physical, environmental and safety features. R134a refrigerant with excellent thermodynamic properties has relatively high GWP that would be a concern in refrigeration applications. Consequently, two other refrigerants including R1234ze(E) and R1234yf with lower GWP compared with R134a are considered in this study. Also, the value of ODP for all of these refrigerants is zero. It is noteworthy that R1234yf and R1234ze(E) have also other positive features of low flammability and non-toxic which make them appropriate candidates for use in refrigeration applications instead of R134a (Meng et al., 2016). Besides, R1234yf has good thermodynamic properties as R134a. Actually, thermodynamic properties of R1234yf are similar to those of R134a. As a consequence, when replacing the R134a by R1234yf, the change of equipment would be minimized (Choi et al., 2013). Furthermore, compared to other working fluids such as CO2 which is a natural refrigerant, the merit of R1234yf is that this refrigerant can be directly charged into conventional refrigeration systems for instead of R134a with only minor modifications (Boumaraf et al., 2014).

In the first and second columns of Table 1, the refrigerant name and chemical formula are shown. The third column contains the refrigerant molecular mass that could influence the ejector size. In the fourth and fifth columns, the critical values of temperature and pressure are indicated. These parameters are related to the higher conditions in which a boiler or generator can operate in a subcritical system (Roman and Hernandez, 2011). By the increase of the critical temperature and pressure, the boiler could experience wider ranges of temperatures and pressures. The sixth column contains the latent heat of vaporization at boiling point. System efficiency will increase by enhancement of the latent heat. Actually, a refrigerant with higher latent heat absorbs more energy in the evaporator. As a consequence, the required mass flow rate, the size of the facility and the pump energy consumption would be decreased (Maizza and Maizza, 2001; Chen et al., 2010). The seventh column illustrates the normal boiling point. As lower the value of this temperature is, the higher pressures in the system will be (Roman and Hernandez, 2011). The type of the fluid is indicated in the eighth column. There are three categories of working fluids: wet fluids, dry fluids, and isentropic fluids. The slope of vapor saturation line in the temperature-entropy diagram is the main difference between these three categories. A wet fluid has a negative slope, a dry fluid has a positive slope and an isentropic fluid has a nearly infinite slope. Finally, the last three columns show the environmental and safety characteristics of the refrigerants (Calm and Hourahan, 2011).

 

Table 1. Properties of selected refrigerants obtained from (Calm and Hourahan 2011). Name Chemical formula Molecular weight (g/mol) Critical temperature (℃) Critical pressure (bar) Latent heat of vaporization at normal boiling point (kJ/kg) Normal Boiling Point (NBP) (℃) Fluid types LFL (%) Safety group GWP R134a CH2FCF3 102.03 101.1 4.059 215.9 -26.5 Wet None A1 1300 R1234ze CHF=CHCF3 114.04 109.37 3.636 195.4 -18.96 Dry 7.6 A2L 6 R134ayf CH2=CFCF3 114.04 94.7 3.382 183.2 -29.49 Dry 6.5 A2L 4

 

CFD AND THERMODYNAMIC MODEL

Numerical Procedure

CFD simulation is performed using commercial CFD software (Fluent). Using finite volume method for discretization, the nonlinear governing equations of turbulent flow are solved in steady state condition. For this purpose, an implicit density based solver is used. The CFD analysis is conducted using a two-dimensional model. In this regard, a 2-D axisymmetric model is employed to take into account the 3-D effects as well as to reduce the mesh size and processing time. A second-order upwind scheme is used to discretize flow variables. The solution is considered to be converged when the relative residuals are below 10^-6 \(10^{- 6}\)for all variables. Pressure inlet and pressure outlet boundary conditions are applied to the inlet and the outlet of the ejector, respectively. Since the input and the output flow velocities of the ejector are very low compared to the flow velocity inside the ejector, there is not much difference between the static pressure and the stagnation pressure at the ejector boundaries. Consequently, the static pressure was considered as the stagnation pressure in boundaries. To simplify the analysis, the ideal gas model is employed to investigate the fluid behavior inside the ejector and all thermo-physical properties are assumed to be constant except density, which is computed from the ideal gas equation. It was proved by researchers that that ideal gas model could provide similar results to a real gas model (Sriveerakul et al., 2007; Wu et al., 2018). Heat transfer through the walls is neglected because the fluid in the ejector has high speed.

Concisely, the following assumptions are made in the numerical procedure:

• The flow is considered to be axisymmetric.

• The flow is considered to follow the ideal gas treatment.

• The flow velocity at boundaries is neglected.

• The heat transfer through ejector walls is neglected.

As it was mentioned earlier, to reduce the processing time, a 2-D model is used instead of 3-D model in the current study.

Governing Equations

General forms of the conservation equations that describe the compressible flow are shown in equations (2)-(4):

\[\frac{\partial\rho}{\partial t} + \frac{\partial(\rho u_{i})}{\partial x_{i}} = 0\]	(2)
\[\frac{\partial(\rho u_{i})}{\partial t} + \frac{\partial}{\partial x_{j}}\left( \rho u_{i}u_{j} \right) = - \frac{\partial P}{\partial x_{i}} + \frac{\partial\tau_{\text{ij}}}{\partial x_{j}}\]	(3)
\[\frac{\partial(\rho E)}{\partial t} + \frac{\partial}{\partial x_{i}}\left( \rho u_{i}E + u_{i}P \right) = \frac{\partial P}{\partial t} + \frac{\partial}{\partial x_{i}}\left( k_{\text{eff}}\frac{\partial T}{\partial x_{i}} \right) + \frac{\partial}{\partial x_{j}}(u_{i}\tau_{\text{ij}})\]	(4)

where ρ, u, P, E, k_eff, τ, and T represent the density, velocity, pressure, total energy, thermal conductivity, stress tensor and temperature respectively. Equations (2-4) represent the conservation of mass, momentum and energy respectively.

Thermodynamic Analysis of the Refrigeration Cycle

The COP is defined as the ratio of the cooling capacity (\({\dot{Q}}_{\text{evaporator}})\)to heat supply to the boiler (\({\dot{Q}}_{\text{boiler}})\)and the required work for the pump (\({\dot{W}}_{\text{pump}}\)). The cooling capacity, required heat for the boiler and the pump work, as the main sources of energy exchanges, are calculated from the equations (5)-(7) as follows:

\[{\dot{Q}}_{\text{evaporator}} = {\dot{m}}_{\text{evaporator}}(h_{\text{eo}} - h_{\text{ei}})\]	(5)
\[{\dot{Q}}_{\text{boiler}} = {\dot{m}}_{\text{boiler}}(h_{\text{bo}} - h_{\text{bi}})\]	(6)
\[{\dot{W}}_{\text{pump}} = {\dot{m}}_{\text{boiler}}(h_{\text{po}} - h_{\text{pi}})\]	(7)

Therefore, the COP is calculated from the equation (8):

\[COP = \frac{{\dot{m}}_{\text{evaporator}}(h_{\text{eo}} - h_{\text{ei}})}{{\dot{m}}_{\text{boiler}}\left( h_{\text{bo}} - h_{\text{bi}} \right) + {\dot{m}}_{\text{boiler}}(h_{\text{po}} - h_{\text{pi}})} = ER\frac{h_{\text{eo}} - h_{\text{ei}}}{h_{\text{bo}} - h_{\text{pi}}}\]

(8)

where \(h_{\text{eo}}\), \(h_{\text{ei}}\), \(h_{\text{bo}}\), \(h_{\text{bi}}\), \(h_{\text{po}}\), \(h_{\text{pi}}\) represent the refrigerant enthalpy at the evaporator outlet, the evaporator inlet, the boiler outlet, the boiler inlet, the pump outlet, and the pump inlet respectively. \({\dot{m}}_{\text{evaporator}}\) and \({\dot{m}}_{\text{boiler}}\) are the mass flow rates of the evaporator and the boiler respectively. Also, \({\dot{Q}}_{\text{evaporator}}\) and \({\dot{Q}}_{\text{boiler}}\) are the heat input to the evaporator and boiler respectively. \({\dot{W}}_{\text{pump}}\) is the pumping power, and the ER represents the ejector entrainment ratio.

The system COP is proportional to the entrainment ratio, which depends on the ejector geometry, operating conditions, refrigerant, and to a ratio of enthalpy differences which depends only on the working fluid.

The following assumptions have been made for the thermodynamic analysis of the refrigeration cycle:

• The streams at the evaporator and the boiler exit are saturated vapor.

• The stream at the condenser exit is saturated liquid.

• The pressure losses are neglected within the stream lines.

• The expansion device is considered to be isenthalpic.

• The pump is considered to work ideally.

Turbulence Modelling

Considering the previous studies like Mazelli et al. (2015), del Valle et al. (2015), Allouche et al. (2014) and Hemidi et al. (2009), one may realize that there is not an exact recommendation for choosing a proper turbulence model but totally, the SST turbulence model and ε-based turbulence models predict parameters such as mass flow rate relatively close to the experimental data; however it is worth to note that, these models provide different predictions for the pressure profile and the shock position.

The k-ε standard model is a widely used model because of being robust, economic and accurate over wide range of turbulent flows. This model is a semi-empirical model. When using this model, it is assumed that the flow is fully turbulent and molecular viscosity effects are negligible. The k-ε RNG model is derived from the instantaneous Navier-Stokes equations, using a mathematical technique called “renormalization group” (RNG) methods. The analytical derivation leads to a model with constants different from those in the standard model, and additional terms and functions in the transport equations for k and ε. This model is known to be more accurate and reliable over wide range of flows than the standard model. The k-ε realizable model is known as promoted version of the standard model. Using this model, the turbulence viscosity is appraised in a different way and a new transport equation for the dissipation rate (ε) has been derived. This model is capable of capturing properly the flows with features of strong streamline curvature, vortices, and rotation. The shear stress transport (SST) k-ω model uses the k-ω formulation in the near-wall region and the k-ε formulation in the far field. The SST model is more accurate and reliable for wide variety of flows including airfoils, transonic shock waves, and adverse pressure gradient flows, compared to other above-mentioned models (Fluent, 2012).

In the present study, four different turbulence models namely k-ω SST, Standard k-ε, Realizable k-ε and k-ε RNG are used to capture the flow behavior. Finally, the SST model which benefits from the combination of k-ω model near walls and inside boundary layer and k-ε model in free stream (Song and Shen, 2017) is used for simulations, since this model predicted the entrainment ratio more accurately compared with the other models.

Ejector Geometry and Grid Generation Procedure

The ejector geometry is chosen from the experimental work of del Valle et al. (2014). Some important dimensions of the studied ejector are demonstrated in Table 2.

 

Table 2. Dimensions of important parts of the employed ejector in this study Geometry Dimension (mm) Throat diameter of primary nozzle 2 Outlet diameter of primary nozzle 3 Inlet diameter of mixing chamber 6.4 Outlet diameter of mixing chamber 4.8 Length of mixing chamber 40 Nozzle exit position 4.37

 

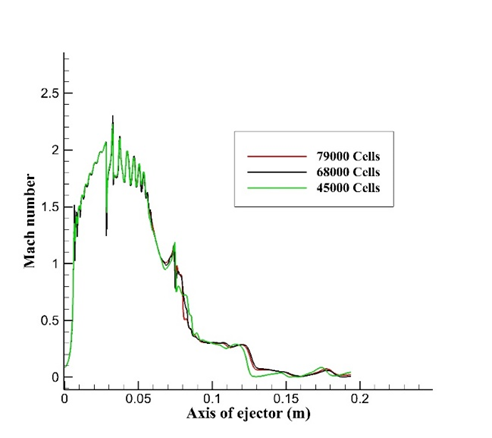
Gambit 2.4.6 is used to generate the required mesh employing structured quadratic control volumes. The considered mesh for the computational domain is shown in Figure 4. In order to ensure that numerical results are independent of the grid resolution, the amount of grid density of 45000, 68000 and 79000 cells are employed for the computational domain. For this purpose, the mesh density is increased in the areas that are anticipated to have sharp velocity gradients and mixing of two streams of motive and suction flows.

 

Figure 4. The considered mesh for the computational domain

 

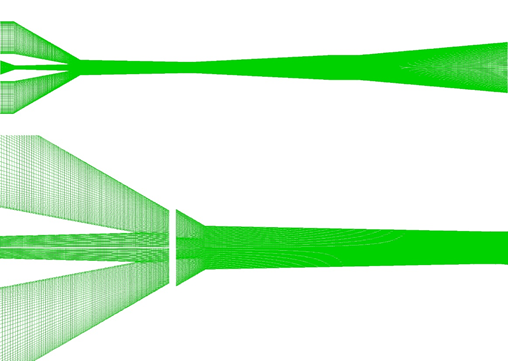
Figure 5 shows the Mach number distribution on the ejector axis for three different cases of meshes. The results in Figure 5 indicate that by increase of the grid resolution beyond a certain value (i.e., 68000 cells) the results of variation of Mach number distribution on the ejector axis would not change considerably.

 

Figure 5. The effects of grid resolution on Mach number distribution on the ejector axis for the case of R134a refrigerant

 

RESULTS

In the current investigation, primarily the numerical results are validated with respect to the experimental results. After validation of numerical results, the effects of the use of R1234ze and R1234yf, as alternatives for R134a, on the ejector entrainment ratio and the system COP are studied. Finally, the effects of the convergence angle of the ejector mixing chamber on the entrainment ratio, the system COP, the flow behavior inside the ejector and consequently on the critical pressure are evaluated.

Validation of CFD Results

The experimental and numerical data from the study of del Valle et al. (2015) is used to validate the obtained CFD results. R134a refrigerant is used as the working fluid in this regard. The saturation temperatures in the form of T_sat\(T_{\text{sat}}\) were employed, instead of the pressure readings, for the ejector inlet and outlet boundary conditions. Moreover a 10℃ superheat is considered at the boiler and the evaporator exit based on the study of del Valle et al. (2015).

The studied operating condition, CFD results and experimental results are presented in Table 3. As shown, the predicted values for entrainment ratio are in good agreement with experimental data and their related calculation error are below 7%.

Table 3. Comparison of the CFD and experimental results Operating temperature (Co) Entrainment ratio Primary flow Entrained flow Obtained from experimental results Obtained from CFD results Error (%) 89 10 0.43 0.41 5.3 89 5 0.36 0.34 6.37 84 10 0.59 0.55 6.8

 

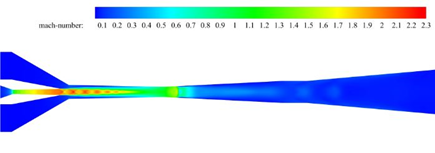
Figure 6, shows the Mach number contour of the ejector while the primary and secondary flows temperatures are 89 and 10 Celsius respectively. It can be seen that a train of compression and expansion waves exist inside the long tapered mixing chamber. Extending from the primary nozzle exit, these waves gradually die down because of the mixing process of two streams of the motive flow and the suction flow. The mixing process continues until the mixed flow reaches the diffuser. Then, at the beginning of the diffuser, a shock wave is generated so that the mixed flow adjusts to the discharge conditions.

 

Figure 6. Mach number contour of the ejector while the motive and suction flow temperatures are 89 and 10 Celsius respectively

 

EJECTOR PERFORMANCE

Effect of Working Fluids

Figure 7 illustrates the comparison of the ejector entrainment ratio for various refrigerants under conditions of boiler temperature of 84.39℃, evaporator temperature of 10℃ and condenser temperature of 26℃.

 

Figure 7. Comparison of the ejector entrainment ratio and the system COP for different refrigerants

 

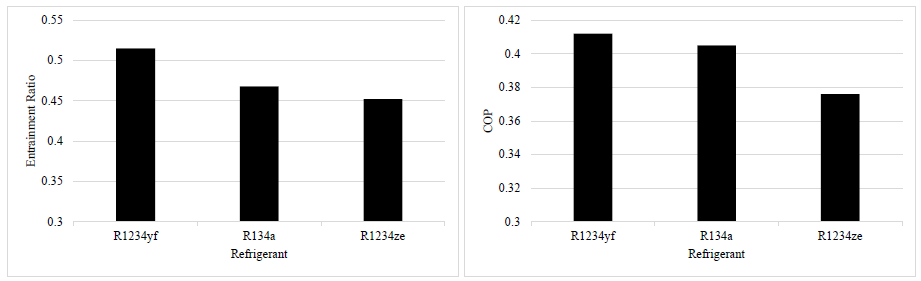
The maximum and minimum entrainment ratios are obtained using R1234yf and R1234ze respectively. Using R1234yf, the entrainment ratio increases about 10% with respect to the R134a. This means using this refrigerant, more mass flow would pass through the evaporator which would result in enhancement of the cooling capacity of the refrigeration system. On the contrary, using R1234ze the entrainment ratio does not increase and the entrainment ratio is 3.4% less than that of R134a.

Table 4 shows the values of entrainment ratios and the corresponding pressure ratios for three refrigerants.

 

Table 4. Obtained entrainment ratio values for three refrigerants and their corresponding pressure ratios of the evaporator to the boiler Refrigerant Pressure ratio of the evaporator to boiler Entrainment Ratio R1234yf 0.159 0.515 R134a 0.144 0.468 R1234ze 0.141 0.452

 

It is worth noting that there is a direct relation between the value of the entrainment ratio and the ratio of pressures of the evaporator to the boiler. For instance, the ratio of the pressure of evaporator to the boiler for R1234yf is higher than that of R134a and R1234ze and the entrainment ratio for this refrigerant is higher than the two other fluids. As a result, it can be concluded that thermodynamic properties of refrigerants have a significant influence on the performance of the system.

The comparison of the system COP for three refrigerants is also illustrated in Figure 7. The results showed that compared with R134a, the system COP increased slightly using R1234yf about 1.7%, while using R1234ze the COP decreased 7%. As it was mentioned, the COP is a function of the entrainment ratio and the ratio of enthalpy differences. Consider two working fluids R1234yf and R134a with the highest COP. Though using R134a, the ratio of enthalpy difference was higher than that of R1234yf, the COP was higher slightly for the refrigerant R1234yf due to the higher entrainment ratio which was obtained by this fluid

Effect of the Boiler Temperature

Figure 8 indicates the effect of the boiler temperature on the ejector entrainment ratio while the secondary flow temperature and the discharge temperature are kept constant at (T_sat\({(T_{\text{sat}})}_{\text{discharge}} = 27\))_Evaporator=10℃ \({(T_{\text{sat}})}_{\text{evaporator}} = 10\)and (T_sat\({(T_{\text{sat}})}_{\text{discharge}} = 27\))_Discharge=26℃ respectively.

 

Figure 8. Effect of the boiler temperature on the ejector entrainment ratio and the system COP for (T_sat)_evaporator=10℃ and (T_sat)_discharge=26℃

 

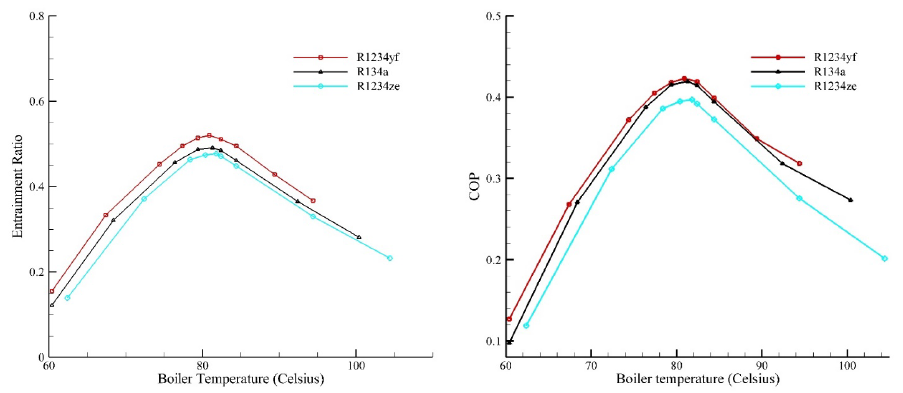
Figure 8 also illustrates that R1234yf has the highest entrainment ratio while the lowest entrainment ratio is obtained by R1234ze. Furthermore, R1234yf has a limited temperature range of operation compared to the other cases due to the lower critical temperature that it has. As a consequence, using this refrigerant (i.e., R1234yf), the boiler could operate in a lower range of temperatures.

As results indicate, for the boiler operating temperature an optimum value was found. At this point, the ejector performance in term of the entrainment ratio is maximum. For lower values of the boiler temperature, the entrainment ratio is low. By the gradual increase of the boiler temperature, the mass flow rate of the motive flow increases. Also, due to the shear stress between two streams of motive flow and suction flow, the mass flow rate of the suction flow increases too. Consequently, the entrainment ratio increases since the suction flow increases more relatively. However, after reaching an optimum value of the boiler temperature, the entrainment ratio decreases. The reason behind this behavior is that by further enhancement of the motive flow temperature, the suction mass flow rate decreases smoothly. The increment of the primary flow temperature leads to a higher angle of expansion in the primary flow jet which leaves the primary nozzle. As a consequence, there will remain a limited zone between the jet and the ejector walls that will lead to entrainment of less secondary flow into the ejector. The above-mentioned factor along with the increase of the primary mass flow rate due to the increment of the boiler temperature result in the reduction of the entrainment ratio.

Figure 9 shows the Mach number contour for different values of boiler temperatures while R134a is used as the working fluid. As indicated, the increase of the primary flow temperature enhances the Mach number. Also, the increase in the pressure and the mass flow rate leads to stronger shocks in the diffuser and results in the movement of shocks to the downstream. One result of this phenomenon is that the critical pressure increases. In ejectors with conical mixing chambers, despite the ejectors with cylindrical mixing chambers, the secondary flow does not reach the sonic condition, although the entrainment ratio is constant and the flow inside the ejector could be called “Double-choked”. In conical mixing chambers, though the secondary flow does not reach sonic condition, the mass flow rate of suction flow is independent of the discharge pressure due to the formation of a shock wave at the end of the mixing chamber. Within the mixing chamber, two streams would be mixed and the mixed flow reaches the sonic condition that contributes to the fact that mass flow rate of inflows and the entrainment ratio remains constant. By elimination of this shock wave for any reason (reduction of primary flow pressure or enhancement of discharge pressure), the entrainment ratio would be decreased significantly which is not a desirable situation.

 

Figure 9. Contours of Mach number for different boiler temperatures at (T_sat)_evaporator=10℃  and (T_sat)_discharge=26℃ . Case (a): (T_sat)_boiler=84.39℃ , Case (b): (T_sat)_boiler=92.39℃ , Case (c): (T_sat)_boiler=100.39℃

 

Figure 8 also shows the effect of increase of the boiler temperature on the system COP for three refrigerants. It was observed that by increasing the boiler temperature, the COP increases. The reason behind this behavior is that by enhancement of the boiler temperature, the entrainment ratio increases. Consequently, the COP increases too. However, after an optimum value of the boiler temperature, the COP decreases, since the entrainment ratio declines continually. Furthermore, it was observed that the rate of decrement of the COP beyond the optimum point has changed. For instance, for the case of R134a, after the boiler temperature of 84 Celsius, the rate of decrease of the COP has decreased. The main reason for this behavior is that after this point, the rate of decrease of the enthalpy difference at the denominator of the equation (8) decreases more relatively. As a result, the COP decreases slightly after this point.

Effect of the Evaporator Temperature

The effect of the evaporator temperature on entrainment ratio for all refrigerants is illustrated in Figure 10 with (T_sat)_Boiler=84.39℃ and (T_sat)_Discharge=26℃.

 

Figure 10. Effect of the evaporator temperature on the ejector entrainment ratio and the system COP for (T_sat)_boiler=84.39℃  and (T_sat)_discharge=26℃ .

 

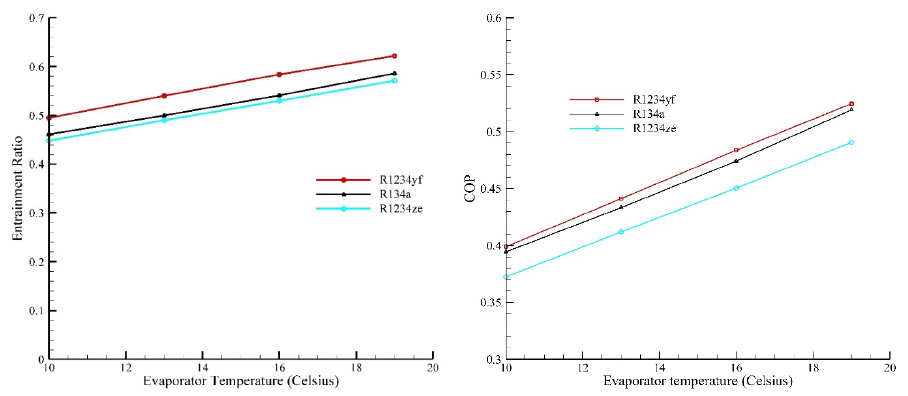
As it can be seen, the increase of the evaporator temperature leads to an increase in entrainment ratio and the variation of entrainment ratio is almost linear. The maximum and minimum values of entrainment ratio are obtained by using R1234yf and R1234ze refrigerants respectively. For the case of R1234yf, the sensitivity of entrainment ratio is 1.4% per Celsius degree of variation of the evaporator temperature. In other words, the amount of variation of entrainment ratio with respect to the one Celsius degree of evaporator temperature is 1.4%.

Actually, the increment of the evaporator temperature increases the pressure difference between the primary nozzle exit and evaporator (i.e., the suction inlet). This pressure difference leads to the enhancement of the suction of the secondary flow and consequently enhances the entrainment ratio.

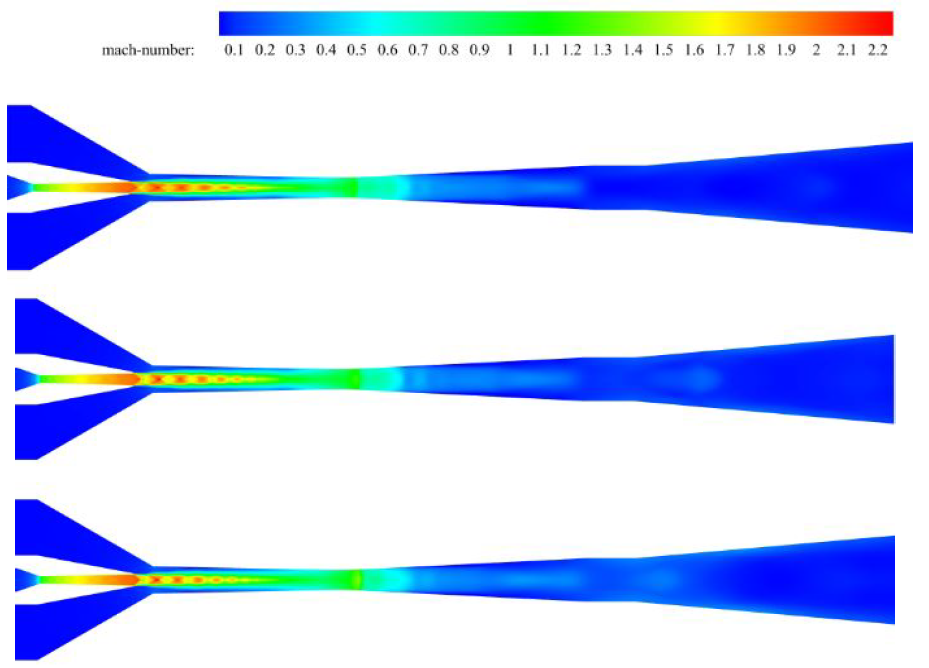
The effect of enhancement of the evaporator temperature is illustrated in Figure 11. It can be seen that by enhancement of the evaporator temperature, similarly to the boiler, stronger shocks are established at the end of the mixing chamber which would result in enhancement of the critical pressure.

 

Figure 11. Effect of the enhancement of the evaporator temperature on Mach number contour of the ejector

 

The effect of the evaporator temperature increment on the system COP is displayed in Figure 10. It was found that by increase of the evaporator temperature, the COP enhances for all refrigerants. According to equation (8), the system COP is a function of the entrainment ratio and the ratio of enthalpy differences. By increment of the evaporator temperature, the entrainment ratio enhances due to the increased pressure difference between the evaporator exit and the primary nozzle exit. The higher the entrainment ratio, the higher the system COP. Actually, as the entrainment ratio increases, more mass flow would pass through the evaporator for a constant mass flow passing thorough the boiler. As a consequence, the evaporator ability in absorbing the heat would increase. Furthermore, by increase of the evaporator temperature, the enthalpy of the refrigerant at the evaporator exit and the ratio of enthalpy differences increase resulting in further enhancement of the system COP.

Effect of the Convergence Angle of the Mixing Chamber

The variation of critical back temperature (Corresponding saturation temperature of critical back pressure at which the entrainment ratio is independent of discharge pressure, but by the further increment of discharge pressure, the entrainment ratio will decrease suddenly) by the convergence angle of the mixing chamber is illustrated in Figure 12. By increasing inlet diameter, the critical temperature decreases continually. To delve deeply into this phenomenon and obtain the reasons behind this, the flow field could be assessed.

 

Figure 12. Effect of the convergence angle of the ejector mixing chamber on the critical back temperature, the ejector entrainment ratio, and the system COP

 

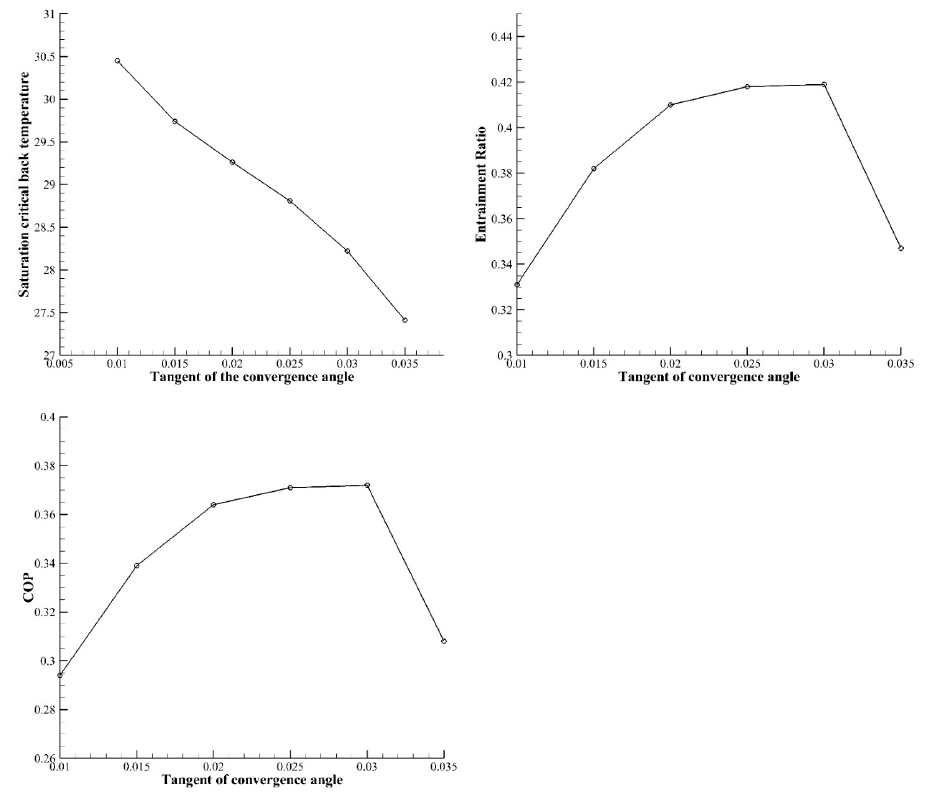
Figure 13 shows the effect of the increase of mixing chamber inlet diameter on Mach number contour while the length and outlet diameter of that are constant and the R134a refrigerant is used as working fluid. These results are obtained while the saturation temperatures of boiler, evaporator, and condenser are 89, 10 and 26 Celsius respectively.

 

Figure 13. Effect of the convergence angle of the ejector mixing chamber on Mach number contour

 

As it is clear in Figure 13, by increase of the inlet diameter, a weaker shock wave is formed at the end of mixing chamber and its position moves toward the ejector. As it was mentioned earlier, formed shock at the end of the mixing chamber plays a crucial role in the performance of the ejector with conical mixing area. The weaker this shock, the lower the critical pressure. As a result, increment of the inlet diameter would result in the reduction of critical pressure of the ejector.

Figure 12 also indicates the variation of the entrainment ratio with converging angle. By gradual increase of the convergence angle, the entrainment ratio enhances. However, after the optimum value of the converging angle, the entrainment ratio declines. By increasing of the mixing chamber inlet diameter, a greater area between the primary jet leaving the primary nozzle and the ejector walls is generated, and the suction of the secondary flow is increased. However, after reaching a specific value of the inlet diameter of the mixing area, the entrainment ratio decreases suddenly because the suction mass flow rate drops significantly. The reason for this behavior is related to the generation of the shock wave at the beginning of the diffuser. As it was explained, in an ejector with long tapered mixing chamber which is working in on-design conditions, the secondary flow does not reach the sonic condition, but the entrainment ratio is independent from the outlet conditions, since the mixed flow reaches supersonic conditions at the beginning of the diffuser which is followed by a shock wave. On the other hand, as it was discussed, by increment of the converging angle a weaker shock wave is established at the diffuser. After reaching a specific value of the inlet diameter, this shock is disappeared. Consequently, the suction mass flow rate and therefore, the entrainment ratio decreases sharply.

According to equation (8), for an ejector working with a refrigerant, the COP is a function of entrainment ratio. The variation of the COP with mixing chamber convergence angle is illustrated in Figure 12. It could be seen that by increasing the convergence angle, the COP enhances. However, beyond a certain value of the convergence angle, the COP decreases. Results showed that by increasing of the converging angle, the COP increases since the entrainment ratio increases. However, by the further increment of the convergence angle, the entrainment ratio and consequently, the COP decreases.

CONCLUSION

The performance of an ejector in a refrigeration cycle has been studied considering different environment-friendly refrigerants and various convergence angles of the mixing chamber in the current study.

In the first part of this study, calculated numerical results were compared and validated with previous related experimental and numerical results of del Valle et al. (2015).

For the next stage of the study, considering the high geothermal impact of R134a refrigerant, (i.e., high GWP of R134a), two other environment-friendly refrigerants namely R1234ze and R1234yf have been used and the ejector performance and the refrigeration system COP with these fluids have been evaluated. Furthermore, the effects of the increase of the boiler and the evaporator temperature on the ejector performance and the flow behavior were studied.

In the final stage of this research, the effect of increase of the mixing chamber convergence angle on the entrainment ratio, the system COP, the critical back temperature and the flow field was assessed. The main conclusions are provided as follows:

Among all refrigerants investigated in this study, the maximum value of the entrainment ratio was obtained with R1234yf. Using this refrigerant, the entrainment ratio increased 10% compared with R134a. On the contrary, using R1234ze the entrainment ratio decreased 3.4% with respect to the R134a. It was observed that there is a direct relation between the pressure ratio values of the evaporator to the boiler for each refrigerant. The higher this ratio for every refrigerant, the higher the entrainment ratio. Furthermore, the results indicated that using refrigerant R1234yf the system COP increased 1.7% compared with R134a. On the other hand, the COP decreased 7% with R1234ze compared to R134a. According to the obtained results, refrigerant R1234yf would be an appropriate alternative for R134a.

Numerical results showed that there is an optimum value for the boiler temperature. For the optimum boiler temperature, the entrainment ratio and COP is maximum. Beyond the optimum point, the entrainment ratio and the COP decrease. However, the increase of the evaporator temperature led to enhancement of the entrainment ratio. The sensitivity of change of the entrainment ratio to the enhancement of the evaporator temperature was 1.4%. This means, by one Celsius enhancement of the evaporator temperature, the entrainment ratio increased 1.4%.

Finally, an optimum convergence angle for the ejector mixing chamber was found. By gradual increase of this angle, the entrainment ratio and the system COP increase. However, beyond this optimum value, a reverse trend is observed. Increasing the converging angle affected the flow field inside the ejector. By the increasing of this angle, a weaker shock was established at the end of the mixing chamber which has a significant role in the proper performance of the ejector. The numerical results showed that by the increase of the convergence angle, the critical back temperature decreased since, in the long tapered mixing chamber, the critical back temperature is dependent of the formed shock at the beginning of the diffuser.

As numerical results of the current study indicated, the use of environment-friendly refrigerants such as R1234yf, as replacements for the the refrigerant R134a with too much GWP, could improve the refrigeration system COP. However, it is suggested that the performance of refrigeration systems by using other environment-friendly refrigerants be studied so as to introduce other promising working fluids for use in industrial applications.

NOMENCLATURE

E	Total energy
\({\dot{m}}_{p}\)	Mass flow rate of primary flow
\({\dot{m}}_{s}\)	Mass flow rate of secondary flow
\(k_{\text{eff}}\)	Thermal conductivity
P	Pressure
T	Temperature
u	Velocity
Greek letters
ρ	Density
τ	Stress Tensor
Abbreviation
CFD	Computational fluid dynamics
COP	Coefficient of performance
ER	Entrainment ratio
GWP	Global warming potential
LFL	Lower flammability limit (% by volume in air)
NBP	Normal boiling point
NXP	Nozzle exit position
ODP	Ozone depletion potential
Subscripts
i,j	Generic space coordinates
sat	Saturation