INTRODUCTION

Consumers are beginning to demand products that are eco-friendly over their life cycles (Collins, 2011). Accordingly, a case is proposed and analyzed here for a line of milk products having a low carbon-footprint product. A key feature is that all processes in the production are powered by net-zero carbon emission energy sources. Dairy farmers producing milk could be required in the future to operate using such energy sources, and one option is to use bio-fuel produced from farm waste, which can be considered a net-zero carbon emission energy source (Loo and Koppejan, 2010). Thermodynamic analysis and optimization of an anaerobic treatment system for whey is presented (Spachos and Stamatis, 2011). In this study, performance investigations weere conducted based on exergy and economic analyses of an anaerobic treatment system of whey and it was concluded that the anaerobic treatment system is a sustainable investment. The impact of food production processes in terms of energy utilization, carbon dioxide emissions and exergy loss in a flavored yogurt production process is investigated (Sorguven and Ozilgen, 2012). The work also identified the direction for the development of new technology in food processing to decrease waste of energy and carbon dioxide emissions. A thermodynamic analysis of a milk pasteurization process assisted by geothermal energy is investigated (Yildirim and Genc, 2015). It was found that highest exergy destruction rate is in the absorber of the vapor absorption cycle. A comprehensive exergy analysis of an industrial-scale yogurt production plant is reported (Jokandan et al., 2015). They noted that the components with high exergy destruction rates are as follows: boiler and air compressor combination of the steam generator, and the ice-water and agitator combination of the refrigeration system. The application of exergy analysis to the dairy industry is reported (Soufiyan and Aghbashlo, 2017). A case study for a yogurt drink production plant is reported. The investigations clearly demonstrated the effectiveness of exergy analysis for determining irreversibilities and losses occurring in a dairy processing plants in order to improve their performance. A comprehensive exergetic performance analysis of an ice-cream manufacturing plant to identify the locations of thermodynamic inefficiencies is conducted (Dowlati et al., 2017). A detailed exergy analysis of an industrial-scale ultrafiltrated cheese production plant based on actual operational data is conducted (Nasiri et al., 2017) in order to provide insights into the performance of the whole plant and its main subcomponents. The study also stressed the role of exergy analysis in performance improvement. The performance of a milk powder production system based on energy and exergy analyses is investigated (Yildirim and Genc, 2017), and observed that greatest the exergy destruction occurs in the evaporator.

In this study, an exergy analysis is performed for various configurations of an integrated multi-generational system which has previously been assessed with an energy analysis (Cuomo et al., 2018). System configurations that can satisfy the energy demands of various farm sizes are considered. We consider the integration of an ammonia based organic Rankine cycle (ORC) to generate power from the exhaust gas exiting the absorption cooling system (ARS) heat exchanger to generate additional electrical power. Sources of exergy destruction, are identified for the biogas-fueled micro gas turbine (MGT) arrangement with heat recovery, and for its components.

Due to the nature of the problem several constraints are placed on the system design:

1. The energy demand of the farm must come directly from the biomass energy generation system. This implies only electricity generated by the unit in excess of the farm’s own electricity requirements can be sold to the grid, as the electricity used to run the farm operation must be 100% from a carbon-neutral source.

2. All of the farm’s current energy demand (Table 1) must be met via the system.

The research reported here focuses on an exergy analysis of the system to meet the needs of different sized Ontario dairy farms considering the constraints. The objective of this work is to investigate the exergy efficiencies of various farm sizes with system configurations that meet the required electricity, and cooling loads. Engineering Equation Solver (EES) software is used to assess the second law performance of several system configurations that meet the energy demand for each farm size.

 

Table 1. Energy demands for selected farm sizes Farm size [cows] Total electricity demand [kW] Electricity demand without milk cooling electrical load [kW] Thermal cooling demand [kW cooling] # of 50 kW ARS Units to meet cooling load 250 28.75 22.7 13.6 1 500 57.5 45.4 27.2 1 1000 115 90.9 54.3 2 1500 172.5 136.3 81.5 2 2000 230 181.7 108.7 3 4000 460 363.4 217.4 5 6000 690 545.1 326.0 7

 

BACKGROUND

This investigation extends with exergy analysis, an energy analysis of an integrated multi-generation energy system for a dairy farm performed previously by the authors (Cuomo et al., 2018). In that study it was found that micro gas turbines could be effectively utilized to meet the electrical and cooling demands of dairy farms in Ontario, Canada, for farms of various sizes, based on the typical electricity use of an Ontario dairy farm (Clarke and House, 2010). The electricity and cooling demands for various Ontario farm sizes are listed in Table 1.

With the electricity and cooling demand of the dairy farm specified, appropriate MGTs and quantities of ARS units are selected to meet the electrical and cooling load requirements for the various farm sizes identified in Table 1.

The MGT modules selected for this particular study are manufactured by Turbec and Capstone. The capacities along with exhaust temperature, and exhaust flow rate for each of the MGT modules are listed in Table 2.

 

Table 2. Turbine configurations considered and technical specifications of MGT modules (Capstone Turbine Corporation, 2012; Turbec, 2012) Manufacturer Turbine model configuration Capacity (kW) Exhaust temperature (°C) Exhaust flow rate (kg s-1) Turbec T100CHP 100 270 0.80 Capstone 2 X C65 130 309 0.98 Capstone 3 X C65 195 309 1.47 Capstone C200 200 280 1.30 Capstone 4 X C65 260 309 1.96 Capstone C400 400 280 2.60 Capstone C600 600 280 4.00 Capstone C800 800 280 5.30 Capstone C1000 1000 280 6.70

 

Figure 1. System layout of topping and bottoming cycles with ORC and ARS subsystems

 

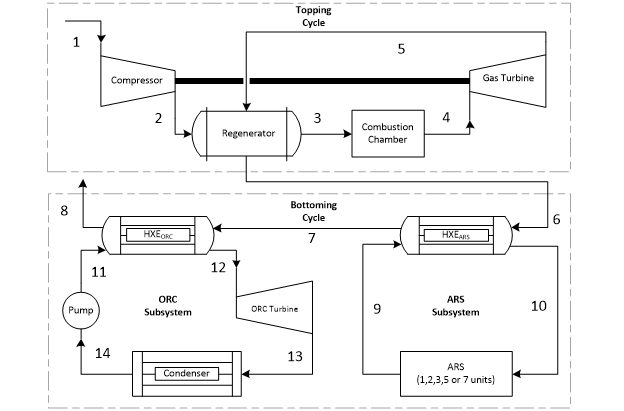
SYSTEM MODELLING

The system and its subsystems are modelled thermodynamically using EES and Excel software. The ambient conditions (selected to be the conditions of the dead state) are taken to be 25°C and 101 kPa. General assumptions follow, while subsystem specific assumptions are listed at the beginning of the corresponding sections:

1. Operation is at steady state.

2. Ideal gas models are applicable.

3. Electromechanical conversion losses are negligible.

4. Changes in kinetic and potential energy are negligible.

A general energy rate balance, which can be applied to each system component, can be written as:

\[{\dot{Q}}_{\text{in}} + {\dot{W}}_{\text{in}} + \sum_{\text{in}}^{}{\dot{m}h} = {\dot{Q}}_{\text{out}} + {\dot{W}}_{\text{out}} + \sum_{\text{out}}^{}{\dot{m}h}\]

(1)

where \(\dot{Q}\) and \(\dot{W}\) denote the heat and electrical work rates respectively, while \(\dot{m}\) and \(h\) are the mass flow rate and specific enthalpy of the working fluid respectively.

A general exergy rate balance, also applicable to each component, can be expressed as follows:

\[\left( 1 - \frac{T_{0}}{T_{b}} \right){\dot{Q}}_{\text{in}} + {\dot{W}}_{\text{in}} + \sum_{\text{in}}^{}\dot{m}ex = \left( 1 - \frac{T_{0}}{T_{b}} \right){\dot{Q}}_{\text{out}} + {\dot{W}}_{\text{out}} + \sum_{\text{out}}^{}\dot{m}ex + \dot{E}x_{d}\]

(2)

where \(T_{0}\) and \(T_{b}\) are the dead state and boundary temperatures respectively, \(\dot{E}x_{d}\) is the exergy destruction rate and \(\text{ex}\) is the specific exergy, defined as:

\[ex = \left( h - h_{0} \right) - T_{0}\left( s - s_{0} \right)\]

(3)

Here, \(h\) and \(s\) are the specific enthalpy and entropy of the working fluid at the actual state with the dead state being represented by \(s_{0}\) and \(h_{0}\) respectively.

Topping Cycle Model

The MGTs were modelled thermodynamically with EES utilizing manufacturer technical specifications, including operating pressures, fuel flow rate, electrical efficiency, exhaust gas flow rate, exhaust temperature, and turbine inlet temperature (Capstone Turbine Corporation, 2012; Turbec, 2012).

 

Table 3. System State Parameters State point Fluid T [°C] Description P [kPa] Notes 1 Air 25 Ambient conditions 101 Intake drawing at atmospheric pressure 2 Air Variable Calculated by model 552 Outlet of compressor, from technical specifications* 3 Air Variable Calculated by model 552 4 Combustion gases 950 Specified by technical specifications of turbine* 552 5 Combustion gases Variable Calculated by model 101 Exhaust at atmospheric pressure 6 Exhaust gas† Variable Set by turbine exhaust conditions 101 7 Exhaust gas† Variable Calculated by model, depends on # of ARS units 101 8 Exhaust gas† 150 To prevent component damage 101 9 Water 105 Required inlet water temp. for ARS* 169 ARS water pressure** 10 Water 115 Specified water outlet temp. for ARS* 169 11 Ammonia 45.6 Calculated by model 3830 Recommended operating pressures for an optimized ammonia based ORC** 12 Ammonia 77 Required inlet ORC turbine inlet temperature** 3830 13 Ammonia 45 Recommended condensation temperature*** 1780 14 Ammonia 45 Recommended condensation temperature*** 1780 †Modelled as air *Data from (Capstone Turbine Corporation, 2012; Turbec, 2012) **Data from (SolarNext, 2008) ***Source reference (Hettiarachchia et al., 2006)

 

In order to model the turbine modules according to the given specifications, the effectiveness of the regenerator as well as the isentropic efficiencies of the compressor and turbine are required. The effectiveness of the regenerator is taken to be 84%, and the turbine and compressor isentropic efficiencies are both taken to be 72%.

The compressor increases the temperature and the pressure of the air, which is heated as it enters the regenerator. The inlet stream to the regenerator is heated by the hot flue gases from the turbine exhaust, which enter the opposite end of the regenerator, in a counter flow configuration. The compressed air reaches the maximum cycle temperature with the firing of biogas in the combustion chamber. The hot combustion gases then expand through the turbine; the turbine shaft is connected to an electrical generator. The high temperature exhaust gases pass through the regenerator to provide preheating to the high pressure stream before being released to the atmosphere.

Assumptions regarding modelling of the topping cycle follow:

1. The compressor, combustion chamber and turbine are adiabatic.

2. All components except the compressor and turbine have negligible pressure drops.

3. Fuel entering the combustion chamber only contains chemical energy and exergy.

4. The specific heat ratio “k” is fixed at 1.4.

The work rate input to the compressor is:

\[\begin{matrix} {\dot{W}}_{MGT,COMP} = {\dot{m}}_{A}\left( h_{2} - h_{1} \right) & \lbrack kW\rbrack \\ \end{matrix}\]

(4)

The heat loss rate of the regenerator is:

\[\begin{matrix} {\dot{Q}}_{LOSS,REGEN} = {\dot{m}}_{A}\left( h_{2} - h_{3} \right) - {\dot{m}}_{\text{gas}}\left( h_{5} - h_{6} \right) & \lbrack kW\rbrack \\ \end{matrix}\]

(5)

The heat input rate to the combustion chambers is:

\[\begin{matrix} {\dot{Q}}_{\text{CC}} = {\dot{m}}_{\text{gas}}h_{4} - {\dot{m}}_{A}h_{3} - {\dot{m}}_{f}h_{f} & \lbrack kW\rbrack \\ \end{matrix}\]

(6)

The work rate produced by the turbine is:

\[\begin{matrix} {\dot{W}}_{MGT,TURB} = {\dot{m}}_{\text{gas}}\left( h_{4} - h_{5} \right) & \lbrack kW\rbrack \\ \end{matrix}\]

(7)

Combustion Modelling

Using the given technical specifications provided by the manufacturer, the parameters of each component are analyzed. The heat input required by the module can be expressed as:

\[\begin{matrix} {\dot{Q}}_{\text{CC}} = {\dot{m}}_{f} \bullet q_{\text{LHV}} & \lbrack kW\rbrack \\ \end{matrix}\]

(8)

where \({\dot{Q}}_{\text{cc}}\) is the energy requirement of the combustion chamber, \({\dot{m}}_{\text{fuel}}\) is the mass flow rate of fuel, and \(q_{\text{LHV}}\) is the lower heating value of biogas, which is taken to be 22 000 kJ kg^-1 (Loo and Koppejan, 2010).

A mass rate balance for the combustion chamber yields:

\[\begin{matrix} {\dot{m}}_{\text{gas}} = {\dot{m}}_{A} + {\dot{m}}_{f} & \lbrack kg\ s^{- 1}\rbrack \\ \end{matrix}\]

(9)

The biogas for this study is taken to be a mixture of 60% methane, 35% carbon dioxide and 5% nitrogen. The biogas and its combustion are modelled as follows:

\[aCH_{4} + bCO_{2} + cN_{2} + d(O_{2} + 3.76N_{2}) \rightarrow eH_{2}O + fCO_{2} + gN_{2} + hO_{2}\]

(10)

Equating coefficients utilizing the air fuel ratio yields:

\[a = 0.6\]

\[b = 0.35\]

\[c = 0.05\]

\[d = m_{\text{BG}} \bullet AF_{\text{BG}} \bullet \frac{1}{M_{A}}\]

\(e = 2a\)

\[f = a + b\]

\[g = c + 3.76d\]

\[h = b + d - \frac{e}{2} - f\]

where \(AF_{\text{BG}}\) is the air-fuel ratio of the biogas.

Physical and Chemical Exergy

The physical exergy of a flow is described earlier (equation 3), but chemical exergy also must be considered to analyze the fuel and exhaust combustion gases.

The total exergy into the system is the exergy of the fuel entering the combustion chamber. The fuel is assumed to enter the combustion chamber at ambient conditions, and thus only to have chemical exergy. Thus,

\[\begin{matrix} {\dot{\text{EX}}}_{f} = {\dot{m}}_{f} \bullet e_{f}^{\text{ch}} & \lbrack kW\rbrack \\ \end{matrix}\]

(11)

where the chemical exergy rate is determined based on the product of the specific chemical exergy and mass flow rate of the fuel. The specific chemical exergy of the biogas is determined based on its composition:

\[\begin{matrix} e_{f}^{\text{ch}} = \ a \bullet e_{CH4}^{\text{ch}} + b{\bullet e}_{CO2}^{\text{ch}} + c{\bullet e}_{N2}^{\text{ch}} & \lbrack kJ\ kg^{- 1}\rbrack \\ \end{matrix}\]

(12)

where \(a\), \(b\), and \(c\) are the combustion coefficients of the biogas. The chemical exergy of selected gaseous constituents is presented in Table 4.

 

Table 4. Molar mass and chemical exergy of common constituents of combustion gases (Moran et al., 2018) Compound Molar mass, M (kg kmol-1) Chemical exergy, \({\overline{\mathbf{e}}}_{\mathbf{i}}^{\mathbf{\text{ch}}}\) (kJ kmol-1) Chemical exergy, \(\mathbf{e}_{\mathbf{i}}^{\mathbf{\text{ch}}}\) (kJ kg-1) \[\text{CH}_{4}(g)\] 16.04 831650 51838.00 \[H_{2}O(g)\] 18.02 9500 527.33 \[CO_{2}(g)\] 44.01 19870 451.49 \[N_{2}(g)\] 28.01 720 25.70 \[O_{2}(g)\] 32.00 3970 124.06

 

The exergy flow rate of the product gases is evaluated as follows:

\[\begin{matrix} {\dot{\text{EX}}}_{P} = {\dot{m}}_{\text{gas}} \bullet ex_{P} & \lbrack kW\rbrack \\ \end{matrix}\]

(13)

where the total specific exergy of the products is a summation of the contributions of the exhaust constituents and accounts for both physical and chemical exergy of each constituent, that is

\[\begin{matrix} ex_{p} = \sum_{i = 1}^{n}{n_{i}\left\lbrack \left( {\overline{h}}_{i} - {\overline{h}}_{0} \right) - T_{0}\left( {\overline{s}}_{i} - {\overline{s}}_{0} \right) + e_{i}^{\text{ch}} \right\rbrack} & \lbrack kJ\ \text{kg}^{- 1}\rbrack \\ \end{matrix}\]

(14)

The Shomate equations are utilized to find the change in molar specific exergy and molar specific entropy from the ambient conditions (NIST, 2012). The Shomate equations follow:

\[\begin{matrix} \overline{h} - {\overline{h}}_{0} = A*T + B*\frac{T^{2}}{2} + C*\frac{T^{3}}{3} + D*\frac{T^{4}}{4} - E*\frac{1}{T} + F - H & \lbrack kJ\ \text{mol}^{- 1}\rbrack \\ \end{matrix}\]

\[\begin{matrix} \overline{s} = A*\ln\left( T \right) + B*T + C*\frac{T^{2}}{2} + D*\frac{T^{3}}{3} - E*\frac{1}{2T^{2}} + G & \lbrack kJ\ \text{kmol}^{- 1}\rbrack \\ \end{matrix}\]

Here, the temperature \(T\) is 1/1000 of the specified temperature in Kelvin and \(A\), \(B\), \(C\), \(D\), \(E\), \(F\), \(G\), \(H\) are Shomate constants for specific compounds. Values of these constants for the product gas constituents are given in Table 5.

 

Table 5. Shomate equation constants for chemical compounds (NIST, 2012), and reference entropy values (Moran et al., 2018) Compound \[{\overline{\mathbf{s}}}_{\mathbf{0}}\] (kJ kmol-1 K-1) A B C D E F G H \[H_{2}O(g)\] 188.720 30.09200 6.832514 6.793435 -2.534480 0.082139 -250.8810 223.3967 -241.8264 \[CO_{2}(g)\] 213.685 58.16639 2.720074 -0.492289 0.038844 -6.447293 -425.9186 263.6125 -393.5224 \[N_{2}(g)\] 191.502 19.50583 19.88705 -8.598535 1.369784 0.527601 -4.935202 212.3900 0.0 \[O_{2}(g)\] 205.033 30.03235 8.772972 -3.988133 0.788313 -0.741599 -11.32468 236.1663 0.0

 

Bottoming Cycle Model

An EES model for the bottoming cycle was developed to assess how the subsystems behave for various configurations, with different heat inputs from the various micro turbine exhaust streams. The number of ARS units required to meet the cooling load can be varied in the model, allowing determination of how much energy can be recovered after the ARS units for additional electricity generation with the considered ORC.

Fluid properties in the system are determined using EES fluid property information. The state point properties of the bottoming cycle are listed in Table 3.

Additional assumptions regarding modelling of the bottoming cycle follow:

1. All system components are adiabatic and, except for the pump and turbine, have negligible pressure drops.

2. The exhaust gas is modelled as air.

3. Turbine and pump isentropic efficiencies within the ORC are 89%.

4. Heat exchangers are 100% efficient.

5. The ARS heat exchanger is modelled as a single heat exchanger regardless of the number of ARS units employed. Thus, it is assumed the sum of all the water flows required by the ARS units pass through the heat exchanger, are heated to the required temperature, and then branched off to n smaller streams feeding n ARS units.

Operational constraints on the system parameters include the following:

1. The temperature of the exhaust gas leaving the system (state 8) is set at 150°C to avoid water vapor condensation and formation of corrosive liquids that may damage components.

2. The ARS subsystem consists of \(n_{\text{ARS}}\) Chillii ACC50 ARS units for a given configuration. If the available energy content of the exhaust gas stream is insufficient to power all \(n_{\text{ARS}}\) ARS units for a given configuration, the configuration is considered unusable.

3. All farms can produce enough manure to generate the required quantity of biogas to run all considered turbines continuously throughout the year.

Organic Rankine Cycle

We can be write the work output rate of the ORC turbine as

\[\begin{matrix} {\dot{W}}_{ORC,TURB} = \ {\dot{m}}_{\text{ORC}}\left( h_{12} - h_{13} \right) & \lbrack kW\rbrack \\ \end{matrix}\]

(15)

the work input rate to the pump as

\[\begin{matrix} {\dot{W}}_{ORC,PUMP} = \ {\dot{m}}_{\text{ORC}}\left( h_{11} - h_{14} \right) & \lbrack kW\rbrack \\ \end{matrix}\]

(16)

the energy extraction rate by the ORC from the exhaust gas as

\[\begin{matrix} {\dot{Q}}_{ORC,HX} = \ {\dot{m}}_{\text{ORC}}\left( h_{12} - h_{11} \right) & \lbrack kW\rbrack \\ \end{matrix}\]

(17)

the energy rejection rate from the ORC condenser as

\[\begin{matrix} {\dot{Q}}_{ORC,COND} = \ {\dot{m}}_{\text{ORC}}\left( h_{13} - h_{14} \right) & \lbrack kW\rbrack \\ \end{matrix}\]

(18)

and the net electrical work output rate from the ORC as

\[\begin{matrix} {\dot{W}}_{ORC,NET} = \ {\dot{W}}_{ORC,TURB} - \ {\dot{W}}_{ORC,PUMP} & \lbrack kW\rbrack \\ \end{matrix}\]

(19)

Absorption Refrigerator

The energy extraction rate by the ARS from the exhaust gas can be expressed as

\[\begin{matrix} {\dot{Q}}_{\text{ARS}} = {\dot{m}}_{\text{ARS}}\left( h_{10} - h_{9} \right) & \lbrack kW\rbrack \\ \end{matrix}\]

(20)

while the mass flow rate of water in the ARS subsystem is:

\[\begin{matrix} {\dot{m}}_{\text{ARS}} = 2.08 \times n_{\text{ARS}} & \lbrack\text{kg}s^{- 1}\rbrack \\ \end{matrix}\]

(21)

where \(n_{\text{ARS}}\) is the number of 50 kW ACC50 ARS units in a considered configuration.

ENERGY ANALYSIS AND RESULTS

The energy (first law) efficiency for the MGT module can be expressed as:

\[\eta_{TC,I} = \frac{{\dot{W}}_{MGT,NET}}{{\dot{Q}}_{\text{CC}}}\]

where the net work output of the MGT module is

\[\begin{matrix} {\dot{W}}_{MGT,NET} = {\dot{W}}_{MGT,TURB} - {\dot{W}}_{MGT,COMP} & \lbrack\text{kW}\rbrack \\ \end{matrix}\]

(22)

The energy efficiency of the bottoming cycle can be written as

\[\eta_{BC,I} = \ \frac{{\dot{W}}_{ORC,NET} + \ {\dot{Q}}_{\text{cool}}}{{\dot{m}}_{\text{gas}}\left( h_{6} - h_{8} \right) + 3n_{\text{ARS}}}\]

(23)

and the energy efficiency of the overall system as

\[\eta_{\text{sys}} = \frac{{\dot{W}}_{MGT,NET} + {\dot{W}}_{ORC,NET} + {\dot{Q}}_{\text{cool}}}{{\dot{Q}}_{\text{CC}} + 3n_{\text{ARS}}}\]

(24)

Topping Cycle

The exergy efficiency of the MGT modules can be expressed as:

\[\eta_{TC,II} = \frac{{\dot{W}}_{MGT,NET}}{{\dot{\text{EX}}}_{f}}\]

(25)

The energy and exergy efficiencies of the different turbine modules are found to be similar, with the exception of the smaller capacity 65 kW module, as seen in Figure 2. The increased flow rate of fuel required for the 65 kW modules is the main contributor to the reduction in energy and exergy efficiencies. The energy efficiencies and fuel flow rates of the MGTs are from manufacturer technical specifications.

 

Figure 2. Comparison of exergy and energy efficiencies of MGT modules using biogas

 

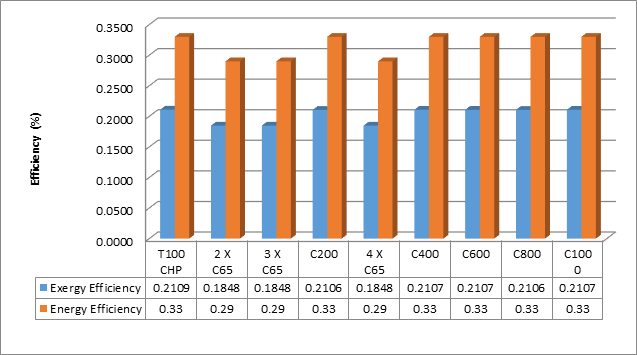
The overall energy and exergy efficiencies of the system give a high level perspective, but a component analysis is required to understand the breakdown of losses for the system. A more detailed analysis is performed on the 1000 kW unit. Exergy rate balances for each of the MGT components are now provided.

Compressor:

\[{\dot{m}}_{A}ex_{1} + {\dot{W}}_{\text{comp}} = {\dot{m}}_{A}ex_{2} + {\dot{\text{Ex}}}_{D,comp}\]

(26)

Regenerator:

\[{\dot{m}}_{A}ex_{2} + {\dot{m}}_{\text{gas}}ex_{5} = {\dot{m}}_{A}ex_{3} + {\dot{m}}_{\text{gas}}ex_{6} + {\dot{Q}}_{\text{loss}}\left( 1 - \frac{T_{o}}{T_{b}} \right) + {\dot{\text{Ex}}}_{D,regen}\]

(27)

Combustion chamber:

\[{\dot{m}}_{A}ex_{3} + {\dot{\text{EX}}}_{f} = {\dot{m}}_{\text{gas}}ex_{4} + {\dot{\text{Ex}}}_{D,CC}\]

(28)

Turbine:

\[{\dot{m}}_{A}ex_{3} + {\dot{\text{EX}}}_{f} = {\dot{m}}_{\text{gas}}ex_{4} + {\dot{\text{Ex}}}_{D,CC}\]

(29)

The exergy analysis locates the largest sources of loss within the system. The largest destruction of exergy within the MGT system is associated with the combustion chamber. Large exergy destructions within a component identify the location and cause (e.g., friction, mixing, expansion, compression, chemical reaction) of the irreversibilities.

Figure 3 shows the exergy destructions of the system components, and the product exergy output for the bottoming cycle. A breakdown by component of the total exergy destroyed is shown for the system in Figure 4.

 

Figure 3. Exergy destruction of the components within the C1000 MGT unit

 

Figure 4. Contribution of exergy destruction within Capstone C1000 MGT system components

 

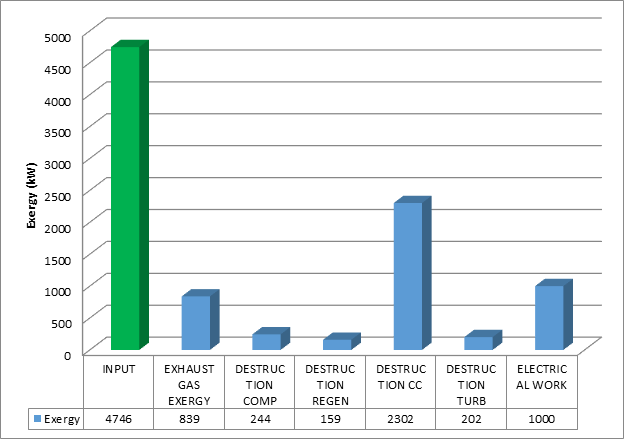
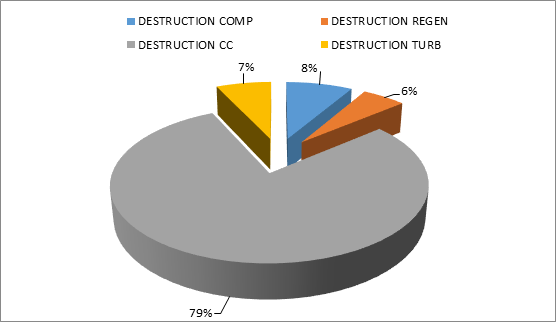
Bottoming Cycle

The exergy (second law) efficiency of the bottoming cycle can be expressed as:

\[\eta_{BC,II} = \ \frac{{\dot{W}}_{ORC,NET} + {\dot{Q}}_{\text{cool}}\left( 1 - \frac{T_{0}}{T_{\text{BC}}} \right)}{{\dot{m}}_{\text{gas}}\left( \text{ex}_{6} - \text{ex}_{8} \right) + 3n_{\text{ARS}}}\]

(30)

For the 1000 kW turbine exhaust, the exergy content of the exhaust gas modelled as combustion products and as air using EES property data are listed in Table 6.

 

Table 6. Exhaust exergy content for two fluid models Cooling configuration (exhaust location) Exhaust stream temperature [C] Exhaust exergy rate (combustion product model) [kW] Exhaust exergy rate (air standard model) [kW] Turbine exhaust 280 839 479 1 ARS exhaust 267 799 439 2 ARS exhaust 255 760 400 3 ARS exhaust 242 722 363 5 ARS exhaust 216 650 291 7 ARS exhaust 191 584 225 Exhaust to Atmosphere 150 492 134

 

Exergy balances for the bottoming cycle components are given below.

Absorption refrigeration heat exchanger:

\[{\dot{m}}_{\text{gas}}ex_{6} + {\dot{m}}_{\text{ARS}}ex_{9} = {\dot{m}}_{\text{gas}}ex_{7} + {\dot{m}}_{\text{ARS}}ex_{10} + {\dot{\text{Ex}}}_{D,ARS}\]

(31)

Absorption refrigeration internal:

\[{\dot{m}}_{\text{ARS}}ex_{9} = {\dot{m}}_{\text{ARS}}ex_{10} + {\dot{\text{Ex}}}_{D,ARS}\]

(32)

Organic Rankine cycle heat exchanger:

\[{\dot{m}}_{\text{gas}}ex_{7} + {\dot{m}}_{\text{ARS}}ex_{11} = {\dot{m}}_{\text{gas}}ex_{8} + {\dot{m}}_{\text{ARS}}ex_{12} + {\dot{\text{Ex}}}_{D,ORC}\]

(33)

Organic Rankine cycle turbine:

\[{\dot{m}}_{\text{ORC}}ex_{12} = {\dot{m}}_{\text{ORC}}ex_{13} + {\dot{W}}_{ORC,TURB} + {\dot{\text{Ex}}}_{D,ORC,TURB}\]

(34)

Organic Rankine cycle condenser:

\[{\dot{m}}_{\text{ORC}}ex_{13} = {\dot{m}}_{\text{ORC}}ex_{14} + {\dot{Q}}_{ORC,COND}\left( 1 - \frac{T_{0}}{T_{b}} \right) + {\dot{\text{Ex}}}_{D,ORC,COND}\]

(35)

Organic Rankine cycle pump:

\[{\dot{m}}_{\text{ORC}}ex_{14} + {\dot{W}}_{ORC,PUMP} = {\dot{m}}_{\text{ORC}}ex_{11} + {\dot{\text{Ex}}}_{D,ORC,PUMP}\]

(36)

The total exergy input to the bottoming cycle in for both models is calculated as:

\[{\dot{\text{Ex}}}_{\text{BC}} = \ {\dot{m}}_{\text{gas}}ex_{6} - {\dot{m}}_{\text{gas}}ex_{8}\]

(37)

where \(ex_{6}\) is the exergy content of the exhaust gas exiting the MGT, and \(ex_{8}\) is the exergy content of the exhaust gas upon its release to the atmosphere.

Similarly, the exergy input required for \(n_{\text{ARS}}\) number of ARS units is calculated as:

\[{\dot{\text{Ex}}}_{\text{ARS}} = \ {\dot{m}}_{\text{gas}}ex_{6} - {\dot{m}}_{\text{gas}}ex_{7}\]

(38)

where \(ex_{7}\) is the exergy content of the exhaust gas leaving \(n_{\text{ARS}}\) number of ARS units, and is fixed by the energy balance equation for the HX_ORC.

These exergy inputs are calcualted with both fluid models and shown in Figure 5. In Figure 5 little difference is observed in the overall exergy input to the bottoming cycle when modelling the exhaust gas as combustion products or as air. Thus, the exergy analysis is carried out with exhaust fluid modelled as air.

 

Figure 5. Exergy inputs for various ARS units. The far right column shows the total exergy input to the bottoming cycle for exhaust gases with inlet and outlet temperatures of 280°C and 150°C respectively

 

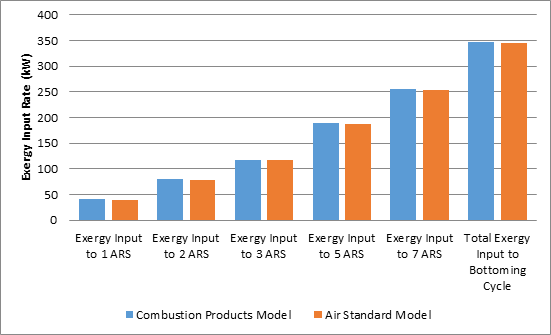
Exergy destruction in each bottoming cycle component is calculated for the 1000 kW unit and is displayed in Figure 6 for each number of ARS units considered. As more ARS units are used, the exergy destruction is seen to increase in the ARS units and ARS heat exchanger, and more exergy from the exhaust stream is used for refrigeration, leaving little for the ORC. Consequently, the exergy destruction in the ORC components decreases as more ARS units are used, leaving less exergy available for utilization in the ORC for electricity generation.

 

Figure 6. Exergy destruction in bottoming cycle components for C1000 turbine configurations

 

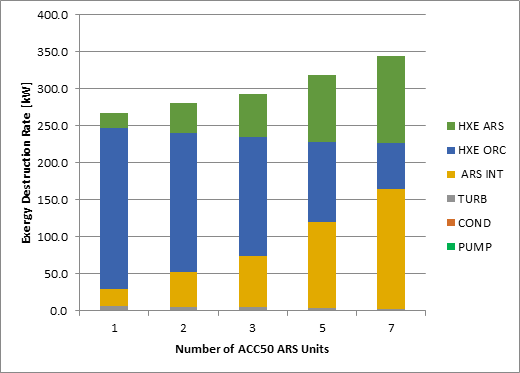
Most of the exergy destruction occurs in the heat exchangers and the ARS units. As little exergy is available to the ORC, the exergy destruction in the ORC turbine, condenser and pump are very small compared to the heat exchangers and ARS units.

Efficiencies of the standalone ARS unit are determined. The energy efficiency can be defined as:

\[\eta_{\text{ARS}} = \frac{\text{Cooling capacity}}{\text{Electrical input + Heat input}}\]

(39)

Using manufacturer technical specifications (SolarNext, 2008), this becomes

\[\eta_{\text{ARS}} = \frac{50}{3\ + 87.96\ } = 55.0\%\]

(40)

The exergy efficiency of the ARS subsystem can be calculated internally as:

\[\psi_{ARS,int} = \frac{Cooling\ capacity \times \left( 1 - \frac{T_{0}}{T_{\text{BC}}} \right)}{Electrical\ input + {\dot{m}}_{\text{ARS}}\left( {\dot{\text{ex}}}_{10} - {\dot{\text{ex}}}_{9} \right)} = 17.0\%\]

(41)

and flow rate of water required to drive the absorption process (SolarNext, 2008). The change in exergy of the stream through the ARS unit is considered to be the exergy input in calculating the internal efficiency.

The change in exergy of the exhaust gas stream across the heat exchanger HX_ARS is considered to be exergy input in calculating the external exergy efficiency of the ARS sub-system as per equation 42. The external efficiency is of particular interest as it can be used to evaluate how well the waste heat stream is being converted into useful work rather than the internal efficiency which is irrespective of the driving heat source.

The external exergy efficiency of the ARS subsystem can be calculated as:

\[\psi_{ARS,ext} = \frac{Cooling\ capacity\ \times (1 - \frac{T_{0}}{T_{C}})}{Electrical\ input\ + {{\dot{m}}_{\text{gas}}\ \dot{(ex}}_{6} - {\dot{\text{ex}}}_{7})}\]

(42)

where T_C and T_H are the boundary temperatures for heat transfer of the hot and cold streams of the unit. Also, T­­_H is taken as the average temperature of the hot water stream the ARS requires, while T_C is taken to be the nominal cold temperature to which the milk is cooled (4°C).

 

Figure 7. Boundaries for exergy efficiency of ARS subsystem. Dotted line denotes boundary for ψ_ARS,ext and dashed line denotes boundary for ψ_ARS,int

 

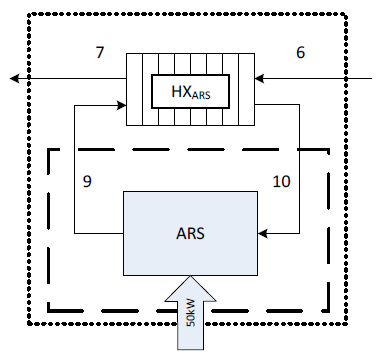
Two definitions of the exergy efficiency, for which the boundaries are illustrated in Figure 7, are considered:

1. Internal exergy efficiency of ARS unit \(\psi_{ARS,int}\). The exergy of the hot stream of water required to run the unit is the input and the exergy of the 50 kW cooling capacity is the output. This exergy efficiency is a constant 17.0%, as it does not consider the exergy of the source providing the heat.

2. External exergy efficiency of ARS unit \(\psi_{ARS,ext}\). The input here is the exergy decrease in the exhaust gas stream across the ARS heat exchanger. This definition highlights how efficiently, from an exergy point of view, the ARS subsystem is integrated into the overall system. This definition is dependent on the number of ARS units, and the exhaust flow conditions of the turbine. indicates the \(\psi_{ARS,ext}\)for each flow condition.

Similarly, energy and exergy efficiencies of the ORC subsystem are developed:

\[\eta_{\text{ORC}} = \frac{{\dot{W}}_{ORC,NET}}{{\dot{m}}_{\text{ORC}}\left( h_{12} - \text{ex}_{11} \right)}\]	(43)
\[\psi_{ORC,int} = \frac{{\dot{W}}_{ORC,NET}}{{\dot{m}}_{\text{ORC}}\left( \text{ex}_{12} - \text{ex}_{11} \right)}\]	(44)
\[\psi_{ORC,ext} = \frac{{\dot{W}}_{ORC,NET}}{{\dot{m}}_{\text{ORC}}\left( \text{ex}_{7} - \text{ex}_{8} \right)}\]	(45)

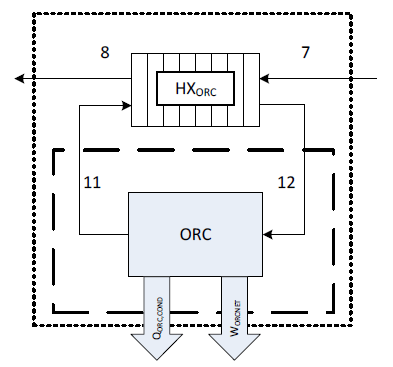
The boundaries for the two ORC exergy efficiency definitions are shown in Figure 8.

 

Figure 8. Boundaries for exergy efficiency of ORC subsystem. Dotted line denotes boundary for ψ_ORC,ext and dashed line denotes boundary for ψ_ORC,int

 

The C1000 turbine configuration efficiencies for the bottoming cycle, the subsystems, and the overall system are listed in Table 7. The energy and exergy efficiencies for variable number of ARS units are also found in Table 7.

 

Table 7. C1000 turbine configuration efficiencies (in percent) Number of ARS units nARS Energy and exergy efficiencies of C1000 with variable ARS units ηORC ψORC,int ψORC,ext ηARS ψARS,int ψARS,ext ηBC ψBC ηSYS ψSYS 1 4.10 37.82 15.74 54.97 16.96 8.88 9.25 10.59 32.41 29.86 2 4.10 37.82 16.05 54.97 16.96 9.00 14.37 10.65 33.71 29.78 3 4.10 37.82 16.38 54.97 16.96 9.12 19.45 10.70 35.01 29.69 5 4.10 37.82 17.14 54.97 16.96 9.40 29.51 10.80 37.61 29.53 7 4.10 37.82 18.03 54.97 16.96 9.72 39.43 10.91 40.22 29.37

 

Figure 9 shows that increasing the number of ARS units leads to higher energy efficiencies in the bottoming cycle and overall system. This is expected, as the internal energy efficiency of the ARS units is higher than that of the ORC, more energy output is produced using the exhaust gases to run the ARS units rather than operating a higher flow rate in the ORC unit, which is only 4.1% energy efficient.

 

Figure 9. Efficiencies for C1000 turbine configurations

 

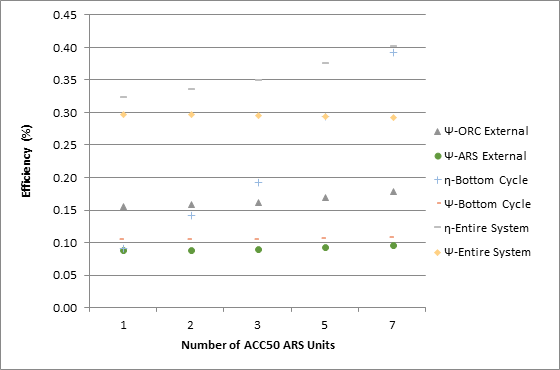
For the same change, the exergy efficiency of the bottoming cycle increases only marginally, since the exergy content of the cooling effect of 50 kW per ARS unit is only slightly higher than the additional 3 kW of electricity required to operate the ARS units. This is illustrated by the lower 16.2% internal exergy efficiency of the ARS units vs. their 55.0% energy efficiency. Adding more ARS units increases the system energy efficiency much more than its exergy efficiency.

The difference in internal and external exergy efficiencies of the ARS and ORC subsystems suggests that the configuration of the systems can be changed to better use the energy available in the exhaust stream to produce work output. For instance, using an ARS system that has a higher temperature input requirement but a higher internal exergy efficiency would make better use of the higher exhaust temperatures available in the ARS heat exchanger.

VALIDATION OF RESULTS AND COMPARISON

An exergy analysis for a gas turbine plant is reported (Ebadi and Gorji-Bandpy, 2005). In that study, second law analysis is used to identify the major contributors of exergy destruction within a gas turbine power cycle. Another study, (Khaliq et al., 2010), demonstrates that 65% of the total exergy destruction of the gas turbine power cycle occurs during combustion. The results from (Ebadi and Gorji-Bandpy, 2005) and (Khaliq et al., 2010) are consistent with and similar to those of the present study, which identifies the primary source of exergy destruction as the combustion chamber, and the other components within the gas turbine module contribute significantly less. An exergy analysis of a trigeneration system is performed (Ahmadi et al., 2012) and identified the heat exchanger driving an organic Rankine cycle and producing hot water was the second largest contributor of exergy destruction, with the combustion chamber being largest. These finding are consistent with the present study, which found that the cumulative exergy destruction of the heat exchangers are the second largest contributor of exergy destruction within the system. The application of exergy analysis to the dairy industry is reported (Soufiyan and Aghbashlo, 2017). The investigations clearly demonstrated the effectiveness of exergy analysis in determining irreversibilities and losses occurring in dairy processing plants in order to improve their performance. The exergy analysis results and exergy destruction trends observed in the present work are along the lines as observed for a dairy plant case, and agree (Soufiyan and Aghbashlo, 2017). The current work contributes to understanding the influence of exergy efficiencies in gas turbine power cycles with heat recovery options. This increased understanding identifies areas where modifications to the system would lead to increased exergy efficiency.

CONCLUSIONS

An exergy analysis is carried out of a grid-independent environmentally benign dairy farm in Ontario, Canada. It is found that farm sizes between 250 and 6000 cows can have cooling and electricity needs met with a micro gas turbine ranging in capacity from 100 to 1000 kW output while maintaining similar exergy efficiencies. For each component and system configuration, sources of exergy destruction within the system are identified, as is the exergy efficiency of the system configuration. Small farm sizes with one ARS unit are found to be more exergy efficient compared to large farm sizes with more than one ARS unit by a difference of less than 0.5%. The primary source of exergy destruction within the micro gas turbine module is the MGT combustion chamber, which contributes 79% of the exergy destruction of the subsystem. Economic and environmental analyses appear to be merited to investigate the financial feasibility as well as the environmental impact of this type of multi-generation energy system.

Nomenclature

\(\text{AF}\) air to fuel ratio

\(e^{\text{ch}}\) specific chemical exergy (mass based)

\(\text{ex}\) specific exergy (mass based)

\(\dot{\text{Ex}}\) rate of exergy

\(\dot{E}x_{d}\) exergy destruction rate

\(h\) specific enthalpy (mass based)

\(\overline{h}\) specific enthalpy (molar based)

\(\dot{m}\) mass flow rate

\(M\) molar mass

\(\text{mf}\) mass fraction

\(n\) number of moles

\(\dot{Q}\) rate of heat transfer

\(\overline{s}\) specific entropy (molar based)

\(T\) temperature

\(\dot{W}\) rate of work output

Greek letters

\(\eta\) energy efficiency

\(\psi\) exergy efficiency

Subscripts

\(0\) ambient conditions

\(A\) air

\(\text{ARS}\) absorption refrigeration system

\(b\) boundary

\(C\) cold boundary condition

\(\text{CC}\) combustion chamber

\(\text{COMP}\) compressor

\(\text{COND}\) condenser

\(\text{cool}\) cooling effect

\(\text{ext}\) external boundary

\(f\) fuel

\(\text{gas}\) exhaust gases

\(H\) hot boundary condition

\(\text{HX}\) heat exchanger

\(\text{int}\) internal boundary

\(\text{LHV}\) lower heating value

\(\text{MGT}\) micro gas turbine

\(\text{NET}\) net work output

\(\text{ORC}\) organic Rankine cycle

\(P\) product gases

\(\text{PUMP}\) pump

\(\text{REGEN}\) regenerator

\(\text{SYS}\) overall system

\(T\) turbine

\(\text{TC}\) topping cycle

\(\text{TURB}\) turbine

ACKNOWLEDGEMENTS

The authors gratefully acknowledge the support provided by the Natural Sciences and Engineering Research Council of Canada.