INTRODUCTION

Throughout the past 50 years, cooling and thermal management have played a key role in accommodating the increase in power while maintaining component temperatures at satisfactory levels to satisfy performance and reliability of objectives. Thermal management will play a vital role in the coming decade for all types of electronics products. It has been found that for every 2 ºC temperature rise, the reliability of a silicon chip will be decreased by about 10% (Yazawa and Shakouri, 2011). The major cause of an electronic chip failure is due to temperature rise 55% as against other factors which accounts 20% vibration, 19% humidity and 6% dust. So it is a great challenge for the packaging engineers to remove the heat from the electronics chips very effectively. A heat sink is an object that transfers thermal energy from a higher temperature to a lower temperature fluid medium. The fluid medium is frequently air, but can also be water or in the case of heat exchangers, refrigerants and oil. If the fluid medium is water, the ‘heat sink’ is frequently called a cold plate. In thermodynamics a heat sink is a heat reservoir that can absorb an arbitrary amount of heat without significantly changing temperature. Practical heat sinks for electronic devices must have a temperature higher than the surroundings to transfer heat by convection, radiation, and conduction. In electronic systems, a heat sink is a passive component that cools a device by dissipating heat into the surrounding air. Heat sinks are used to cool electronic components such as high-power semiconductor devices, and optoelectronic devices such as higher-power lasers and light emitting diodes (LEDs). Heat sinks are heat exchangers such as those used in refrigeration and air conditioning systems, or the radiator in an automobile.

 

Nomenclature 𝜌-density 𝜇- dynamic viscosity 𝜆-mean free path u, v, w, velocity components, x, y, z Cartesian coordinates V-velocity vector, p-pressure, q-heat flux T-temperature S-source terms 𝜏-viscous stress components \(\forall_{d}\)- Mass flow rates Θ- Temperature difference Rth- thermal resistance σ- Free flow area \(Ps\)-dimensionless spreading resistance \(V_{\text{ch}}\)-heat sink channel velocity \(P_{e}\)- Expansion pressure drop \(P_{f}\)- Frictional pressure drop \(P_{c}\)- Contraction pressure drop \(\mathrm{\Delta}P_{\text{hs}}\)-heat sink pressure drops EGM-Entropy generation minimization 𝜱-viscous dissipation avg-averaged value b-bottom thickness of heat sink f-fluid h-hydraulic in-at inlet of channel out-at outlet of channel s-solid t- top thickness of heat sink opt-optimal Re-Reynolds number

 

The method of entropy generation minimization, introduced by A. Bejan (1996), can be used to design an optimized heat sink by simultaneously assessing the parametric relevance of system parameters as they relate to not only the thermal performance but also viscous effects. The entropy generation associated with heat transfer and frictional effects serves as a direct measure of lost potential for work, or in the case of a heat sink, the ability to transfer heat to the surrounding cooling medium.The thermal performance of heat sink is governed by heat transfer physics. Understanding the temperature distribution across the heat sink with entropy generation minimization is principle focus on the present work.

Mjallal et al. (2018) described Cooling Performance of Heat Sinks Used in Electronic Devices. This paper aims to simulate the heat distribution over a heat sink using Ansys fluent simulation tool to serve the goal of investigating and studying on the heat sink in order to improve the cooling performance. Zhou et al. (2009) presented Minimizing the entropy generation rate of the plate-finned heat sinks using computational fluid dynamics and combined optimization the procedure is employed to a heat sink optimization design problem. The entropy generation rate, as a general criterion for designing a heat sink, is introduced into this paper. EGM based on the Thermodynamics Second Law is able to investigate more characteristics about the heat transfer because it combines at the most fundamental level, the basic principles of thermodynamics, heat and mass transfer, and fluid mechanics. The entropy generation from the heat transfer and frictional effects serve as a direct measure of the potential loss of the work or the ability to transfer heat to the surrounding cooling medium for a heat sink. EGM can simultaneously assess the parametric relevance of system parameters including geometric parameters, material properties and flow conditions as they relate to not only the thermal performance but the viscous effects. The enhancement in thermal performance causes a rise in pressure drop, which increases the load of pumping power. Gharbi et al. (2018) present parametric study on thermal performance of heat sink used for electronic cooling. Introducing copper fins inside a heat sink was examined. A parametric study was performed to maximize the critical time elapsed before reaching the allowable temperature limit for different fin lengths, numbers, and thicknesses for the same copper amount. Zing et al. (2019) presented Analysis of porous filled heat exchangers for electronic cooling. An innovative porous filled heat exchanger is modeled to investigate the cooling effectiveness and temperature distribution at its base subject to a high heat flux. Culham and Muzychka (2001) presented optimization of Plate Fin Heat Sinks Using Entropy Generation Minimization. The procedure is based on the minimization of entropy generation resulting from viscous fluid effects and heat transfer, both in the cooling medium and within the internal conductive path of the heat sink. The model clearly demonstrates a rapid, stable procedure for obtaining optimum design conditions without resorting to parametric analysis using repeated iterations with a thermal analysis tool. The results for the six cases presented in the course of demonstrating the feasibility of the model are summarized. Chen et al. (2012) conducted investigation of heat transfer characteristics in plate-fin heat sink. The present study proposes the inverse method and the commercial software of FLUENT in conjunction with the experimental temperature data to determine the average heat transfer coefficient h, heat transfer coefficient based on the fin base temperature and fin efficiency for various fin spacing. An interesting finding is that the calculated fin temperatures obtained from the commercial software are in good agreement with the experimental temperature data at various measurement locations. Su et al. (2016) presented Performance evaluation and optimum design of a new-type electronic cooling device. The optimal operating regions of the device are determined. Compared with the traditional electronic cooling device with a single energy filter between the cold and hot reservoirs. Ndao et al. (2009) conducted Multi-objective thermal design optimization and comparative analysis of electronics cooling technologies. Single objective optimization of either the thermal resistance or pumping power may not necessarily yield optimum performance. The multiple-objective optimization approach is preferable as it provides a solution with different trade-offs among which designers can choose from to meet their cooling needs. The choice of a coolant has a significant effect on the selection of a cooling technology for a particular cooling application and should, therefore, be taken into consideration along with other design factors, such as geometric configuration, system mass, volume, cost, manufacturability, and environmental benevolence. The offset strip fin heat sink outperformed the other cooling technologies. Next to the offset strip fin heat sink in performance are the staggered and in-line circular pin-fin heat sinks, with the staggered arrangement displaying slightly better performance than the in-line arrangement. For relatively very low pumping powers, the micro-channel heat sinks offer lowest thermal resistances. Ismail et al. (2008) conducted A CFD-based experimental analysis on the effect of free stream cooling on the performance of microprocessor heat sinks. The experimental and simulation studies have been made for the Pentium III and IV, AMD Athlon and AMD Duron heat sinks. The total surface area and fin spacing significantly affects the heat sink performance. The higher surface area and suitable fin density will provide better heat sink performance. The higher Reynolds numbers provide higher Nusselt number and lower thermal impedance. The simulation results obtained show close agreement with the experimental result and the Pentium IV heat sink has shown highest performance in removing heat compared to other heat sinks. Huang et al. (2011) conducted A three-dimensional heat sink module design problem with experimental verification. Three types of heat sinks were considered in the optimal design process and the objective of minimizing the maximum temperature in the fin array can always be achieved. Results based on the numerical experiments show that the optimum fin height H and fin thickness W tend to become higher thinner than the original fin array, respectively, as a result both the fin pitch D and heat sink base thickness U are both increased. The temperature distributions for optimum heat sink modules are measured using thermal camera and compared with the numerical solutions. Results show that the measured temperatures match quite well with the calculated temperatures and this is a good reference to justify the validity of the present design algorithm. Koyuncuoglu et al. (2012) conducted heat transfer and pressure drop experiments on CMOS compatible microchannel heat sinks for monolithic chip cooling applications. A novel microchannel heat sink fabrication technique has been developed for the liquid cooling of integrated circuits. The design allows the monolithic implementation of the heat sink with a CMOS compatible fabrication process requiring no change in the layout of the electronic circuit. The monolithic design minimizes the thermal resistance introduced by the heat sink. The experiments indicated that the fabricated microchannel heat sinks are capable of cooling high heat flux electronic devices such as CPUs. During the tests, heat flux values up to 50 W/cm² were successfully removed from the entire chip surface. A single channel heater, simulating a hot spot on a CPU was operated successfully up to 127 W/cm² heat flux. do Nascimento et al. (2013) conducted an experimental study on flow boiling heat transfer of R134a in a microchannel-based heat sink. Heat fluxes up to 310 kW/m², corresponding to heat transfer coefficients of 36 kW/m² were dissipated. For mass velocities lower than 1000 kg/m²s, a wall superheating excess is necessary for the onset of nucleate boiling. Under this condition, it seems that the wall superheating excess increases with increasing the liquid subcooling. In case of mass velocities higher than 1000 kg/m²s, the wall superheating excess becomes negligible. By increasing the liquid subcooling at the inlet of the microchannels and the mass velocity, the flow boiling curves move to the right hand side. Therefore, for the experimental conditions evaluated in the present study the heat sink performance improves with decreasing mass velocity and the liquid subcooling at the inlet of the microchannels .For a fixed mean vapor quality, the heat-sink averaged heat transfer coefficient increases with increasing mass velocity.

Among the novel methods for thermal management of the high heat fluxes found in microelectronic devices, microchannels are the most effective at heat removal. The possibility of integrating microchannels directly in to the heat generating substrates makes them particularly attractive. The two important objectives in electronics cooling, minimization of the maximum substrate temperature and reduction of substrate temperature gradients can be achieved by the use of microchannels.

Experimental tests are one of the more popular ways to determine the heat sink thermal performance often ignored in the design process or performed too late when design changes are limited and become too costly. CFD can give an insight into flow patterns that are difficult, expensive or impossible to study using experimental methods.

3D CFD ANALYSIS OF HEAT SINK

Computational Fluid Dynamics (CFD) is a computer-based tool for simulating the behaviour of systems involving fluid flow, heat transfer, and other related physical processes. It works by solving the equations of fluid flow over a region of interest, with specified conditions on the boundary of that region. There are a number of different solution methods that are used in CFD codes.

The most common, and the one on which CFX is based, known as the finite volume technique. In this technique, the region of interest is divided into small sub-regions, called control volumes. The equations are discretized and solved iteratively for each control volume. As a result, an approximation of the value of each variable at specific points throughout the domain can be obtained. In this way, one derives a full picture of the behaviour of the flow.

The process of performing a single CFD simulation is split into four components:

1. Creating the Geometry and Mesh

2. Defining the Physics of the Model

3. Solving the CFD Problem

4. Visualizing the Results in the Post-processor

Creating the Geometry and Mesh

This interactive process is the first pre-processing stage. The objective is to produce a mesh for input to the physics pre-processor. Before a mesh can be produced, a closed geometric solid is required. The geometry and mesh can be created in the Meshing application or any of the other geometry/mesh creation tools. The basic steps involve:

1. Defining the geometry of the region of interest

2. Creating regions of fluid flow, solid regions and surface boundary names

3. Setting properties for the mesh

 

Figure 1a. Heat sink 3D CAD model

 

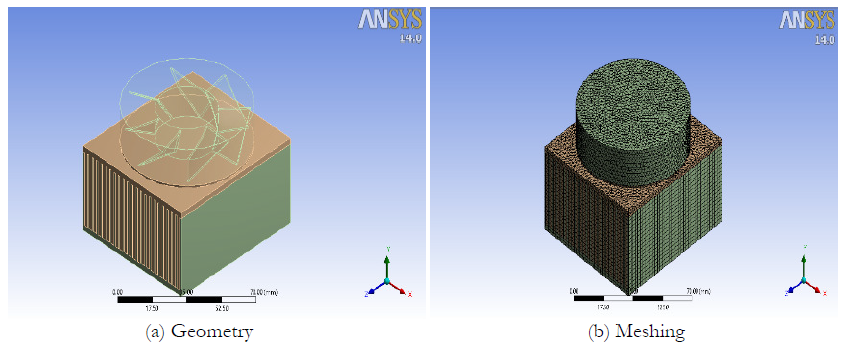
Simulation Parameters used in Solver

1. Inlet boundary condition: mass flow rate in kg/s

2. Outlet boundary condition: static pressure in Pa

3. Heat sink base temperature in °C

4. Surface roughness 10µm

5. Initialization Cartesian velocity (u, v, w) 2m/s

6. Interface of domain

• Inlet heat sink and fan outlet interface

• heat sink fins and fins spacing of air interface

 

Figure 1b. Interface of domain

 

7. Numbers of mesh elements = 336227

8. Turbulence Model: k- ɛ

Solving the CFD Problem

The component that solves the CFD problem is called the Solver. It produces the required results in a non-interactive/batch process. A CFD problem is solved as follows: The partial differential equations are integrated over all the control volumes in the region of interest. This is equivalent to applying a basic conservation law to each control volume.

1. These integral equations are converted to a system of algebraic equations by generating a set of approximations for the terms in the integral equations.

2. The algebraic equations are solved iteratively.

An iterative approach is required because of the non-linear nature of the equations, and as the solution approaches the exact solution, it is said to converge. For each iteration, an error, or residual, is reported as a measure of the overall conservation of the flow properties.

Visualizing the Results in the Post-Processor

The post-processor is the component used to analyse, visualize and present the results interactively. Post-processing includes anything from obtaining point values to complex animated sequences.

Examples of some important features of post-processors are:

1. Visualization of the geometry and control volumes

2. Vector plots showing the direction and magnitude of the flow

3. Visualization of the variation of scalar variables through the domain

4. Quantitative numerical calculations

5. Animation

6. Charts showing graphical plots of variables

7. Hardcopy and online output

Grid Independency Test

Meshing of all zones was done by unstructured mesh using quad and tri elements. Heat sink region has fine mesh as compared to the fan assembly. To optimize no. of grids and to develop grid independency, first very coarse grids were generated and then successively decreasing the size of mesh elements, obtained results were evaluated. To get better grid independency, chosen parameters are change in temperature across the heat sink. Results obtained of above stated parameters under varied no. of total elements are presented in Table 1. Results of mesh ‘e’ are seems optimized. For other grid ‘c’, ‘d’, ‘f’ and ‘g’ results shown negligible variation as compare to results with mesh ‘e’. Hence mesh ‘e’ is finalized for all further simulations to save time and cost of simulation.

 

Table 1. Grid Independency Test Mesh name No. of mesh nodes Tip temperature of heat sink (K) A 16011 334.6 B 85466 336.2 C 96799 339.2 D 116335 341.6 E 139990 343.2 F 1256476 343.4 G 2797424 343.6

 

Figure 2a and 2b indicate the range for temperature contours for aluminium heat sink for different mass flow rate for different temperature respectively. It can be concluded that increase the mass flow rates of air temperature difference is decrease very well. The Figure dictates that there is a temperature rise from base to the outlet of the tip of fins and in the fins. This rise of temperature can be justified due to the heat sink geometry of the fins and the generation of the thermal resistance by the means of heater. Also, the temperature perturbations are quite high near the tip region. With reference to flow rate, it can also be observed that as the flow rate increases, the temperature difference decreases. Also observed from the Figure 1 that on the wall side there is higher temperature drops and on the middle side lower temperature drops which causes temperature flow parabolic.

 

Figure 2. a.Temperature Contours at 363.15K (mass flow rate 5cfm) b.Temperature Contours at 363.15K (mass flow rate 30cfm)

 

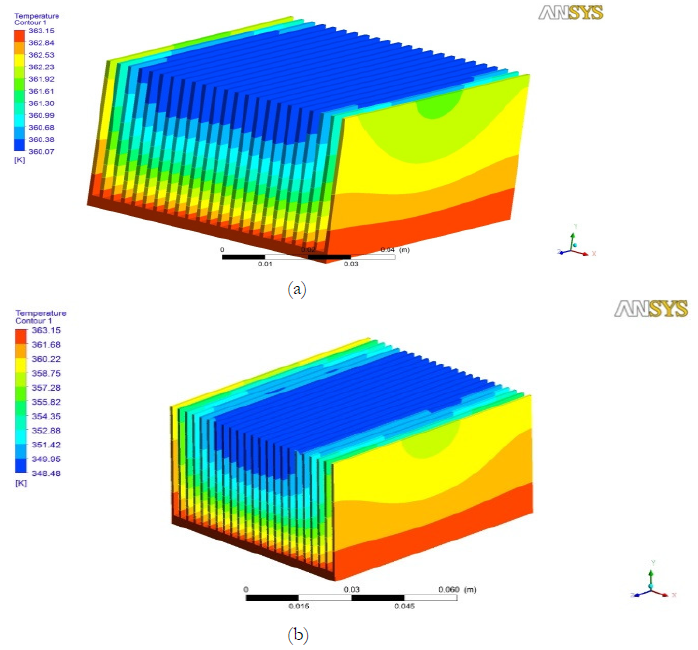
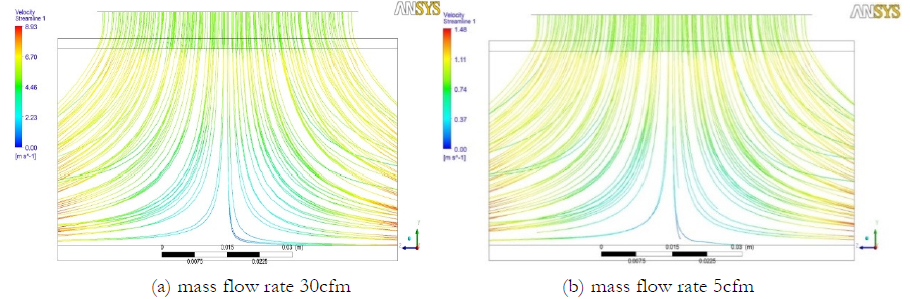
Figure 3 indicate the range for velocity streamlines for different mass flow rates respectively. Range of velocity streamlines is higher 8.93 m/s for the maximum air mass flow rates at 30 cfm. Figure 3 dictate that there is a decrease in velocity in middle portion of the heat sink because of the wall frictional loss. Also indicate that there is rise in velocity at outlet for one particular mass flow rates of air at outlet of fan impeller.

 

Figure 3. a. Temperature Contours at 363.15K (mass flow rate 5cfm) b. Temperature Contours at 363.15K (mass flow rate 30cfm)

 

EXPERIMENTAL SETUP

This chapter contains details of the experimental setup, scheme of instrumentations and experimentation procedures described as under,

1. Description of Experimental Setup

2. Instrumentation scheme

3. Experimental Procedure

Description of Experimental Setup

See Figure 4 and Table 2.

 

Figure 4. (a) Heat sink dimension (b) Aluminum plate fins heat sink (c) Experimental set up

 

Instrumentation Scheme

 

Table 2. Heat sink specification Parameter Dimension Length 78 mm Height 38 mm Width 70 mm Base thickness 3 mm Fin thickness 1 mm Number of fins 23 Fin’s Gaps 2 mm Heatsink material Aluminum

 

In order to estimate the performance of the heatsink suitable instrumentation are employed in the experimental set-up for the estimating various parameters are given as under:

1. Mass flow rate measurement

2. Velocity measurement

3. Temperature measurement

4. Current and voltage measurement

Experimental Procedure

The step-by-step procedure to be adopted for conducting experiments on aluminum plate fins heat sink with fan system is as follows:

• Check all measurement for any errors.

• To set the all the connection and on the main switch.

• Start the fan system running by DC voltage.

• Adjust the air mass flow rates of fan to the desired value with the help of voltage regulator.

• Adjust the heater temperature located heat sink base with variac.

• At the stable condition note down the reading.

• Above experimental procedure can be followed at different sets of mass flow rate of air, for different temperature.

Assumption

The following assumptions are made for the analysis of temperature distribution and heat flow through the fin:

1. Steady state heat conduction.

2. No heat generation within the fin.

3. Uniform heat transfer coefficient over the entire surface of the fin.

4. Homogeneous and isotropic fin material (i.e. thermal conductivity of material constant).

5. Negligible contact thermal resistance.

6. Heat conduction one-dimensional.

7. Negligible radiation.

Experimental results

Figure 5 shows the graph of different mass flow rate of air vs. Tip temperature, Thermal resistance, pressure drops, and velocity respectively. The results suggest that there is with increase in mass flow rate Tip temperature, Thermal resistance, pressure drops are decreases due to heat transfer rates are increases. The above results also suggest that with increase in mass flow rate, there is a rise in velocity.

 

Figure 5. Mass flow rates vs (a) Tip Temperature (b) Thermal resistance (c) Thermal resistance and pressure drops (d) Air velocity

 

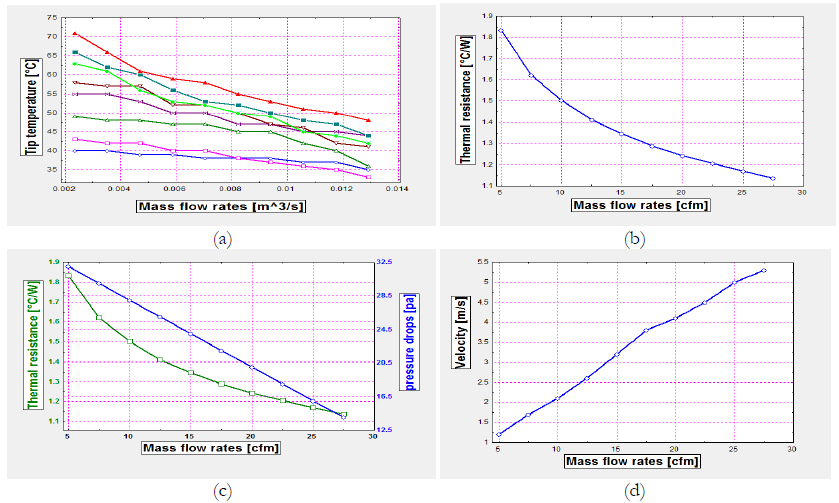
Figure 6(a) shows the graph of base temperature vs. Thermal resistance. The results suggest that increasing the base temperature of heat sink Thermal resistance of heat sink is decreases this is due to Thermal resistance depends on base and tip temperature difference if increasing the base temperature, tip temperature also increase so difference between two temperature is decreasing.

Figure 6(b), (c), (d) shows the graphs of velocity, thermal resistance and Reynolds number. The results suggest that increasing velocity and Reynolds number, Thermal resistance of heat sink decreases this is because of increasing velocity so the rates of heat transfer rates are increasing so difference between base temperature and tip temperature should be decreasing so ultimately the Thermal resistance of heat ink decreasing. The graph between Reynolds numbers vs. velocity. Its shows that increasing velocity, Reynolds number increasing.

 

Figure 6. (a) Thermal resistance with different base temperature (b) Thermal resistance with different air velocity (c) Thermal resistance with different mass flow rates (d) Thermal resistance with different Reynolds number

 

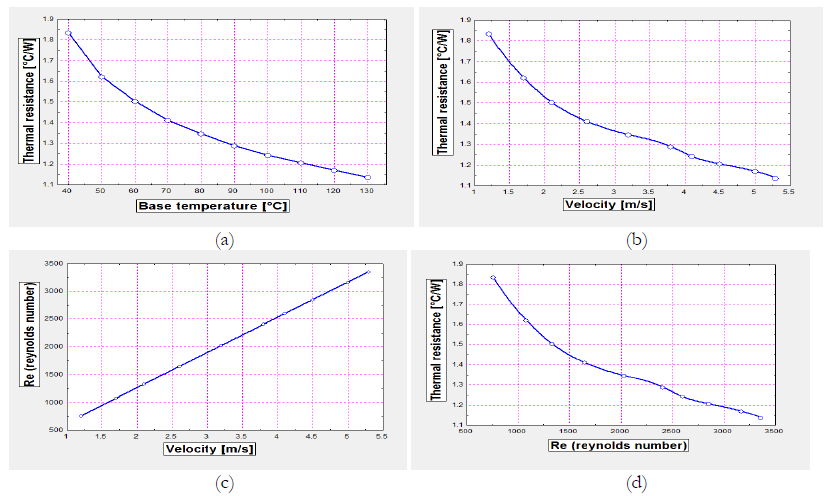
Figure 7 shows the graphs of entropy generation through velocity and base temperature respectively. The results suggest that increasing both velocity and base temperature the entropy generation is also increasing.

 

Figure 7. (a) Entropy generation vs air velocity (b) Entropy generation vs base temperature

 

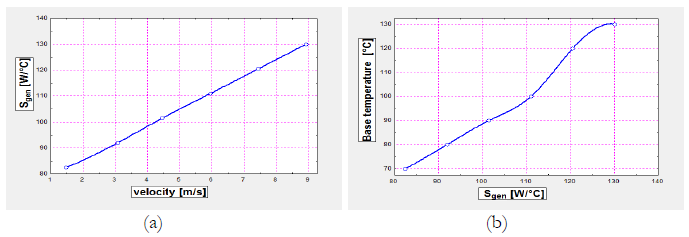
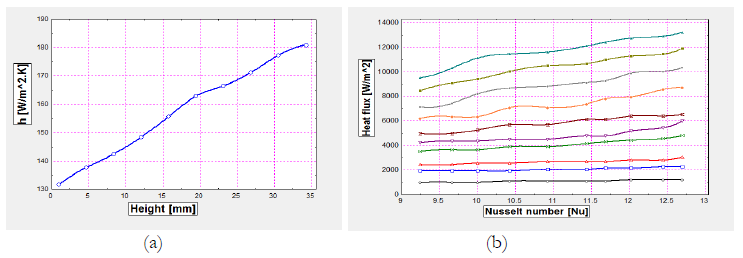
Figure 8 shows the graphs between heat transfer co efficient vs. heat sink height and another graphs shows that Nusselt number vs. heat flux. The results shows that heat transfer co efficient increasing with heat sink height. It does clearly define with difference between base temperature and Tip temperature. Other graph Nusselt number vs. heat flux, the heat flux for all the mass flow rates and temperature it would like to increasing nature.

 

Figure 8. (a) heat transfer coefficient vs heat sink height, (b) heat flux vs Nusselt number

 

MATHEMATICAL MODELLING

The accurate prediction of air flow through a heat sink requires knowledge of the convective heat transfer coefficient for a fin surface using existing forced convection models for a plate fin heat sink assuming developing laminar flow. Laminar flow is a reasonable approximation since the channel hydraulic diameter and flow through the channel are very small, yielding low Reynolds numbers. Using the convection heat transfer coefficient, the total thermal resistance of a heat sink will be modelled using existing models for convection/conduction heat transfer of fins, spreading resistance, thermal joint resistance and conduction resistance for the base plate. The entropy generation is a unique concept that combines both the heat sink resistance and pressure drop. It can be obtained by combining a mass, force, energy, and entropy balance across a heat sink. By minimizing entropy generation with respect to each design variable, the overall thermal performance of a heat sink can be optimized. The present work are divided into the following sections:

• Fluid flow model

• Thermal resistance model

• Entropy generation model

Fluid Flow Model

Pressure Drop Model for a Heat Sink

The pressure drop across a heat sink is expressed as:

\[\mathrm{\Delta}P_{\text{hs}} = P_{c} + P_{f} + P_{e}\]

The contraction pressure drop, Pc can be expressed by the following:

\[P_{c} = K_{c}\left( \frac{1}{2}\rho V_{d}^{2} \right)\]

where the contraction loss coefficient,\(\ K_{c}\) is correlated from the graph of Kays and London (1984) for laminar flow:

\[K_{c} = 1.18 + 0.0015\sigma - 0.395\sigma^{2}\]

The expansion pressure drop \(P_{e}\) can be expressed by the following:

\[\ P_{e} = K_{e}\left( \frac{1}{2}\rho V_{\text{ch}}^{2} \right)\]

where the expansion loss coefficient,\(\ K_{e}\) is correlated from graph of Kays and London (1984) for laminar flow:

\[K_{e} = 1 - 2.76\sigma + \sigma^{2}\]

The frictional pressure drop,\(\ P_{f}\ \)inside the channel is expressed:

\[P_{e} = \frac{{2f}_{\text{app}}\text{Lρ}V_{\text{ch}}^{2}}{D_{h_{\text{ch}}}}\]

The heat sink channel velocity \(V_{\text{ch}}\ \)is expressed by conservation of mass for one channel:

\[V_{\text{ch}} = \frac{V_{d}}{\sigma}\]

where \(s\) is expressed by the following:

\[\sigma = \frac{s}{s + t}\]

Heat Transfer Model

Forced-air cooling through the use of extended surfaces are being used as an attractive technique for cooling microelectronic devices due to its inherent simplicity and cost effectiveness. Designs incorporating such surfaces typically take the form of finned heat sinks. Typically heat sinks are directly mounted on the cases that enclose micro-electronic packages to provide extra surface area for heat transfer from the device to the cooling fluid. The heat dissipated in the package is conducted into the substrate and then transferred by some combination of thermal conduction, convection and radiation to the surrounding through the application of a heat sink.

\[R_{\text{th}} = \frac{T_{b} - T_{a}}{Q}\mathbf{=}\frac{\theta_{b}}{Q}\]

\(R_{\text{th}}\ \)Can be obtained from a resistor network formed between the heat source and the cooling medium.

Figure 9. Thermal circuit of resistor network

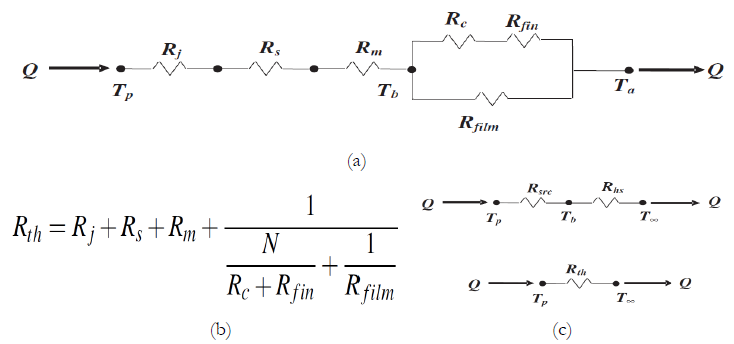
where, N is the number of fins in the heat sink.

Based on the resistor network Figure 9, \(R_{\text{th}}\) can be expressed as:

\[R_{\text{th}} = R_{s} + R_{m} + R_{\text{hs}}\]

• heat sink resistance, \(R_{\text{hs}}\)

\[R_{\text{hs}} = \frac{1}{\frac{N}{R_{\text{fin}}} + \frac{1}{R_{\text{film}}}}\]

• \(R_{s}\) spreading resistance

\[R_{s} = \frac{Ps}{\sqrt{\pi}\text{ka}}\]

• \(R_{m}\) is the conduction resistance encountered by the heat sink base, which depends on the thermal properties of the base material and the geometry of the base. It can be explained by the Fourier law of conduction.

\[R_{m} = \frac{t_{b}}{\text{kA}_{\text{bp}}}\]

Entropy Generation Model

The Entropy Generation Model combines the basic principles of thermodynamics, heat and mass transfer, and fluid mechanics. It is the confluence of thermodynamics, heat transfer, and fluid mechanics because of its interdisciplinary character.

The entropy generation for extended surfaces is defined as the combination of the entropy generated due to fluid effects plus the entropy generated due to thermal effects in the following relationship:

\[S_{\text{gen}} = S_{f} + S_{t}\]

where

\(\ S_{f}\) =Entropy Generation by fan, expressed as:

\[S_{f} = \frac{F_{D}V_{d}}{T_{a}} = \frac{A_{d}{\mathrm{\Delta}P}_{\text{hs}}V_{d}}{T_{a}} = \frac{\forall_{d}{\mathrm{\Delta}P}_{\text{hs}}}{T_{a}}\]

\(S_{t}\)= Thermal Entropy Generation in heat sink, expressed as

\[S_{t} = \frac{Q^{2}R_{\text{th}}}{T_{a}^{2}}\]

Finally entropy generation,

\[S_{\text{gen}} = \frac{\forall_{d}{\mathrm{\Delta}P}_{\text{hs}}}{T_{a}} + \frac{Q^{2}R_{\text{th}}}{T_{a}^{2}}\]

STRUCTURE OF OPTIMIZATION PROBLEMS

Optimization problems require the minimization of a real-valued function \(f(x)\) of an \(N\)-component vector argument \(x = (x_{1},x_{2},\ldots,x_{N})\) whose values are restricted to satisfy a number of real-valued equations

\(h_{k}(x) = 0\), a set of inequalities \(g_{j}(x) \geq 0\), and the variable bounds \(x_{i}^{\left( U \right)} \geq x_{i} \geq x_{i}^{\left( L \right)}\)

The general optimization problem:

Minimize \(f(x)\)

Subject to \(h_{k}\left( x \right) = 0,\ k = 1,2,\ldots,K\)

\(g_{j}\left( x \right) \geq 0,j = 1,2,\ldots,J\)

\(x_{i}^{\left( U \right)} \geq x_{i} \geq x_{i}^{\left( L \right)},i = 1,2,\ldots,N\)

where

\(f(x)\) : Objective Function

\(h_{k}(x) = 0\) : Equality Constraint

\(g_{j}(x) \geq 0\) : Inequality Constraint

\(x_{i}^{\left( U \right)} \geq x_{i} \geq x_{i}^{\left( L \right)}\) : Bounds (Range) for Variables

Strategies for Optimization Program

In order to apply mathematical results and numerical techniques of optimization theory it is necessary to clearly define the performance criteria for which optimized values will be determined, to select the system variables, to define a model that will express the manner in which variables are related and to select the system requirements or constraints for which optimized values will be satisfied.

The strategies for an optimization program can be outlined as:

1. Performance Criterion

2. System Model

3. Selection of Variables and Parameters

4. System Requirement or Constraints

Performance criterion

A performance criterion is needed to judge whether or not a given design is better than another. This criterion is called the objective function. A valid objective function must be influenced by the variables of the design problem. Selection of a proper objective function is an important decision in the design process; it can be minimum cost, maximum profit, minimum weight, minimum energy expenditure, minimum entropy generation associated with the system etc. Based on the analysis of the Entropy Generation (EG) associated with the thermal resistance in a heat sink is considered as the objective function of this optimization program.

System model

Once the performance criterion have been established, the next step is to assemble the model that describes the manner in which the problem variables relate and the way in which the performance criterion is influenced by the variables. A model is the simplified mathematical representation of the system in consideration.

Total entropy generation

\[S_{\text{gen}} = S_{f} + S_{t}\]

where,

\(S_{f}\) =Entropy Generation by fan

\[S_{f} = \frac{F_{D}V_{d}}{T_{a}} = \frac{A_{d}{\mathrm{\Delta}P}_{\text{hs}}V_{d}}{T_{a}} = \frac{\forall_{d}{\mathrm{\Delta}P}_{\text{hs}}}{T_{a}}\]

\(S_{t}\)= Thermal Entropy Generation in heat sink

\[S_{t} = \frac{Q^{2}R_{\text{th}}}{T_{a}^{2}}\]

From Basic Equations for Pressure Drop Model

\(\mathrm{\Delta}P_{\text{hs}}\) Found as:

\[\mathrm{\Delta}P_{\text{hs}} = f(L,H,B,t,s,t_{b,}\rho,\mu,\forall_{d})\]

From Basic Equations for Thermal Resistance Model

\[R_{\text{th}} = f(L,H,B,t,s,t_{b},\rho,\mu,\forall_{d}\mathcal{,l,o,}k,P_{r})\]

Selection of variables and parameters

It is necessary to distinguish between variables whose values influence the operation of the system or affect the design definition, known as decision variables and variables whose values are fixed by external factors, known as parameters.

A heat sink is normally designed based on the system requirement, therefore, heat load (\(Q\)) and source area (\(\mathcal{l \times o}\)) must be fixed prior to designing a heat sink and can be treated as parameters. Selection of the cooling fluid depends on the requirement of application; therefore, properties \((\rho,\mu,C_{p},k_{f})\) of the cooling fluid are fixed for a particular application and can be considered as parameters.

Selection of the heat sink material is normally based on thermal property (\(k\)), cost, weight and machinability, and the material is fixed prior to the design of a heat sink. Therefore, thermal conductivity (\(k\)) is also considered as parameter.

\(T_{a}\) is ambient temperature and assumed as a parameter.

The remaining variables (\(t\), \(s\), \(t_{b}\), \(B\), \(L\), \(H\), \(V_{d}\)) will be treated as decision variables.

Selection of system requirement or constraints

All restrictions placed on a design are collectively called constraints which include limitation on space, performance, geometry, response of the system etc. The constraints are influenced by the decision variables, because only then can they be imposed. If a design satisfies all constraints, then a system can be identified as feasible (workable). Some constraints are quite simple, such as minimum and maximum values of decision variables, while more complex ones may be indirectly influenced by decision variables. Design problems may have equality as well as inequality constrains. A feasible design with respect to an equality constraint, however, must lie on its surface, therefore, the number of equality constraints cannot be more than the decision variables. The feasible region for the inequality constraints is much larger than for the same constraint expressed as equality. It is easier to find feasible designs for a system having only inequality constraints, there is no restriction on number of inequality constraints in optimization model.

The EGM Model has both equality and inequality constraints, which are described below.

Equality constraint

The EGM Model has one equality constraint which is developed from the conservation of energy and must be satisfied during development of an optimum design.

Conservation of energy can be defined as:

\[Q_{\text{in}} = Q_{\text{out}}\]

where \(Q_{\text{in}}\) is the heat input \(Q\) from the package to the heat sink and \(Q_{\text{out}}\) must be equal to \(Q\) in order to ensure conservation of energy.

\(Q_{\text{out}}\) can be obtained by the following relationships:

\[Q_{\text{out}}\ = \ \rho AVC_{p}\left( T_{m} - T_{a} \right) = mC_{p}\left( T_{m} - T_{a} \right)\]

\[T_{m} = \frac{T_{b} + T_{a}}{2}\]

\[T_{m} = R_{\text{th}}Q + T_{a}\]

where \(T_{a}\) is a parameter and \(R_{\text{th}}\) can be obtained from the values of decision variables.

The equality constraint is expressed as:

\[h_{1}\left( Q \right) = Q - Q_{\text{out}} = 0\]

Inequality constraint

The EGM model has many simple inequality constraints that are related with the bound (maximum and minimum values) of the variables and some complex inequality constraints. Complex inequality constraints are described first:

Air flow rate inside the system is restricted by the capacity of the fan because of the nature of the application, and it is expressed as:

\[\forall_{d} \leq \forall_{\text{fan}}\]

The inequality constraint associated with the fan flow rate is expressed as:

\[g_{1}(\forall_{d}) = \forall_{d} - \forall_{\text{fan}} \leq 0\]

The fin efficiency \((\eta_{f})\) is associated with the fin geometry and determines the performance of a fin or a heat sink. The efficiency of a fin is normally expected to be more than 75%. The inequality constraint associated with \(\eta_{f}\) can be expressed as:

\[g_{2}\left( \eta_{f} \right) = 0.75 - \eta_{f} \leq 0\]

Inequality constraint associated with \(N\) can be expressed as:

\[g_{3}\left( N \right) = 2 - N \leq 0\]

Other inequality constraints are simple and associated with the bounds of variables. \(t\), \(s\), \(t_{b}\), \(H\) and \(V_{d}\) must be greater than zero, \(L\) must be greater than or equal to 𝓁 and \(B\) must be greater than or equal to \(w\). \(L\), \(B\), \(H\) and \(t_{b}\) can also be limited to a certain maximum value because of the space and weight restriction associated with the system in consideration. Inequality constraints associated with bounds are given as:

\[g_{4}\left( B \right) = \omega - B \leq 0\]

\[g_{5}\left( B \right) = B - B_{d} \leq 0\]

\[g_{6}\left( L \right)\mathcal{= l -}L \leq 0\]

\[g_{7}\left( L \right) = L - L_{d} \leq 0\]

\[g_{8}\left( H \right) = H - H_{d} \leq 0\]

\[g_{9}\left( t_{b} \right) = t_{b} - t_{\text{bd}} \leq 0\]

where \(L_{d}\), \(B_{d}\), \(H_{d}\) and \(t_{\text{bd}}\) are the upper bound for \(L\), \(B\), \(H\) and \(t_{b}\) because of the space and weight restriction. Table 3 shows the optimization structure of the EGM Model.

Optimization Concept

From Table 3, it is clear that the EGM model deals with a nonlinear objective function with both equality and inequality constraints. The optimization routine will be run in Maple Mathematical Software that uses the Box’s Complex Method nonlinear programming (NLP) procedure based on Kuhn-Tucker’s theory of nonlinear optimization with both equality and inequality constraints.

 

Table 3. Optimization structure of egm Objective function f (Sgen) - non linear Decision variable Heat sink geometry \(t\), \(s\), \(t_{b}\), \(B\), \(L\), \(H\) Fan velocity \[V_{d}\] Parameters Heat input Q Heat sink materials K Cooling fluid properties \(\rho\), \(\mu\), \(C_{p}\), \(k_{f}\) Package geometry \(\mathcal{l}\), \(\omega\) Ambient temperature \[T_{a}\] Equality constraints \[h_{1}\left( Q \right) = Q - Q_{\text{out}} = 0\] Inequality constraints \[g_{1}(\forall_{d}) = \forall_{d} - \forall_{\text{fan}} \leq 0\] \[g_{2}\left( \eta_{f} \right) = 0.75 - \eta_{f} \leq 0\] \[g_{3}\left( N \right) = 2 - N \leq 0\] \[g_{4}\left( B \right) = \omega - B \leq 0\] \[g_{5}\left( B \right) = B - B_{d} \leq 0\] \[g_{6}\left( L \right)\mathcal{= l -}L \leq 0\] \[g_{7}\left( L \right) = L - L_{d} \leq 0\] \[g_{8}\left( H \right) = H - H_{d} \leq 0\] \[g_{9}\left( t_{b} \right) = t_{b} - t_{\text{bd}} \leq 0\]

 

The Kuhn-Tucker theory finds vectors \(x(n \times 1)\), \(u(1 \times J)\), and \(v(1 \times K)\) for the given problem that satisfies the following conditions:

\[\nabla f\left( x \right) - \sum_{j = 1}^{J}{u_{j}\nabla g_{j}\left( x \right) -}\sum_{k = 1}^{K}{v_{k}\nabla h_{k}\left( x \right)} = 0\]

\(h_{k}\left( x \right) = 0\) for \(k = 1,2,\ldots,K\)

\(g_{j}\left( x \right) \geq 0\) for \(j = 1,2,\ldots,J\)

\(u_{j}g_{j}\left( x \right) = 0\) for \(j = 1,2,\ldots,J\)

\(u_{j} \leq 0\) for \(j = 1,2,\ldots,J\)

where \(u_{j}\) and \(v_{k}\) are Kuhn-Tucker multipliers for inequality and equality constraints.

For notational convenience the decision variables of this optimization problem can be redefined as follows in terms of \(x\):

\[x = (x_{1},x_{2},x_{3},x_{4},x_{5},x_{6},x_{7}) = (t,s,t_{b},B,L,H,V_{d})\]

Constraints can be redefined as:

Equality constraint:

\[h_{1}\left( x \right) = Q - Q_{\text{out}} = 0\]

Inequality constraints:

\[g_{1}(x) = \forall_{d} - \forall_{\text{fan}} \leq 0\]

\[g_{2}\left( x \right) = 0.75 - \eta_{f} \leq 0\]

\[g_{3}\left( x \right) = 2 - N \leq 0\]

\[g_{4}\left( x \right) = \omega - x_{4} \leq 0\]

\[g_{5}\left( x \right) = x_{4} - B_{d} \leq 0\]

\[g_{6}\left( x \right)\mathcal{= l -}x_{5} \leq 0\]

\[g_{7}\left( x \right) = x_{5} - L_{d} \leq 0\]

\[g_{8}\left( x \right) = x_{6} - H_{d} \leq 0\]

\[g_{9}\left( x \right) = x_{3} - t_{\text{bd}} \leq 0\]

 

Table 4. Available System Information Item Specifications Heat Source 𝓁=25mm ω=15mm Q=200 W Cooling Fluid – Air \(\rho = 1.2 \frac{\text{kg}}{m^{3}}\) \(\mu = 1.8 \times 10^{-5} \frac{\text{N.s}}{m^{2}}\) \(C_{p} = 1007 \frac{J}{\text{kg.K}}\) \(k_{f} = 25.74 \times 10^{-3} \frac{W}{\text{m.K}}\) \(P_{r} = 0.7\) Heat Sink Material – Al \(k = 250 \frac{W}{\text{m.K}}\) Ambient Temperature \(T_{a}\) = 298 K Fan Capacity 40 CFM Design Constraints \(L_{d}\) = 78 mm \(B_{d}\) = 70 mm \(H_{d}\) = 38 mm \(t_{\text{bd}}\) = 3 mm

 

Optimization Techniques

Optimization can be done using the following two techniques:

1. Parametric Optimization

2. Multi-variable Optimization

Parametric optimization

The rate of entropy generation given in Eq. 6.1 can be used to optimize for any or all variables. The simplest approach is obtained by fixing all variables in the heat sink design but one and then monitoring the change in entropy generation as that particular design variable is freed to float over a typical range. A distinct minimum will be established that represents the magnitude of the free variable that leads to the lowest rate of entropy generation. This technique of optimization is known as parametric optimization.

Parametric optimization needs initial guess of all variables except one to start the parametric optimization for that particular variable. The values of variables are assumed as follows:

\(L\) = 50.0 (mm); \(H\) = 25.0 (mm); \(B\) = 50.0 (mm); \(t\) = 1.0 (mm);

\(s\) = 2.5 (mm); \(N\) = 15; \(t_{b}\) = 5 (mm); \(V_{d}\) = 2 (m/s)

Optimized data after parametric optimization

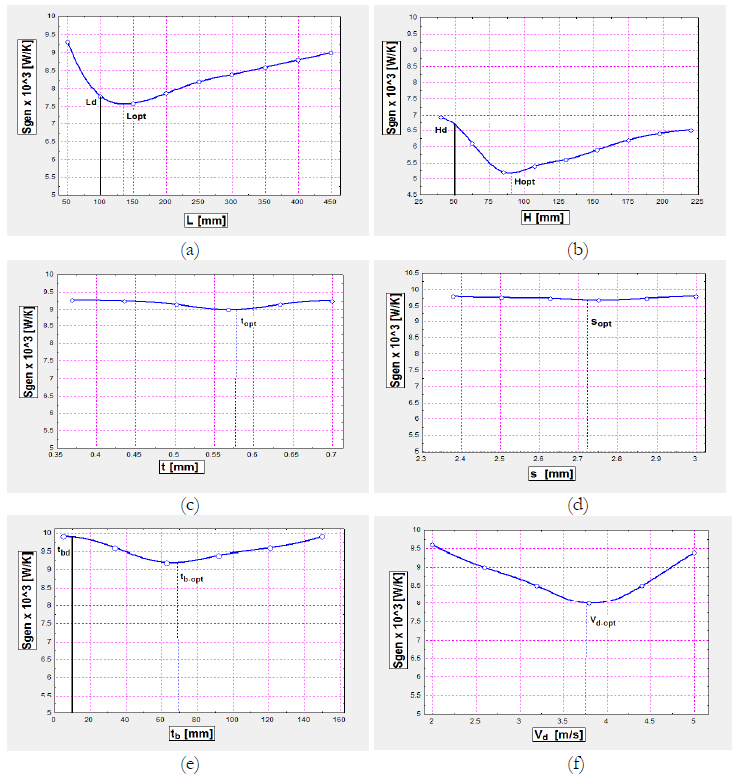
Tables 5 and 6 show the optimized data for minimum entropy generation after parametric optimization. A heat sink designed with all parametric optimized data shows lower entropy generation than the entropy generation associated with each single variable [Table 5 and Figure 10].

 

Table 5. Single Variable Optimized Dimensions of a Heat Sink Geometric Variable Optimized data Dimension Sgen x 103 (W/K) L 100 mm 8.21 H 50 mm 6.17 B 100 mm 5.05 T 0.505 mm 9.16 S 2.64 mm 9.58 N=33 tb 10 mm 9.55 Vd 3.58 m/s 8.1 All Sgen =4.64 x 10-3 W/K

 

Figure 10. Heat sink geometry

 

After Parametric Optimization, the temperature excess (T_base – T_tip) of the optimized heat sink is found to be 8 °C [Table 6].

 

Table 6. Performance of an Optimized Heat Sink Parameter Values Tbase – Ttip 8 oC Rth 0.294 K/W ΔP 9.94 Pa ∀d 156 CFM Power P 0.73 W

 

Figure 11. Influence of individual variable on Sgen

 

Multi variable optimization

While single variable parametric optimization can provide an optimum design condition when all other design variables are predetermined, there is no guarantee that this “Optimized” data will hold when other design variables are unconstrained. Optimization must be achieved based on a simultaneous solution considering all decision variables with equality and inequality constraints. This can be accomplished by incorporating a multi-variable Kuhn-Tucker Method where the minimizing is invoked for each variable, leading to a series of nonlinear equations that must be solved in a simultaneous manner. When the variables are freed to float, some variables such as \(L\), \(B\), \(H\) and \(t_{b}\) show the tendency to become as large as possible to attain higher heat sink performance for minimum entropy generation rate, which is not practical because of the restriction of space (\(L_{d}\), \(B_{d}\), \(H_{d}\)) and cost or weight (\(t_{\text{bd}}\)) of the heat sink. Heat Sink designers should be aware of these restrictions prior to initiating the design process. During the optimization process, optimum values for \(L\), \(B\), \(H\) and \(t_{b}\) are found similar to \(L_{d}\), \(B_{d}\), \(H_{d}\) and \(t_{\text{bd}}\).

Tables 7 and 8 shows the dimensions and performance of a multi-variable optimized heat sink and compare these data with that of a parametric optimized heat sink. Optimized values are different for each case. But there is a trade-off, this higher performance is achieved with the expense of higher fan power. But in the case of entropy generation minimization, which deals with the minimization of both thermal and hydraulic resistance, it is found that optimized heat sinks exhibit a slightly poorer thermal performance but a very good hydraulic performance. It needs very small amount of fan power compared to the heat sinks obtained from parametric optimization. After multi-variable optimization, the temperature excess (T_base-T_tip) of the optimized heat sink is found to be 9.12 °C, which is higher than that of single variable (T_base-T_tip =8 °C) optimized heat sink [Table 8].

 

Table 7. Dimensions of an Optimized Heat Sink Variables Multi variable Single variable Units L 100 100 mm H 50 50 mm B 100 100 mm t 0.95 0.505 mm s 3.05 2.64 mm N 26 33 - tb 10 10 mm Vd 1.77 3.28 m/s

 

Table 8. Performance of an Optimized Heat Sink Parameters Multi variables Single variable Units Sgen 0.0031 0.00464 W/K Tbase-Ttip 9.12 8 °C Rth 0.365 0.294 K/W ΔP 3.57 9.94 Pa ∀d 84 156 CFM Power 0.142 0.73 W

 

CFD AND EXPERIMENTAL RESULTS COMPARISONS OF HEAT SINK

Figure 12 indicate for aluminium heat sink for different Mass Flow rate for different temperature and Thermal resistance respectively. Range of temperature for aluminium heat sink lies between 343.15 K to 332.99 K for different mass flow rates at 70°C temperature, same way for different temperature range 90°C, 110°C, 130°C temperature for aluminium heat sink lies between 403.14 K to 332.99 K respectively. From the range it can be concluded that increase the mass flow rates of air temperature difference is decrease very well. The Figure dictates that there is a temperature rise from base to the outlet of the tip of fins and in the fins. This rise of temperature can be justified due to two main reasons. Due to the heat sink geometry of the fins and second due to the generation of the thermal resistance by the means of heater. Also, the temperature perturbations are quite high near the tip region. With reference to flow rate, it can also be observed that as the flow rate increases, the temperature difference decreases. From Figure 12(a) and Figure 12(b) that on the wall side there is higher temperature drops and on the middle side lower temperature drops which causes temperature flow parabolic.

 

Figure 12. CFD and Experimental Results Comparison for mass flow rates vs. (a) Tip temperature, (b) Theta (θ), (c) Thermal resistance

 

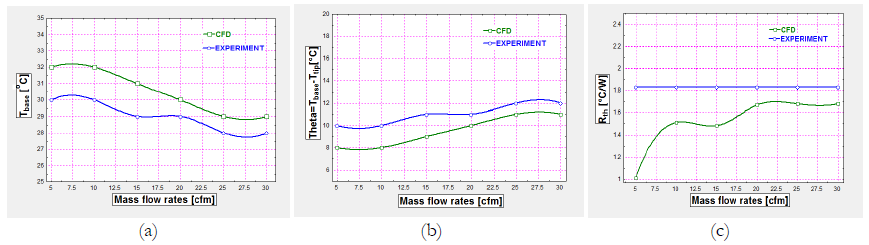
Figure 13 indicate the range for velocity for different mass flow rates and Thermal resistance respectively. Range of velocity streamlines for aluminium heat sink’s fan 0 to 8.93 m/s for different air mass flow rates for all the temperature 70°C, 90°C, 110°C, 130°C. Range of velocity streamlines is higher 8.93m/s for the maximum air mass flow rates at 30 cfm.

 

Figure 13. CFD and Experiment Results Comparison for (a) mass flow rates vs. Velocity (b) velocity vs. thermal resistance (c) mass flow rates vs. Reynolds number

 

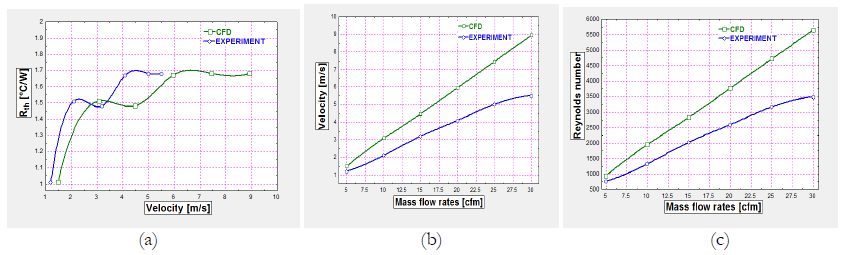
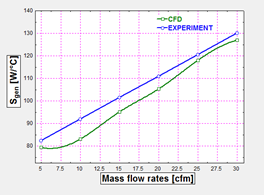
Figure 14 indicates the range for different mass flow rates vs. entropy generation respectively. Range of pressure contour for aluminium heat sink’s fan 5cfm to 30 cfm for different air mass flow rates for all the temperature 70°C, 90°C, 110°C, 130°C. Range of entropy generation is higher 130 W/°C for the maximum air mass flow rates at 30 cfm.

 

Figure 14. Mass flow rates vs. Entropy generation

 

Concluding Remarks

• The numerical results in all cases are observed to be higher of the order of about 2% to 12% as compared to the experimental results in case of majority of the performance parameters of interest. The deviations are minor for mass flow rates and Thermal resistance.

• The major cause for this deviation may be attributed to varying degree of turbulence, flow separation, flow reversal generation, temperature distribution, and velocity stream lines investigated in the present work.

• Further, the observed performance is strongly correlated with flow physics as observed in pressure, velocity streamline and pressure contours obtained through CFD studies.

CONCLUSION

• The maximum temperature is located at heated base surface of heat sink, below the channel outlet. This is due to the low velocity of the fluid flow and resulting high concentration of heat flux.

• The average heat transfer coefficient, average Nusselt number variations decreases along the flow direction due to growing boundary layer thickness and extremely high at the entrance region and the very thin local boundary layer. As the heat flux increase, the average heat transfer coefficient and average Nusselt number also increases for constant pressure drop.

• It should be noted that since the grid size in the flow direction is relatively coarse, the heat transfer is not as accurate as the case for the x and y-direction. However the resolution is sufficient to aid in the design of heat sinks for industrial applications and also to provide information and insight in to the fluid flow characteristics in the flow direction.

• The present analysis and experimental data strongly indicate that the forced convection air cooled heat sink has a superior potential for application in thermal management of the electronic packages. The heat sink is compact and is capable of dissipating a significant thermal load with a relatively small increase in the package temperature.

This study will benefit the design engineers involved in electronic cooling. Using the approach presented in this work, the design engineers can carry out optimization of parametric CAD models,for the selection or design of heat sink for effective thermal management, saving energy and sustainable development in their electronic assemblies.