Abstract
The studied work presents the kinetics of the esterification of Free Fatty Acids (FFA) in jatropha oil with methanol (Alc) using glycerol based solid acid catalyst (SAC) at varying catalyst mass concentrations from 2.5 to 4.0 %, temperature 50-65 °C that is upto refluxing temperature and atmospheric pressure and Alc-FFA mole ratios ranging from 7.2:1 to 28.8:1 with respect to the FFA present in the oil matrix. The optimized esterification parameters were observed as 3.5% mass concentration of glycerol based SAC with 21.6:1, Alc-FFA mole ratio at temperature of 65 °C for a time period of 4 h which provided a conversion of about 97.03%. Based on the experimental results a second order kinetic model is proposed. The temperature influence on the rate of the reaction, Arrhenius constants and activation energies were evaluated. The reaction heat and energy of activation for the reaction were found to be 10.315 kcal/mol and 11.38 kcal/mol respectively.
Keywords
License
This is an open access article distributed under the Creative Commons Attribution License which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Article Type: Research Article
EUR J SUSTAIN DEV RES, Volume 4, Issue 2, 2020, Article No: em0116
https://doi.org/10.29333/ejosdr/7594
Publication date: 25 Jan 2020
Article Views: 3744
Article Downloads: 3809
Open Access HTML Content References How to cite this articleHTML Content
INTRODUCTION
In India, about 70% of the current oil demand for transportation sector has to be imported because India relies heavily on oil imports. Liquid fuels from renewable sources have been projected to be alternate sources of energy for petrol and diesel. To be precise, biodiesel is a promising candidate which has the ability to get going the energy supply with reduced oil imports. Biodiesel also known long-chain fatty acid methyl esters (FAME) is synthesized using renewable raw materials like plant derived oilseeds or fat from animal sources likepalm, canola, soybean etc (Antolin et al., 2002; Al-Widyan & Al-Shyoukh, 2002; Berchmans & Hirata, 2008). However, they being expensive and limited in sources, their application for biodiesel is sparce and hence prompted some researchers to focus on waste cooking, used oils and fats derived animals as feed for biodiesel preparation (Zhang et al., 2003). Tree borne oils like karanja and jatropha oils add value to biodiesel industry by projecting themselves as potential feed sources.
There are several implications of heterogeneous catalysts over homogeneous catalysts like insolubility in the product i.e. simplification of product isolation, catalyst recyclability and process intensification in both modes of operation. Literature cites various SAC for of FFA esterification in oils such as Zn5(OH)8(NO3)2 · 2H2O (Cordeiro et al., 2008), WO3/ZrO2 (Park et al., 2010), new sulfonic acid ion-exchange resins (Russbueldt et al., 2009; Ozbay et al. 2008), Fe2(SO4)3/C (Mengyu et al., 2009).
A pilot-scale fixed bed reactor was used by Lianhua et al. (2010), where acidity was reduced by 90.21%. Pasias et al. (2006) studied FFA esterification in plant based oils at 90-120 °C under pressure. Corro et al. (2010) esterified FFA in crude jatropha oil using SiO2 pretreated with HF as catalyst. Ni and Meunier (2007) used silica-based Nafion resin for the esterification of FFA in a batch and fixed bed-reactor and the results indicated equal conversions in both the cases. In addition, continuous flow reactions were performed by Tesser et al. (2010), Pirola et al. (2014) and Santacesaria et al. (2007).
Marchetti et al. (2007) studied esterification in frying oil using Dowex based basic resins reporting conversion of 80%. Work on tin (II) chloride catalysed FFA esterification in crude jatropha oil was reported by Kusumaningtyasa et al. (2014) at 40-60 °C for 4 hours with Alc to oil ratio of 15:1 to 120:1 and 2.5 to 15% w/w of catalyst wrt to oil. Silica sulfuric acid (SSA) and Taguchi orthogonal array method was used by Shah et al. (2014). There are also some review articles which discussed catalytic esterification and transesterification at length (Jothiramalingam & Wang, 2009; Kombe et al., 2013; Sania et al., 2014).
Recent literature reveals documented reports on the esterification of free fatty acids using solid catalyst (Hood et al., 2018; Michelle et al., 2016; Nuithitikul et al., 2017; Pereira et al., 2018; Veillette et al., 2017; Yunus et al., 2016) such as corn cob (Hussain & Kumar, 2018), tin, gelular exchange resin based catalyst, solid heteropolyacid catalyst (Gaurav et al., 2019), HSO3-functionalized halloysite nanotubes (Silva et al., 2018), acidic metal oxides with supported polyoxometalate catalysts (Avramidou et al., 2017) etc.
A novel SAC was prepared using crude glycerol/glycerol/commercial glycerol and sulphuric acid (Prabhavathi et al., 2009) employing thermal treatment. The catalyst proved to be efficient as the -SO3H groups are successfully attached and possess good thermal stability with more hydrogen moieties which heightened the catalytic activity towards various chemical modifications and its reusability. It may possibly lead to the replacement of traditionally used homogeneous sulfuric acid, thus making the chemical processing industries green and economically more profitable, counteracting the effluent treatment as well. For the first time, kinetic mechanism of glycerol based SAC was performed and reported here for esterification of FFA in jatropha oil by studying the various esterification parameters like reaction time, temperature, catalyst amount and FFA/Alc ratio.
The objective of the present study is to determine the intrinsic kinetic parameters of the system namely solid acid esterification of FFA in jatropha oil with a view to contribute in the design aspects of a reactor system as a prerequisite for biodiesel preparation.
MATERIALS AND METHODS
Jatropha oil was purchased from a near-by rice mill (Telangana). Methanol (99.5%) used in the experiments was of high purity grade and supplied by Sd. Fine chemicals, Mumbai (directly used without any pretreatment). AOCS Method (AOCS, 2003) was used to estimate acidity of the oil (Acid Value (AV)) which varied from 19.4 to 22.2. Conversion of the reaction was determined by estimating the drop in the AV of the starting material and the product by titrimetric analysis. The oil composition was found to be palmitic (16.8%), stearic (6.51%), oleic (37.74%) and linoleic (37.99%) as determined by gas chromatography (Christie, 1972).
Experimental Procedure
The experimental procedure, execution of the experiments and the sampling protocol adopted in this study was similar to our previous work (Rani et al., 2013). For an experimental run, round 250 g of jatropha oil was contacted with 8.75 g SAC and 375 ml Alc at 65 °C at a constant agitation speed of 500 rpm. The experimental matrix comprised the following pattern,
- Different catalyst concentrations, 2.5 to 4%, based on FFA in jatropha oil, Alc-FFA was fixed at 21.6:1, 65 °C.
- Different molar ratios of methanol to FFA, 7.2:1, 14.4:1, 21.6:1 and 28.8:1, at 65 °C and catalyst concentration of 3.5%.
- Different temperatures, 50 to 65 °C, with Alc-FFA mole ratios of 21.6:1 and 3.5% catalyst.
The below eq. was used to calculate FFA conversion
| \[X\left( \% \right) = \left\{ 1 - \left( \frac{A_{\text{final}}\ }{\ A_{\text{initial}}} \right) \right\} \times 100\ \] | (1) |
where A initial is the starting material AV and A final is the AV of the final product.
Statistical Analysis
Statistical significance was measured through regression using ANOVA. The experimental data was shown as the mean ± standard deviation, and was analyzed by a regression using ANOVA to evaluate the level of. A p-value < 0.05 was sufficient enough to determine the significance of results.
Kinetic Model
The intrinsic kinetics of FFA esterification in targeted oil was established based a pseudo-homogeneous model (Rattanaphra et al., 2011). The model was considered to be significant enough to describe the esterification of FFA with Alc in the presence of triacylglycerols using SAC. The reversible reaction of esterification of FFA present in jatropha oil with Alc and SAC is given below:
| \[A + B\ \overset{k_{1}}{\underset{k_{2}}{\Leftrightarrow}}\ C + D\] | (2) |
Rate equation in the rate control step could be depicted as follows
| \[r_{A}\ = \ - \frac{dC_{A}}{\text{dt}} = \ k_{1}\ C_{A}C_{B}\ - \ k_{2}\ C_{C}\ C_{D}\] | (3) |
Where CA : FFA concentration, CB :Alc concentration, CC : FAME concentration, CD : water concentration, k1 & k2 are the kinetic rate constants for the to and fro reactions. Since \(C_{A} = C_{\text{Ao}}(1 - X)\) (X : FFA conversion ,\(C_{\text{Ao}}\) : initial FFA concentration of FFA), \(C_{B} = C_{\text{Ao}}(M - X)\)(\(M\ = \frac{C_{\text{Bo}}}{C_{\text{Ao}}}\):ratio of Alc to FFA initial concentration) and\(C_{C} = C_{D}\ = \ C_{\text{Ao}} - C_{A}\ = \ C_{\text{Bo}} - C_{B}\ = C_{\text{Ao}}X\ \), upon substitution in Eq. [3], we obtain,
| \[\frac{\text{dX}}{\text{dt}} = \ C_{\text{Ao}}^{}\ \lbrack k_{1}\ (1 - X)(M - \ X)\ - \ k_{2}\ X^{2}\rbrack\] | (4) |
At equilibrium, \(\frac{\text{dX}}{\text{dt}}\)= 0
X = XE, , K = Equilibrium constant The above equation becomes,
| \[K = \frac{k_{1}}{k_{2}} = \frac{X_{E}^{2}}{\ (1 - X_{E})(M - \ X_{E})\ }\ \] | (5) | |
|---|---|---|
| \[k_{2} = \ \frac{k_{1}(1 - X_{E})(M\ - X_{E})}{X_{E}^{2}}\ \] | (6) |
Eq. [4] reduces to
| \[k_{2} = \ \frac{k_{1}(1 - X_{E})(M\ - X_{E})}{X_{E}^{2}}\] | (7) |
Integration of Eq. [7] yields,
| \[\text{ln\ }\left( \frac{(2a_{1}X\ - \ M\ - 1\ - \ a_{2})\ ( - \ M\ - 1\ + \ a_{2})}{(2a_{1}X\ - \ M\ - 1\ + \ a_{2})\ ( - \ M\ - 1\ - \ a_{2})} \right) = k_{1}a_{2}C_{\text{Ao}}t\] | (8) |
for
| \[a_{1}\ = \left( 1 - \frac{1}{\ K\ } \right)\] | (9) |
and
| \[a_{2}\ = \left\lbrack \left( M + 1 \right)^{2}\ - \ 4a_{1}M \right\rbrack\ ^{1/2}\] | (10) |
RESULTS AND DISCUSSION
The performance of the SAC for the esterification of FFA in jatropha oil was evaluated and the experimental data obtained was used to optimize the operating parameters like reaction time, temperature, catalyst concentration and methanol-FFA mole ratio.
The influence of agitation speed was examined from 100 to 500 rpm for the esterification of FFA with 21.6:1 Alc-FFA mole ratio, 3.5 % catalyst concentration and 65 °C. The FFA conversion was constant at different speeds of agitation shown in Figure 1, this signifies that the external solid-liquid mass transfer resistance is absent for the swaping of both reactants and products. Therefore, speed of agitation above 500 rpm reflected that effects of external mass transfer contributed negligible impact on the reaction. Henceforth, all the reactions further were performed at 500 rpm.
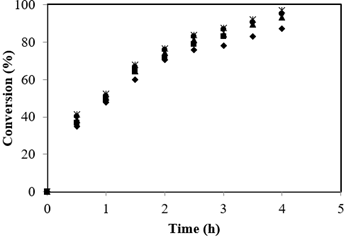
External mass transfer resistance absence was demonstrated by theoretical calculations. Mass transfer coefficients were used to calculate the mass transfer rate was calculated from which in turn were calculated from liquid phase diffusivities. DAB (FFA in methanol) and DBA (methanol in FFA) were calculated using Wilke-Chang equations and found to be 9.806 × 10-6 cm2/s and 4.463 × 10-7 cm2/s respectively. Sherwood number (Yadav et al., 2003) was enumerated to determine the solid liquid mass transfer coefficients kSLA and kSLB values as 1.96 × 10-3 cm/s and 8.92 × 10-4 cm/s. The surface area of the particles per unit liquid volume (ap) was estimated as 8.4 × 10-4 /cm. Conversion profiles were used to calculate initial reaction rate. An observed initial reaction rate was calculated as 9.18 × 10-7 mol/cm3/s. Hence, 1/\(r_{\text{obs}}\) is 1.09 × 106 s/cm3/mol.
The rate of mass transfer/unit volume of the liquid phase (mol/cm3s) at steady state is given by
| \[R_{A} = k_{\text{SLA}}\ a_{p}\lbrack\ \lbrack A_{0}\rbrack - \lbrack A_{s}\rbrack\rbrack\] | (11) |
Which summarizes rate of transfer of A and B from bulk liquid phase to external surface of the catalyst.
| \[R_{A} = k_{\text{SLB}}\ a_{p}\lbrack\ \lbrack B_{0}\rbrack - \lbrack B_{s}\rbrack\rbrack\] | (12) |
and
| \[R_{A}\ = \ r_{\text{obs}}\] | (13) |
The subscripts ‘s’ and ‘o’ indicate the bulk liquid phase concentration and external surface of catalyst concentration.
| \[\frac{1}{r_{\text{obs}}}\ = \ \frac{1}{k_{\text{SLA}}\ a_{p}\lbrack\ \lbrack A_{0}\rbrack\ - \ \lbrack A_{s}\rbrack\rbrack}\ \] | (14) | |
|---|---|---|
| \[\frac{1}{r_{\text{obs}}}\ = \ \frac{1}{k_{\text{SLB}}\ a_{p}\lbrack\ \lbrack B_{0}\rbrack\ - \ \lbrack B_{s}\rbrack\rbrack}\ \] | (15) |
The following inequality is applicable in case of absence of external mass transfer resistance,
| \[\frac{1}{r_{\text{obs}}}\ > > \ \frac{1}{k_{\text{SLA}}\ a_{p}\ \lbrack A_{0}\rbrack}\ \] | (16) | |
|---|---|---|
| \[\frac{1}{r_{\text{obs}}}\ > > \frac{1}{k_{\text{SLB}}\ a_{p}\ \lbrack B_{0}\rbrack\ }\ \] | (17) |
Thus, substituting the values in the above equations, it is observed that
| \[\frac{1}{r_{\text{obs}}}\ > > \ \frac{1}{k_{\text{SLA}}\ a_{p}\ \lbrack A_{0}\rbrack}\ \] | (18) |
i.e. 1.09 × 106 s/ cm3/mol \(\gg\) 24.77
| \[\frac{1}{r_{\text{obs}}}\ > > \frac{1}{k_{\text{SLB}}\ a_{p}\ \lbrack B_{0}\rbrack\ }\ \] | (19) |
i.e. 1.09 × 106 s/ cm3/mol \(\gg\) 1.89
Hence, it can be inferred that there is non-existance of resistance due to the solid liquid external mass transfer for both A and B.
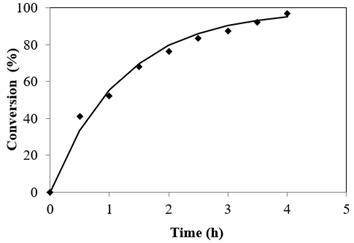
Esterification reaction rate is very much influenced by reaction period. The optimization of the process parameters was performed at catalyst mass concentration of 3.5%, 65 °C, Alc-FFA mole ratio of 21.6:1. Figure 2 depicts that there exista a linear relation between conversion and reaction time. It was found that initially after 30 min of reaction 41.19% conversion was obtained and conversion steered with time and culminated at a maximum value of 97.03% in 4 h. However, no significant increase was recorded in the conversion upon increase in reaction time.
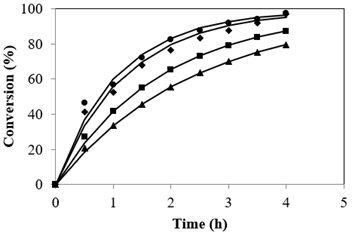
Catalyst loading plays a major role catalytic reactions. The influence of catalyst concentration on the FFA conversion was investigated from 2.5 to 4.0% based on FFA in jatropha oil to determine the optimum SAC load. Results indicated that with increasing catalyst quantity the reaction rate increased. Figure 3 details the profile of conversion with cumulative SAC concentration. The data shows that catalyst concentration of 2.5% gave a conversion of 79.5%, using 3% catalyst, the conversion was found to be 87.3% and increase in catalyst percentage to 3.5% gave 97.03% indicating that conversion, however no prominent change was observed on increasing to 4.0%. The changes in conversions can be explained by the fact that an increase in SAC quantity led to an increase in the number of active sites thereby increasing the conversion, hence the optimal amount of catalyst was found to be 3.5%. Many researchers used varying amounts of different heterogeneous catalysts based on the catalyst active sites. The present study is taken up to establish the concentration of the catalyst required keeping in mind the presence of large amount of triglyceride when compared to the FFA in feed oil.
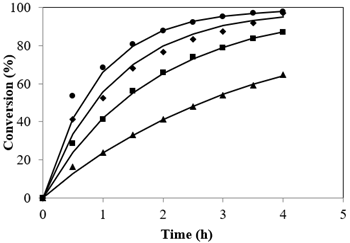
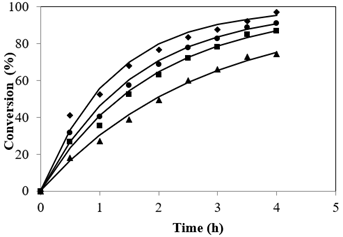
Esterification reactions belong to the equilibrium limited regime. A quick glance at the stoichiometry of esterification reveals equal moles of reactants to yield equal moles of products. The equilibrium shift towards the direction of ester formation is attributed to usage of methanol in excess than is generally used. This leads to the overall increase not only in the rate but also pushes the reaction completion to completion (Tesser et al., 2010). The plot resulted by different Alc-FFA mole ratio on the FFA esterification at SAC concentrations of 3.5% is illustrated in Figure 4 at 65 °C. The influence of Alc to FFA on FFA conversions at various quantities of Alc i.e., from 7.2:1 to 28.8:1 were examined. It was observed that conversion was less for lower ratios of methanol to acid while conversion increased from 64.66% to 98.01% as the mole ratio increased from 7.2:1 to 28.8:1, the highest conversion was 97.03% at 21.6:1 mole ratio and further increase in methanol showed no significant change.
It is a well known fact that FFA esterification is endothermic supporting by the fact that temperature increase has a marked effect on reaction rate. This proportionality is in conformity with the endothermic behavior of esterification since the forward reaction is favored by rise in temperature (Shanmugam et al., 2008). Higher temperatures results in fast reactions, but in case the esterification temperature exceeds Alc boiling point, formation of bubbles occur upon vaporization inhibiting three phase reaction interface. So, the reaction temperature is considered optimum for the esterification of jatropha oil to be around 338.15 K (Liu et al., 2007). Although researchers (Lianhua et al., 2010) have proved that a temperature of 338.15 K is sufficient for complete conversion of FFA. Cordeiro et al. (2008) reported FFA esterification employing layered compound zinc hydroxide nitrate at a temperature of 413.15 K where they claim highest ester yield and Pasias et al. (2006) used a temperature of 90 -120 °C for the FFA esterification.
To determine the effect of temperature on conversion, the reactions were evaluated at temperatures upto refluxing temperatures i.e 50 to 65 °C while maintaining other process variables constant i.e., catalyst mass concentration of 3.5%, methanol/FFA mole ratio of 21.6:1 for 4 h of reaction time. The esterification reactions were carried out upto refluxing temperature and atmospheric pressure, hence further increase in temperature was not possible. The results demonstrated the endothermicity of the reaction. Figure 5 depicts the conversions obtained at studied temperatures and it can be deduced that a rise in temperature to 65 °C from 50 resulted in a steep increase in product formation showing a significant increase in conversion from 74.3% to 97.03%. Maximum conversion rate was achieved at the refluxing temperature of Alc at atmospheric pressure.
Kinetic Interpretation
k1 was calculated from the initial rates method, At zero time, the starting products concentrations, CC and CD, is zero i.e. X =0, hence, Eq. [4] changes to,
| \[\frac{\text{dX}}{\text{dt}}_{t = 0} = k_{1}MC_{\text{Ao}}\] | (20) | |
|---|---|---|
| \[r_{o}\ = \ k_{1}MC_{\text{Ao}}^{}\] | (21) |
The initial rate was calculated for the first 30 min interval and k1 values at different temperatures were calculated from Alc/FFA molar ratios and initial rates using Eq. [20] and the slopes of these plot gives the k1 values. The behaviour of the Alc/FFA molar ratios and initial rates is reflected in Figure 6a. By substituting the k1 values in Eq. [8], k2 was estimated by trial and error such that the slope of the plot of \(\ln\left( \frac{\left( 2a_{1}X - M - 1 - a_{2} \right)\left( - M - 1 + a_{2} \right)}{\left( 2a_{1}X - M - 1 + a_{2} \right)\left( - M - 1 - a_{2} \right)} \right)\) vs \(C_{A0}t\), Eq. [8] converges to the previously guessed value (\(k_{1}a_{2}\)), as shown in Figure 6b at 65 °C, 21.6:1 Alc-FFA mole ratio, 3.5% SAC concentration.
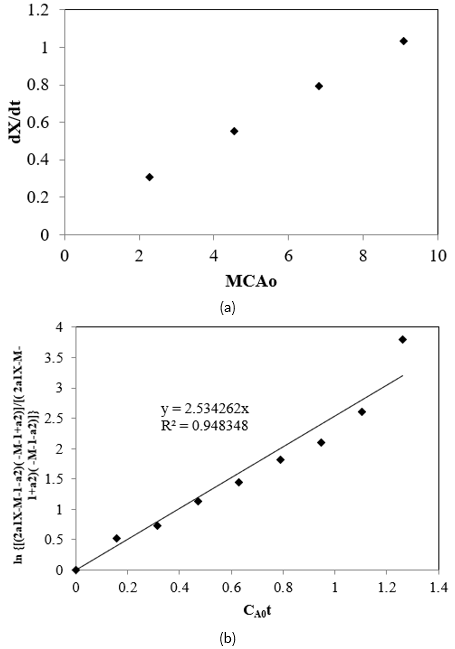
In the similar fashion these kinetic parameters were determined for each experiment (i.e., with varying temperatures and catalyst concentration) by nonlinear regression
. The estimated rate constant and equilibrium constants by nonlinear regression based on experimental data are listed in Table 1. Arrhenius equation was applied to study the temperature effect on the forward reaction rate by fitting k1 and k2 respectively,
|
Table 1. Kinetic rate constants and equilibrium constant for esterification of FFA in jatropha oil using glycerol based solid acid catalyst at different reaction conditions
* at 21.6:1 methanol/FFA mole ratio mole ratio, 65 °C; ** at 21.6:1 methanol/FFA mole ratio mole ratio, 3.5% catalyst concentration |
||||||||||||||||||||||||||||||||||||||||||||||||
| \[k_{1}\ = \ A\text{\ exp\ }\left( \frac{- \Delta E_{}}{\text{RT}} \right)\] | (22) |
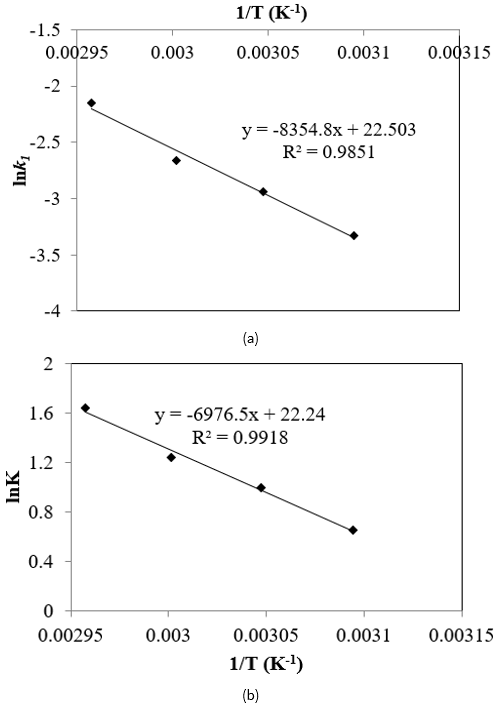
The plot of ln k as a function of the reciprocal temperature as shown in Figure 7a. The frequency factor (A), and the energy of activation (∆E) were obtained as 2.76 x 106 and 11.378 kcal/mol respectively. van’t Hoff equation was applied to study the temperature effect on equilibrium constant, K,
| \[\ln K = \frac{- \Delta H}{\text{RT}} + \text{const}\] | (23) |
The heat of reaction was 10.314 kcal/mol as obtained from Figure 7b which strengthens the endothermicity of the esterification reaction. An activation energy of 10.314 kcal/mol was obtained and is approximately similar to those found by Neji et al. (2011).
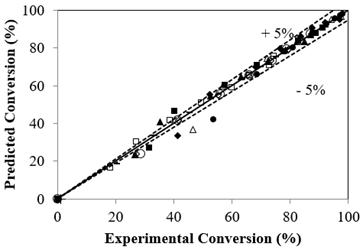
The experimental and calculated conversions from Eq. [8] displayed a ± 5% deviation as shown in Figure 8. Regression analysis by ANOVA shows a p-value of 0.00497 with an R2 value of 0.99 and adopted to be significant enough to profess the satisfactory nature of the reaction system based on the proposed model.
CONCLUSIONS
Experimental results show that FFA in jatropha oil could be effectively reduced to FAME by esterification with methanol, using 3.5% mass concentration of glycerol based solid acid catalyst with methanol/FFA mole ratio of 21.6:1, at 65 °C. A satisfactory relation was achieved between the developed model and experimental data prompting a satisfactory behavior of the developed model in explaining the study undertaken.
ACKNOWLEDGEMENTS
Our sincere thanks to Dr. R.B.N Prasad, Former Head of the Department, Centre for Lipid Research and Technology, CSIR-Indian Institute of Chemical Technology for the execution of this work.
References
- Antolin, G., Tinant, F.V., Briceno, Y., Castano, V., Perez, C., & Ramirez, A.I. (2002). Optimization of biodiesel production by sunflower oil transesterification. Bioresource Technology, 83, 111-114. https://doi.org/10.1016/S0960-8524(01)00200-0
- Al-Widyan, M. I., & Al-Shyoukh, A.O. (2002). Experimental evaluation of the transesterification of waste palm oil into biodiesel. Bioresource Technology, 85, 253-256. https://doi.org/10.1016/S0960-8524(02)00135-9
- AOCS, in: Firestone D. (Eds.). (2003). Official Methods and Recommended Practices of the American Oil Chemists’ Society, 5th Edn., AOCS Press, Champaigne Method Cd 3d-63.
- Avramidou, K. V., Zaccheria, F., Karakoulia, S. A., Triantafyllidis, K. S., & Ravasio, N. (2017). Esterification of free fatty acids using acidic metal oxides and supported polyoxometalate (POM) catalysts. Molecular Catalysis, 439, 60-71. https://doi.org/10.1016/j.mcat.2017.06.009
- Berchmans, H. J., & Hirata, S. (2008). Biodiesel production from crude Jatropha curcas L. seed oil with a high content of free fatty acids. Bioresource Technology, 99, 1716-1721. https://doi.org/10.1016/j.biortech.2007.03.051
- Corro, G., Tellez, N., Ayala, E., & Marinez-Ayala, A. (2010). Two-step biodiesel production from Jatropha curcas crude oil using SiO2·HF solid catalyst for FFA esterification step. Fuel, 89, 2815-2821. https://doi.org/10.1016/j.fuel.2010.04.023
- Cordeiro, C. S., Arizaga, G. G. C., Ramos, L. P., & Wypych, F. (2008). A new zinc hydroxide nitrate heterogeneous catalyst for the esterification of free fatty acids and the transesterification of vegetable oils. Catalysis Communication, 9, 2140-2143. https://doi.org/10.1016/j.catcom.2008.04.015
- Christie, W. W. (1972). The Preparation of the Alkyl Esters from Fatty Acids and Lipids, In: Topics in Lipid Chemistry, Scientific Books Limited, London, 171-198.
- Gaurav, A. Dumas, S., Mai, C. T. Q., & Flora T. T. Ng. (2019). A kinetic model for a single step biodiesel production from a high free fatty acid (FFA) biodiesel feedstock over a solid heteropolyacid catalyst. Green Energy & Environment, 4, 328-341. https://doi.org/10.1016/j.gee.2019.03.004
- Hood, Z. D., Adhikari, S. P., Evans, S. F., Wang, H., Li, Y., Naskar, A. K., Lachgar, M. C. A., & Paranthaman, M. P. (2018). Tire-derived carbon for catalytic preparation of biofuels from feedstocks containing free fatty acids. Carbon Resources Conversion, 1, 165-173. https://doi.org/10.1016/j.crcon.2018.07.007
- Hussain, Z., & Kumar, R. (2018). Esterification of free fatty acids in karanja oil using novel corncob derived solid acid catalyst. Materials Today: Proceedings, 5, 18045-18051. https://doi.org/10.1016/j.matpr.2018.06.138
- Jothiramalingam, R., & Wang, M. K. (2009). Review of recent developments in solid acid, base, and enzyme catalysts (heterogeneous) for biodiesel production via transesterification. Industrial and Engineering Chemistry Research, 48, 6162-6172. https://doi.org/10.1021/ie801872t
- Kombe, G. G., Temu, A. K., Rajabu, H. M., Mrema, G. D., Kansedo, J., & Lee, K. T. (2013). Pre-Treatment of high free fatty acids oils by chemical re-esterification for biodiesel production—a review. Advances in Chemical Engineering and Science, 3, 242-247. https://doi.org/10.4236/aces.2013.34031
- Kusumaningtyasa, R. D., Handayani, P. A., Rochmadia Purwono, S., & Budimana, A. (2014). Tin (II) chloride catalyzed esterification of high ffa jatropha oil: experimental and kinetics study. International Journal of Renewable Energy Development, 3, 75-81. https://doi.org/10.14710/ijred.3.2.75-81
- Lianhua, L., Pengmei, L., Wen, L., Zhongming, W., & Zhenhong, Y. (2010). Esterification of high FFA tung oil with solid acid catalyst in fixed bed reactor. Biomass and This article is not included in your organization's subscription. However, you may be able to access this article under your organization's agreement with ElsevierBioenergy, 34, 496-499. https://doi.org/10.1016/j.biombioe.2009.12.014
- Liu, X., He, H., Wang, Y., & Zhu, S. (2007). Transesterification of soybean oil to biodiesel using SrO as a solid base catalyst. Catalysis Communication, 8, 1107-1111. https://doi.org/10.1016/j.catcom.2006.10.026
- Marchetti, J. M., Miguel, V. U., & Errazu, A. F. (2007). Heterogeneous esterification of oil with high amount of free fatty acids. Fuel, 86, 906-910. https://doi.org/10.1016/j.fuel.2006.09.006
- Mengyu, G., Deng, P., Li, M., En, Y., & Jianbing, H. (2009). The Kinetics of the Esterification of Free Fatty Acids in Waste Cooking Oil Using Fe2(SO4)3/C Catalyst. Chinese Journal of Chemical Engineering, 17, 83-87. https://doi.org/10.1016/S1004-9541(09)60037-9
- Neji, S. B., Trabelsi, M., & Frikha, M. H. (2011). Esterification of Fatty Acid over Tunisian Acid Activated Clay: Kinetic Study. Journal of Oleo Science, 60, 293-299. https://doi.org/10.5650/jos.60.293
- Ni, J., & Meunier, F.C. (2007). Esterification of free fatty acids in sunflower oil over solid acid catalysts using batch and fixed bed-reactors. Applied Catalysis A: General, 333, 122-130. https://doi.org/10.1016/j.apcata.2007.09.019
- Nuithitikul, K., Prasitturattanachai, W., & Hasin, W. (2017). Comparison in Catalytic Activities of Sulfated Cobalt-Tin and Sulfated Aluminium-Tin Mixed Oxides for Esterification of Free Fatty Acids to Produce Methyl Esters. Energy Procedia, 138, 75-80. https://doi.org/10.1016/j.egypro.2017.10.058
- Michelle, J. C., Rezende, N., & Pinto, A. C. (2016). Esterification of fatty acids using acid-activated Brazilian smectite natural clay as a catalyst. Renewable Energy, 92, 171-177. https://doi.org/10.1016/j.renene.2016.02.004
- Ozbay, N., Oktar, N., & Tapan, N. A. (2008). Esterification of free fatty acids in waste cooking oils (WCO): Role of ion-exchange resins. Fuel, 87, 1789-1798. https://doi.org/10.1016/j.fuel.2007.12.010
- Park, Y. M., Chung, S. H., Eom, H. J., Lee, J. S., & Lee, K. Y. (2010). Tungsten oxide zirconia as solid superacid catalyst for esterification of waste acid oil (dark oil). Bioresource Technology, 101, 6589-6593. https://doi.org/10.1016/j.biortech.2010.03.109
- Pasias, S., Barakos, N., Alexopoulos, C., & Papayannakos, N. (2006). Heterogeneously Catalyzed Esterification of FFAs in Vegetable Oils. Chemical Engineering and Technology, 29, 1365-1371. https://doi.org/10.1002/ceat.200600109
- Pereira, M. R. D. N., Salviano, A. B., Medeiros, T. P. V., Santos, M. R. D., Cibaka, T. E., Andrade, M. H. C., Porto, A. O., & Lago, R. M. (2018). Ca(OH)2 nanoplates supported on activated carbon for the neutralization/removal of free fatty acids during biodiesel production. Fuel, 221, 469-475. https://doi.org/10.1016/j.fuel.2018.01.123
- Pirola, C., Manenti, F., Galli, F., Bianchi, C. L., Boffito, D. C., & Corbetta, M. (2014). Heterogeneously catalyzed free fatty acids esterification in (monophasic liquid)/solid packed bed reactors (PBR). Chemical Engineering Transactions, 37, 553-558. https://doi.org/10.3303/CET1437093
- Prabhavathi, B. L. A., Gangadhar, K. N., Sai Prasad, P. S., Jagannadh, B., & Prasad, R. B. N. (2009). A Glycerol based Carbon Catalyst for the preparation of Biodiesel. ChemSusChem, 2, 617-620. https://doi.org/10.1002/cssc.200900097
- Sania, Y. M., Dauda, W. M. A. W., & Aziz, A. R. A. (2014). Activity of solid acid catalysts for biodiesel production: A critical review. Applied Catalysis A: General, 470, 140-161. https://doi.org/10.1016/j.apcata.2013.10.052
- Santacesaria, E., Tesser, R., Serio, M. D., Guida, M., Gaetano, D., & Garcia Agreda, A. (2007). Kinetics and Mass Transfer of Free Fatty Acids Esterification with Methanol in a Tubular Packed Bed Reactor: A Key Pretreatment in Biodiesel Production. Industrial and Engineering Chemistry Research, 46, 5113-5121. https://doi.org/10.1021/ie061642j
- Shah, K. A., Parikh, J. K., Dholakiya, B. Z., & Maheria, K. C. (2014). Fatty acid methyl ester production from acid oil using silica sulfuric acid: process optimization and reaction kinetics. Chemical Papers, 68, 472-483. https://doi.org/10.2478/s11696-013-0488-4
- Shanmugam, S., Viswanathan, B., & Varadarajan, T. K. (2004). Esterification by solid acid catalysts—a comparison. Journal of Molecular Catalysis A: Chemical, 223, 143-147. https://doi.org/10.1016/j.molcata.2004.02.030
- Silva, S. M., Peixoto, A. F., & Freire, C. (2018). HSO3-functionalized halloysite nanotubes: New acid catalysts for esterification of free fatty acid mixture as hybrid feedstock model for biodiesel production. Applied Catalysis A: General, 568, 221-230. https://doi.org/10.1016/j.apcata.2018.10.008
- Prasanna Rani, K. N., Prathap, K. T., Neeharika, T. S. V. R., Satyavathi, B., & Prasad, R. B. N. (2013). Kinetic Studies on the Esterification of Free Fatty Acids (FFA) in Jatropha Oil. European Journal of Lipid Science and Technology, 115, 691-697. https://doi.org/10.1002/ejlt.201200273
- Rattanaphra, D., Harvey, A. P., Thanapimmetha, A., & Srinophakun, P. (2011). Kinetic of myristic acid esterification with methanol in the presence of triglycerides over sulfated zirconia. Renewable Energy, 36, 2679-2686. https://doi.org/10.1016/j.renene.2011.02.018
- Russbueldt, B. M. E., & Hoelderich, W. F. (2009). New sulfonic acid ion-exchange resins for the preesterification of different oils and fats with high content of free fatty acids. Applied Catalysis A: General, 362, 47-57. https://doi.org/10.1016/j.apcata.2009.04.019
- Tesser, R., Casale, L., Verde, D., Di Serio, M., & Santacesaria, E. (2010). Kinetics and modeling of fatty acids esterification on acid exchange resins. Chemical Engineering Journal, 157, 539-550. https://doi.org/10.1016/j.cej.2009.12.050
- Veillette, M., Giroir-Fendler, A., & Heit, F.M. (2017). Esterification of free fatty acids with methanol to biodiesel using heterogeneous catalysts: From model acid oil to microalgae lipids. Chemical Engineering Journal, 308, 101-109. https://doi.org/10.1016/j.cej.2016.07.061
- Yadav, G. D., Asthana, N. S., & Kamble, V. S. (2003). Cesium-substituted dodecatungstophosphoric acid on K-10 clay for benzoylation of anisole with benzoyl chloride. Journal of Catalysis, 217, 88-99. https://doi.org/10.1016/S0021-9517(02)00175-6
- Yunus, N. B. M., Roslan, N. A. B., Yee, C. S., & Abidin, S.Z. (2016). Esterification of Free Fatty Acid in Used Cooking Oil Using Gelular Exchange Resin as Catalysts. Procedia Engineering, 148, 274-1281. https://doi.org/10.1016/j.proeng.2016.06.450
- Zhang, Y., Dube, M. A., Malean, D. D., & Kates, M. (2003). Biodiesel production from waste cooking oil: process design and technological assessment. Bioresource Technology, 89, 1-16. https://doi.org/10.1016/S0960-8524(03)00040-3
How to cite this article
APA
Rani, K. N. P., Neeharika, T. S. V. R., Vardhan, G. H., Kumar, T. P., & Devi, B. L. A. P. (2020). The Kinetics of the Esterification of Free Fatty Acids in Jatropha Oil using Glycerol based Solid Acid Catalyst. European Journal of Sustainable Development Research, 4(2), em0116. https://doi.org/10.29333/ejosdr/7594
Vancouver
Rani KNP, Neeharika TSVR, Vardhan GH, Kumar TP, Devi BLAP. The Kinetics of the Esterification of Free Fatty Acids in Jatropha Oil using Glycerol based Solid Acid Catalyst. EUR J SUSTAIN DEV RES. 2020;4(2):em0116. https://doi.org/10.29333/ejosdr/7594
AMA
Rani KNP, Neeharika TSVR, Vardhan GH, Kumar TP, Devi BLAP. The Kinetics of the Esterification of Free Fatty Acids in Jatropha Oil using Glycerol based Solid Acid Catalyst. EUR J SUSTAIN DEV RES. 2020;4(2), em0116. https://doi.org/10.29333/ejosdr/7594
Chicago
Rani, K. N. Prasanna, T. S. V. R. Neeharika, G. Harsha Vardhan, T. Prathap Kumar, and B. L. A. Prabhavathi Devi. "The Kinetics of the Esterification of Free Fatty Acids in Jatropha Oil using Glycerol based Solid Acid Catalyst". European Journal of Sustainable Development Research 2020 4 no. 2 (2020): em0116. https://doi.org/10.29333/ejosdr/7594
Harvard
Rani, K. N. P., Neeharika, T. S. V. R., Vardhan, G. H., Kumar, T. P., and Devi, B. L. A. P. (2020). The Kinetics of the Esterification of Free Fatty Acids in Jatropha Oil using Glycerol based Solid Acid Catalyst. European Journal of Sustainable Development Research, 4(2), em0116. https://doi.org/10.29333/ejosdr/7594
MLA
Rani, K. N. Prasanna et al. "The Kinetics of the Esterification of Free Fatty Acids in Jatropha Oil using Glycerol based Solid Acid Catalyst". European Journal of Sustainable Development Research, vol. 4, no. 2, 2020, em0116. https://doi.org/10.29333/ejosdr/7594

 Full Text (PDF)
Full Text (PDF)